М. Б. Вакарчук

Днепропетровский национальный университет

НЕКОТОРЫЕ ОЦЕНКИ КОМПЛЕКСНОЙ КУСОЧНО-ПОЛИНОМИАЛЬНОЙ АППРОКСИМАЦИИ ФУНКЦИЙ НА КРИВЫХ В ПРОСТРАНСТВЕ L_p(Г)

Важное место в теории приближения занимают вопросы, связанные с аппроксимацией функций в комплексной плоскости С. Одним из аппаратов приближения в С являются комплексные полиномиальные и аналитические сплайны, определенные впервые Дж. Албергом, Э. Нильсоном и Дж. Уолшем [1; 2]).

Пусть Г – спрямляемая жордановая кривая в комплексной плоскости С, имеющая параметрическое представление Г = {z(t) = x(t) + i y(t) : 0 ≤ t ≤ l(Г)}, где l(Г) – длина кривой, отсчитываемая от одного из ее концов. Если кривая Г – замкнутая, то в качестве точки отсчета выбирают произвольную точку на ней, считая при этом, что при возрастании t точка z(t) двигается против часовой стрелки. Полагаем z(t₁)z(t₂), если t₁<t₂, и z(t₁) z(t₂), если t₁≤t₂.

Через Ω обозначим класс кривых Г, все точки z₁ и z₂ которых удовлетворяют только одному из условий: │z₁│≤│z₂│или│z₁│≥│z₂│, если z₁z₂.

Символом Φ обозначим множество кривых, для любых двух точек которых z₁ и z₂ существует постоянная С(Г), которая зависит только от кривой Г, такая, что

l(z₁,z₂) ≤ С(Г)│ z₁–z₂│,

где l(z₁,z₂) − длина дуги c концами z₁ и z₂ (если кривая Г − замкнутая, то под l(z₁,z₂) мы будем понимать длину меньшей из дуг, на которые Г разбивается точками z₁ и z₂).

Под L_p(Г) (1≤p≤∞) понимаем пространство комплекснозначных функций f(z), заданных на кривой Г и имеющих конечную норму

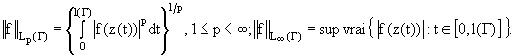
Если f(z) – комплекснозначная функция, определенная на Г, то ее производной первого порядка вдоль кривой Г в точке z(t₀) называют предел

если он существует.

Функция , заданная на кривой Г, называется абсолютно непрерывной, если почти всюду на Г существует производная и для любых

,

где а − один из концов кривой Г, если кривая не замкнутая, или произвольная точка, принадлежащая Г, если кривая замкнутая. Множество всех абсолютно непрерывных на кривой Г функций обозначим символом АС(Г).

Символом S(k,n,Г) обозначим множество кусочно-полиномиальных функций степени k−1 с n−1 свободными узлами, заданных на Г, т. е. s(z)S(k,n,Г), если существуют точки z_j=z(t_j) (j=0, 1,…,n; 0=t₀<t₁<…< l(Г)) и полиномы Q(z)P_k-1 такие, что s(z)=Q_j(z), для

Здесь P_k-1 – подпространство полиномов степени k–1. При этом s(z_n)=s(z(t_n−0)). Если кривая Г замкнутая, то полагаем z₀=z_n. Очевидно, что s(z)S(k,n,Г) является сплайном с дефектом k.

Через будем обозначать величину наилучшего приближения функции f элементами множества S(k,n,Г) в пространстве L_p(Г):

.

Приведенная ниже теорема является, в определенном смысле, обобщением на случай комплекснозначных функций ряда результатов П. Петрушева и В. Попова, установленных для функций действительного переменного [3].

Теорема. Пусть кривая Г АС(Г) и существует разбиение Г на m (m ≥1) дуг Г₁,…, Г_m, таких, что функции (k≥1) однолистны на них и кривые (j=1,…,m). Тогда для 1≤q<∞ и n=1,2,…справедливы неравенства

,

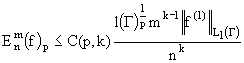где C(p,k)-константа, зависящая от указанных в скобках параметров.

Литература:

1.Ahlberg J. H., Nilson E. N., Walsh J. L. Complex cubic splines // Trans. Amer. Math. Soc. − 1967. − 129. − P. 391−413.

2.Ahlberg J. H., Nilson E. N., Walsh J. L. Properties of analitic splines // Math. Anal. Appl. − 1969. − 27. − P. 262−278.

3. Petrushev P. P., Popov V. A. Rational approximation of real function. – Cambridge: Cambridge Univ. Press., 1987. – 371 P.