Математика/ Математическое моделирование

А.М. Липанов, А.Н. Семакин

Институт прикладной механики УрО РАН

Обтекание вязким газом четырёх соприкасающихся сфер

1. Расчётная область

Рассматриваемая область представляет собой прямоугольный параллелепипед с одним входом и четырьмя выходами, в котором расположены четыре сферы, образующие пирамиду. Радиус входа – 0.5, радиус выходов – 0.35. Размеры следующие: длина – 4.0, высота – 1.81650, ширина – 1.86603. Размеры области подобраны таким образом, чтобы его боковые стенки касались образованной сферами пирамиды. Расчётная область изображена на рис. 1.

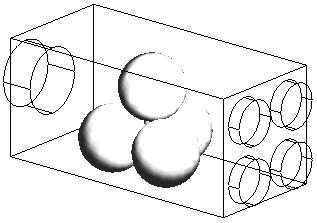
Рис. 1. Расчётная область для четырёх сфер

Сферы, составляющие пирамиду, называются по обозначению точек, в которых находятся их центры. Так, верхняя сфера называется сферой , сфера основания, касающаяся левой грани параллелепипеда, - сферой , сферы основания, касающиеся правой стенки параллелепипеда, - и , соответственно.

Поместим начало декартовой системы координат в центр тяжести треугольника с вершинами в центрах сфер основания пирамиды, ось направим в сторону выходов, ось - вверх. Тогда центры сфер имеют координаты ( - радиус сфер):

, , , .

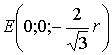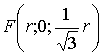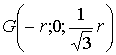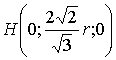На вход подаётся вязкий сжимаемый газ. Параметры течения – число Рейнольдса и , число Маха .

2. Метод решения

Для решения данной задачи используется метод конечных объёмов [1]. В [2] было показано на примере задачи обтекания сферы, что данный метод позволяет правильно моделировать поведение газа.

3. Результаты расчётов

При обтекании вязким газом пирамиды, составленной из шаров, получается следующее. При обтекании пирамиды поток с течением времени становится стационарным для обоих чисел Рейнольдса. Просто период установления при получается примерно в три раза больше. В пространстве перед пирамидой напротив входа можно выделить довольно чёткую струю газа, движущуюся по направлению к пирамиде. В нижней части этого пространства под входом располагаются два больших вихря с осью вращения, параллельной оси , которые по мере продвижения вверх по оси уменьшаются в размере, приближаются к пирамиде и отходят к боковым граням. Около верхней и нижней граней параллелепипеда вдоль лобовой поверхности сфер располагаются два вихря с осью вращения, параллельной оси . В пустое пространство внутри пирамиды газ попадает по криволинейному каналу, образованному сферами , и . Это вполне объяснимо, поскольку именно этот канал расположен по ходу движения струи. По каналу, ограниченному сферами основания , , , газ из данной области движется вниз. Одновременно газ движется в сторону выхода из пирамиды по каналам с границами, образованными сферами , , и , , .

За пирамидой располагается область, заполненная многочисленными вихрями с осями вращения, параллельными как оси , так и оси . Количество вихрей и их размеры зависит от . С ростом числа Рейнольдса количество вихрей и их интенсивность растут ( при и при в пространстве за пирамидой , где - максимум модуля завихрённости). Данная область смещена преимущественно к основанию пирамиды. В кормовом пространстве верхней сферы располагаются два вихря, вытянутые к задней грани расчётной области в виде хвоста. С ростом числа Рейнольдса данные вихри удлиняются, одновременно растёт их интенсивность.

Особо необходимо отметить, что уже при в пространстве между сферами внутри пирамиды, несмотря на его очень маленький размер, образуется несколько небольших вихрей, размеры которых сопоставимы с размером данной области (рис. 2-3).

В центре пирамиды максимальное значение скорости равно 0.8 для и 1.1 для , т.е. величина скорости имеет тот же порядок, что и при входе в объём. Давление изменяется в интервале для и для , температура - в интервале для и для .

В области перед пирамидой давление лежит в интервале при и при , после пирамиды – в интервале при и при . В выходах оно резко падает до 1.

Температура распределена по объёму более равномерно: при , при . Только при входе газа в объём наблюдается понижение его температуры.

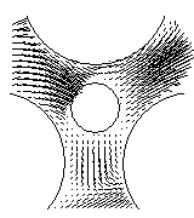
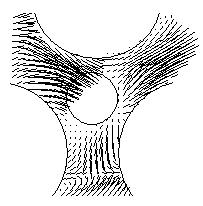
а) б)

Рис. 2. Поле скоростей в центре пирамиды в плоскости , при

а) , б)

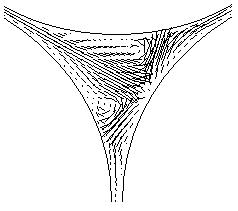
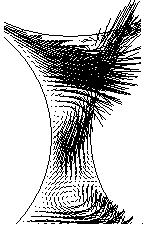
а) б)

Рис. 3. Поле скоростей в центре пирамиды при в плоскостях

а) , , б) ,

Список литературы:

1. Липанов А.М. Метод численного решения уравнений гидромеханики в многосвязных областях. //Математическое моделирование, 2006, т.18, №12, с. 3-18.

2. Липанов А.М., Семакин А.Н. Применение метода конечных объёмов к задаче обтекания сферы // Материали за 4-а международна научна практична конференция «Динамика изследования – 2008». – Т.27. Математика. Съвременни технологии на информации. Здание и архитектура. – София: «Бял ГРАД-БГ» ООД, 2008. – с. 31-35.