Карачун В.В., Мельник В.М.

Національний технічний університет України «КПІ»

ОБЧИСЛЕННЯ СИСТЕМИ АТОМАТИЧНОГО

КЕРУВАННЯ ПО МАСИВУ ОРДИНАТ ІМПУЛЬСНОЇ ХАРАКТЕРИСТИКИ ОБ’ЄКТУ

Інженерні методи дослідження систем автоматичного керування в першу чергу орієнтовані на представлення досліджуваної системи та її елементів дробово-раціональними передаточними функціями, по можливості, невисокого порядку. Це досягається шляхом ігнорування «другорядних» акумулюючих ємностей при аналітичному методі розробки математичної моделі, представленням об’єкту з суттєво вираженою розподіленістю параметрів у просторі моделлю зі скінченною кількістю зосереджених ємностей, апроксимацією експериментально визначених динамічних характеристик однією з елементарних (типових) передаточних функцій.

Таким чином, уже на стадії розробки вихідної моделі системи цілком свідомо ця модель огрублюється, з неї видаляється частина уже наявної в ній, або такої, що легко могла б бути внесена (врахована), інформації.

З ускладненням задач моделювання, з підвищенням вимог до точності результатів, які мають бути одержані в результаті моделювання, такі очікування все імовірніше стають безпідставними. «Малі» (як сподівається автор!) похибки моделі можуть до невпізнання спотворювати результат. Це особливо небезпечно, коли з моделі намагаються витиснути максимум того, на що вона здатна. А саме такі задачі в першу чергу, постають перед розробниками нових систем, заради досягнення таких результатів виконується моделювання створюваних, або систем, що підлягають автоматизації.

Вихід бачиться в урахуванні в моделі максимуму того, що відомо про об’єкт моделювання. Проблема ж ускладнення моделі при такому підході може бути скомпенсована можливостями сучасних обчислювальних машин, що слугують інструментом моделювання. Візьмемо, наприклад, об’єкти з розподіленими параметрами. Вони, як відомо, описуються диференціальними рівняннями в частинних похідних, аналітичні розв’язки яких надзвичайно громіздкі (якщо взагалі відомі математикам). Ця обставина до недавнього часу вважалась достатньою підставою «обминати» подібні моделі, зводячи їх до аперіодичної ланки з транспортним запізнюванням, ланцюжка однакових аперіодичних ланок чи чогось подібного. Але ж чисельні методи інтегрування систем диференціальних рівнянь, в тому числі рівнянь в частинних похідних на сьогодні досить добре відпрацьовані, а сучасні комп’ютери без проблем «перетравлюють» величезний обсяг обчислень, до якого зводиться таке інтегрування. Отже, обчислити, скажімо, перехідну характеристику h(t) практично будь-якого об’єкта, заданого системою диференціальних рівнянь в звичайних чи частинних похідних,- це проблема, яка, як правило, має розв’язок. Перехідна ж характеристика елементарно перераховується в імпульсну g(t)

(1)

Частотні ж характеристики каналу, для якого відома g(t), можна перерахувати за відомими формулами:

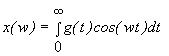; (2)

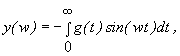(3)

де - дійсно- та уявно-частотна характеристики.

Для абсолютної більшості технологічних об’єктів в енергетиці, хімічній чи харчовій промисловості існує скінченне D, таке, що

(4)

де - наперед задана мала величина.

З урахуванням цієї обставини формули (3), (4) можна замінити на

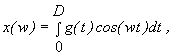(5)

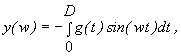(6)

А от інтеграли (5), (6) можна обчислити на комп’ютері чисельними методами. Комп’ютер зберігає інформацію про g(t) у вигляді масиву, скажімо, типу

type CoefL=array[-1..600] of real

з кроком Dt за часом між сусідніми ординатами g(t), наприклад за схемою

	-1	0	1	2	3	...	L	L+1	...	600
Mg	L	g0	g1	g2	g3	...	gL	Dt

Тут

Якщо скористатись методом трапецій для обчислення інтегралів (5), (6), то

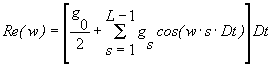(7)

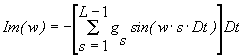(8)

Тут вважаємо, що

Але формули (7), (8) дають прийнятну точність, коли в періоді T, що відповідає частоті , тобто поміщається, принаймні, , тобто за умови

(9)

або, що теж саме

(10)

А що робити, коли більша, ніж це дозволяє умова (10)? Масив Mg треба «ущільнити», тобто перерахувати його на менший крок, ну, скажімо на крок DtW, який одержимо шляхом модифікації умови (9)

звідки

(11)

Перерахунок масиву Mg з кроку Dt на крок DtW можна виконати шляхом лінійної чи будь-якої інтерполяції, або, краще, за допомогою кубічного сплайна, який попередньо формується на базі масиву Mg або ж масиву, одержаного із Mg шляхом «проріджування», коли масив Mg надто довгий. «Проріджування» (вибірка кожного k-го, наприклад), як правило, не призводить до значного огрублення g(t), коли g(t) має відносно нескладну форму, що характерно для високоінерційних,. неколивних технологічних об’єктів.

Описаний алгоритм обчислення окремої точки амплітудно-фазової характеристики W(jw)=X+jY (для заданого значення частоти w) оформимо на Турбо-Паскалі у вигляді підпрограми

Procedure UrGod;

var s:integer; Wt,Dtw,g,r:real;

begin

x:=G[0]/2; Y:=0;

if W<=Pi/(10*Dt)

then

begin

for s:=1 to L-1 do

begin Wt:=W*s*Dt; g:=Mg[s]; X:=X+g*cos(wt); Y:=Y-g*sin(wt) end;

X:=X*Dt; Y:=Y*Dt

end

else

begin

Dtw:=Pi/(10*W); Lw:=round(D/Dtw); Dts:=D/Lw;

for s:=1 to Lw-1 do

begin

Wt:=W*S*DtW; g:=Splint(s*Lspl/Lw);

X:=X+g*cos(Wt); Y:=Y-g*sin(Wt)

end;

X:=X*Dtw; Y:=Y*Dtw

end;

if Syst then

case Nzr of

1:begin X:=X*Kreg; Y:=Y*Kreg end;

2:begin r:=Y*Kreg/w; Y:=-X*Kreg/w; X:=R end;

3:begin

R:=Kreg*(X-Y*Tv*w); Y:=Kreg*(Y+X*Tv*w); X:=r

end;

4:begin

r:=Kreg*(X+Y/(Ti*w)); Y:=Kreg*(Y-X/(Ti*w)); X:=r

end;

5: begin

r:=Kreg*(X-y*(Tv*w-1/(Ti*w)));

Y:=Kreg*(Y+X*(Tv*W-1/(Ti*w))); X:=r

end

end

end;

В цій підпрограмі масив Mg, змінні X,Y,w,Dt,D типу real, а також Syst (типу boolean), Nzr (типу integer), Kreg,Ti,Tv (типу real) - глобальні параметри. Параметр Syst=true , якщо розраховується точка амплітудно-частотної характеристики розімкненої системи, і Syst=false, коли мова йдеться про точку амплітудно-фазової характеристики об’єкта. Nzr - номер закону регулювання (прийнято, що Nzr=1 відповідає П(пропорційному) регулятору, Nzr=2 - інтегральному (І), Nzr=3 - пропорційно-диференціальному (ПД), Nzr=4 - ізодромному (ПІ) і, нарешті, Nzr=5 - ПІД - регулятору. Підпрограма Splint реалізує сплайнову інтерполяцію функції g(t) .

Отже, процедура UrGod дозволяє розраховувати як частотні характеристики об’єкта, так і розімкненої системи з одним із перелічених вище типових лінійних регуляторів.

Остання обставина дозволяє розв’язувати проблему дослідження стійкості замкненої системи (через критерій Найквіста), проблему настройки замкненої системи на заданий покажчик коливності, задачі в межах методу гармонічної лінеаризації і цілий ряд інших задач, наприклад, визначення частоти зрізу неперервної частини цифрових систем і таке ін.

Перехідні процеси в замкненій системі можна обчислювати або добавляючи до математичної моделі об’єкта керування диференціальне рівняння регулятора (та, можливо, інших елементів, необхідних для замикання системи, як-то датчиків, виконавчих механізмів, ліній передач, тощо) і потім крок за кроком послідовно чисельно інтегруючи одержану систему рівнянь, або ж використовуючи інтеграл згортки для обчислення реакції об’єкта на послідовність імпульсів, на які розкладається вихідний сигнал регулятора, і використовуючи масив ординат імпульсної характеристики об’єкта.

Отже, і перехідні процеси можна обчислювати через g(t), використовуючи g(t), одержане з максимальною доступною точністю (можливо, експериментально), не витрачаючи час на апроксимацію і не огрублюючи модель об’єкта, отже, не ризикуючи непередбачуваними похибками, що можуть виникнути в процесі такої апроксимації.