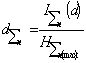A MATHEMATICAL INTERPRETATION OF INFORMATION ANALYSIS OF TECHNOLOGICAL PROCESSES

S.Sh.Kazhikenova, M.Kalikbergenova

Quantitative estimations of sense and value of the information can be made for the information analysis of quality of technological products and processes of their reception only after the preliminary agreement about what precisely in each concrete case has value and sense for the considered phenomena. Methods of calculation the information suggested by Shannon allow to reveal a ratio of quantity of the predicted information and quantities of the unexpected information which cannot be predicted beforehand, and thus to enable to define a qualitative and quantitative estimation of the certain technological circuit. As a probability of detection of the main element of technological system it is possible to accept its maintenance in a product, expressed in shares of unit. For example, let’s examine the maintenance of a considered chemical element, in our case - copper, in products of technological repartition. Also for probability of detection it is possible to take the maintenance of suitable fraction (remnants, briquettes) in a corresponding product. The same concerns the process of extraction of an element in this or that product, as in this case a parameter of extraction is equal to a probability of transition of the given element from one condition of system into another. These both parameters - the maintenance and extraction - can be equally used for an estimation of quality of a product or technological repartitions.

Let's show how quality of technological products and the technological processes resulting in reception of these products is estimated by results of technological repartitions copper-liquating manufactures on Zhezkazgan and Balkhash copper-smelting plants (CSP) (table 1). So, the maintenance of copper in ore makes 0,5-1,2% (on the average 0,85%), and in concentrates 5,5-40% (on the average 22,75%). Stein of melting in a liquid bath contains 40-55% copper (on the average 47,5%) . The basic result of the work carried out on a scientific, technological and technical substantiation of process of converting finally is reduced to an opportunity to increase the maintenance of copper in draft metal.

Table 1 - The maintenance of copper in products on Zhezkazgan and Balkhash CSP

Repartition	The name	Maintenance	Average value
Extraction	Ore	0,5-1,2%	0,85%
Enrichment	A concentrate	5,5-40%	22,75%
Melting	Stein	40-55%	47,5%
Converting	Draft copper	98,6-98,9%	98,75%
Fire refinement	Anodic copper	99,2-99,5%	99,35%
Electrolyte refinement	Cathode copper	99,9-99,99%	99,95%

This parameter varies within the limits of 98,6-98,9% (on the average 98,75%). As a result of technological process of anodic melting the parameters of the maintenance of copper in anodes are the following 99,2-99,5% (on the average 99,35%). In process of electrolyte refinements parameters of the maintenance of copper in cathodes make 99,9-99,99% (on the average 99,95%).

For accounting of a various degree of unexpectedness (probability) of events K. Shannon has suggested to use probabilities' function of entropy borrowed from statistical physics, resulted as follows:

,

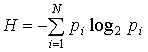where – is a probability of detection of any homogeneous element of system in their set , , .

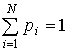If is a probability of detection of a controllable element then unexpectedness or uncertainty of this detection is equal to . In our variant of estimation this uncertainty will be expressed as:

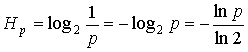. (1)

Before the publication of K. Shannon's theory R.Hartly has suggested to define quantity of the information under the formula:

, (2)

where , - number of levels, - length of a code of elements at each level of hierarchical system.

The theorem 1 Let - number of elements of - level. - capacity of the information of a zero level of technological system. Then the capacity of the information of -level counting upon one element is expressed by the formula:

.

In the technological circuit considered by us there is a sample of set of elements - an element and not an element (in our case copper and all other elements in aggregate) then the equation (2) will become:

.

On the basis of the theorem 1 we shall calculate the maximal information of the technological circuit on initial 10 levels at :

0 1 2 3 4 5 6 7 8 9 10

, 1 2 4 8 16 32 64 128 256 512 1024

bit/el.

Essentially important advantage of an information estimation of quality of products or technological operations is that a suggested parameter , as well as any entropy-information sizes, can be added. The given property of additive is immanently inherent to entropy and information and is a basis for expression of the law of preservation of their sum. Hence, technological uncertainty of various operations within the limits of the unified circuit can be expressed by a system parameter of uncertainty:

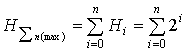, bit/el.

Or for initial 10 levels:

0 1 2 3 4 5 6 7 8 9 10

, 1 3 7 15 31 63 127 255 511 1023 2047

bit/el.

The theorem 2 Information capacity of hierarchical system and n-level are defined by equality:

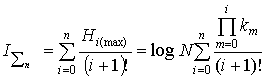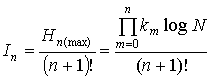, , (3)

where - greatest possible entropy of a system.

The determined component of the information on the basis of the theorem 2 is defined by equality:

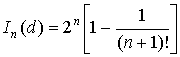bit/el.

0 1 2 3 4 5 6 7 8 9 10

, 0 1 3,33 7,67 15,9 32,0 64,0 128 256 512 1024

bit/el.

As the information capacity of technological system is defined by its stochastic part on the basis (3) we shall receive:

0 1 2 3 4 5 6 7 8 9 10

, 1 1 0,6667 0,3333 0,1333 0,0444 0,0127 0,0032 0,0007 0,0001 0,0000

bit/el.

The system determined component is equal:

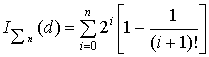bit/el.,

0 1 2 3 4 5 6 7 8 9 10

, 0 1 4,33 12 27,9 59,8 124 252 508 1020 2044

bit/el.

Having defined degrees of determination and ineradicable stochasticity at each level of technological system under formulas:

, ,

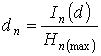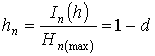let's analyze the received results of the carried out calculations which are submitted in table 2.

Table 2 - Settlement information-entropy characteristics of technological repartitions in hierarchical system for ,

0	0	1,0	0	0	1,0	0
1	1,00	2,0	0,50	1,00	3,0	0,33
2	3,33	4,0	0,83	4,33	7,0	0,62
3	7,67	8,0	0,96	12,0	15,0	0,80
4	15,9	16,0	0,99	27,9	31,0	0,90
5	32,0	32,0	1,0	59,8	63,0	0,95
6	64,0	64,0	1,0	124,0	127,0	0,98
7	128,0	128,0	1,0	252,0	255,0	0,99
8	256,0	256,0	1,0	508,0	511,0	0,99
9	512,0	512,0	1,0	1020,0	1023,0	0,998
10	1024,0	1024,0	1,0	2044,0	2047,0	0,999

We shall illustrate the comparison of these data with practical "know-how" of copper (tab. 1) graphically in coordinates . The factor of their correlation has made 0, 8614 at the importance 6, 6744 that testifies the adequacy of suggested model of an information estimation of quality of products in consecutive operations of the technological circuit.

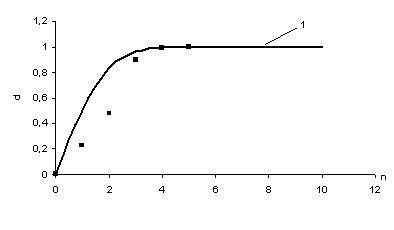
1 - dependence on new model, points - experimental data

Figure 1 - Dependence of a degree of determination on a level

The size in this case does not influence the solution of a problem as it is reduced at calculation of level 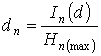and system 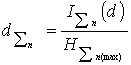determinations

Thus, the theorems proved in the given section show indissoluble connection of the determined and stochastic components from which the first is dominating and providing stability, and the second defines the most thin changes and optimum information capacity of technological systems. In this connection we conclude, that the entropy-information approach to research of technological systems is objectively necessary.