К.ф.-м.н Билюк А.И., Билюк А.А., Холод А.П ., Красна Л. М., Витюк А. В.

ПОХИБКА ЕКСПЕРИМЕНТУ ПРИ ВИМІРЮВАНІ СПЕКТРІВ РОЗСІЮВАННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ В МЕТАСТАБІЛЬНИХ СИСТЕМАХ

Застосування методу механічної спектроскопії (МС) для дослідження дефектної структури речовини дає можливість більш повно зрозуміти процеси, що протікають в ній. Але більшість результатів, які отримані цим методом на сьогоднішній день, носять якісний характер. Такий стан речей пояснюється тим, що отримані спектри розсіювання непружної енергії не мають однозначного трактування. Особливо це стосується явищ, які спостерігаються при дослідженні метастабільних структур, коли можлива рухливість дефектних утворень. В таких випадках математична обробка експерименту вимагає особливої ретельності.

Якщо отримані залежності МС від зовнішніх впливів носять відомий характер, тобто до них можна застосувати якусь гіпотезу, то при розрахунку коефіцієнтів, які включають в себе структурні параметри, застосовується метод найменших квадратів. Але в багатьох випадках гіпотеза поведінки невідома. Тоді необхідно проводити аналіз точності кожного вимірювання величини МС в експерименті, що проводиться.

Головна мета при розробці установок для дослідження МС - це досягти мінімальний рівень апаратних втрат в системі. Останні викликані втратами енергії в матеріалі елементів конструкції, механічним тертям в затискачах зразка і тертям рухомих систем з навколишнім середовищем [1], тобто:

(1)

де ΔQ_з^-1 - втрати в затискачах; ΔQ_нс^-1 - втрати при терті з навколишнім середовищем; ΔQ_к^-1 - втрати в матеріалі конструкції. Тобто похибка методу складається із похибок, які вносяться установкою ΔQ_у^-1 і самим методом вимірювання ΔQ_в^-1.

Для зменшення фонових втрат розсіювання енергії в конструкції і знаходження оптимальних умов її експлуатації використаємо метод математичного планування [2,3]. В якості параметра оптимізації авторами був вибраний фон МС при 20⁰C (Q_ф^-1). Вивчали вплив наступних факторів на рівень МС:

1) x₁ - відношення мікротвердості затискача і зразка;

2) x₂ - відношення жорсткості стержня до жорсткості зразка (k_ст/k_зр) (k=(π·d⁴·G)/(32·l), де - G -модуль зсуву, d - діаметр, l - довжина);

3) x₃ - відношення жорсткості нитки до жорсткості зразка (k_н/k_зр).

Для всіх факторів на основі апріорних даних вибрали нульовий рівень та інтервали варіювання.

В результаті проведеного факторного експерименту обчислили коефіцієнти рівняння регресії. Одержане авторами рівняння має вигляд (Q_ф^-1 = y):

(2)

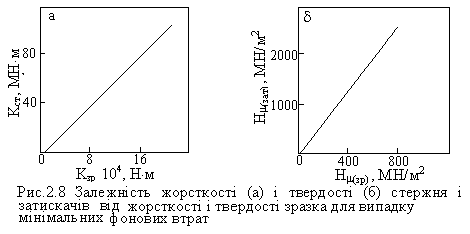
На основі одержаної математичної моделі процесу побудували номограми (рис.1), за допомогою яких можна визначити параметри конструкції приладу. Так, знаючи мікротвердість зразка і обчисливши його жорсткість, по номограмі визначається мікротвердість затискачів і жорсткість стержня. Апаратні втрати при цьому будуть мінімальні. Для крутильного маятника рекомендовано вибирати таку систему затискачів, щоб виконувалось співвідношення [3]: {k_ст./k_зр.}>100.

Крім цього, джерелом значних систематичних похибок можуть бути аеродинамічні втрати, які є функцією густини середовища і форми деталей рухомої системи. Згідно підрахунків, які зроблені в роботі [1], аеродинамічні втрати в системах типу крутильного маятника складають:

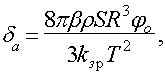(3)

де β - коефіцієнт опору, який при малих швидкостях є функцією числа Рейнольдса; ρ- густина навколишнього середовища; S - поперечний переріз стержня, який нормальний до напрямку швидкості його руху; R - половина довжини інерційної штанги; φ_o - максимальний кут закручування; T - період коливань; k_зр - жорсткість зразка.

Підрахунки показали, що ці втрати зменшуються із зростанням частоти коливань і збільшуються пропорційно амплітуді деформації. Найбільш ефективне зменшення аеродинамічних втрат досягається при вимірюванні ВТ в вакуумі і зменшується до нуля при залишковому тиску нижче 1 Па.

ЛІТЕРАТУРА

1. Постников В.С. Внутреннее трение в металлах. - М.: Металлургия, 1974. -352с

2. Адлер Ю.П. Планирование эксперимента при поиске оптимальных условий./ Ю.П. Адлер, Е.В. Маркова, Ю.В. Грабовский. - М.: Наука, 1978. -279с.

3. Білюк А.І. Вплив термоциклювання в полях зовнішніх напружень на формування і стабілізацію структури дисперсійно-твердіючих сплавів// Чернівецький державний університет: Авториферат дисертації на здобуття наукового ступеня кандидата фізико-математичних наук. – Чернівці, 1997.-19с.