Котов Д. В.

Национальный Технический Университет Украины «Киевский Политехнический Институт»

Модель поляризации рутила в диапазоне СВЧ

Рутил (TiO₂) является диэлектриком, который, благодаря высокому значению диэлектрической проницаемости, широко используется в электронике СВЧ и он является основой для многих СВЧ диэлектриков. К сожалению, на данный момент характеристики современных СВЧ диэлектрических материалов с высокой диэлектрической проницаемостью не могут быть детально объяснены с теоретической точки зрения. Понимания явлений поляризации в диэлектриках, а, отсюда, термостабильности диэлектрической проницаемости и диэлектрических потерь даст в дальнейшем возможность создания более качественных материалов с лучшими показателями.

Для создания модели поляризации рассмотрим следующую задачу и проверим ее корреляцию со свойствами рутила. Допустим, что у нас есть точечный заряд в единичном объеме с некоторой диэлектрической проницаемостью ε, на который действует внешнее электрическое поле Е. Под действием поля заряд отклоняется на некоторую величину r от точки равновесия. Это приводит к возникновению электрического момента p=q∙r. Рассмотрим эту структуру с макроскопической стороны. Под действием электрического поля в этом объеме возникает поляризованность P:

(1)

где χ – электрическая восприимчивость.

Поляризованность также описывается через микроскопические величины, такие как поляризация:

(2)

где F – микроскопическое поле, которое влияет на заряд, α – поляризация.

Знак суммы объясняется вкладом нескольких механизмов поляризации. В данном случае присутствует всего один механизм поляризации. Рассмотрим величину поляризации через электрический момент:

(3)

Подставив выражение (3) в (2) и прировняв его к выражению (1), получим:

(4)

Выразив значение χ из формулы (4), получим:

(5)

Как известно, диэлектрическая восприимчивость может быть выражена через диэлектрическую проницаемость χ=ε-1. Подставив значение χ в выражение (4), выразив значение χ из формулы, получим:

(5)

Пусть есть две среды a и b с разной диэлектрической проницаемостью, одинаковым точечным зарядом, электрическим полем и концентрацией. Тогда по формуле (5) мы получим соотношение:

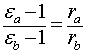(6)

Если значение ε>>1 тогда формула (6) упрощается:

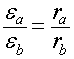(7)

Для дальнейшей проверки данного соотношения на материалах, нужно задать некоторые критерии. В первую очередь, материал должен быть анизотропным. Также его магнитная проницаемость должна быть равна 1, так как при анализе зависимости ее значение бралось 1, как очевидное, чтобы исключить магнитную зависимость. Данным условием хорошо соответствует рутил с хорошо выраженной анизотропией в СВЧ диапазоне.

Рассмотрим кристаллическую структуру рутила. Она представляет собой оксидные октаэдры, внутри которых находятся ионы титана. Колебания титана в октаэдре можно представить в виде эллипсоида с максимальным объемом, который вписан в октаэдр. То есть отклонением элементарного заряда в очень малом объеме есть значение расстояния титана от центра равновесия к поверхности эллипсоида в кристаллофизических направлениях. Значения отклонений, судя по элементарной ячейке, будут отличаться по осям x и z. Судя с диэлектрических данных по рутилу [1], именно в этих направлениях отличаются значения диэлектрической проницаемости. За осью x диэлектрическая проницаемость соответствует значению 80, тогда как за осью z равна 170. Расчет максимального отклонения заряда в октаэдре рассчитывается за счет расчета размеров вписанного эллипсоида и расчета расстояния от его центра до его же крайних точек поверхности по кристаллофизическим осям. Используя значения расстояния между ионами в рутиле [2], можно рассчитать значения этих расстояний: 0,66 и 1,175 ангстрем по оси x и z соответственно.

Применив формулу (7), сравним отношения диэлектрических проницаемостей и расстояний максимального отклонения от точки равновесия:

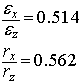(8)

Учитывая погрешности размеров элементарной ячейки, диэлектрических проницаемостей, можно считать, что соотношения диэлектрических проницаемостей коррелируют с отношением максимальных отклонений от положения равновесия. Так как данное соотношение (7) выполняется, то можно считать, что титан в СВЧ диапазоне является точечным зарядом, который колеблется в кислородном октаэдре. Так же объясняется и отрицательный ТКε рутила. При нагреве, колебания кислорода в структуре увеличивают свою амплитуду и , таким образом, противодействуя колебанию точечного титана, уменьшая его амплитуду колебаний и, соответственно, диэлектрическую проницаемость.

Литература

1. Ю. М. Поплавко, В. І. Молчанов, В. А. Казміренко Мікрохвильова діелектрична спектроскопія, - К.: НТУУ «КПІ» 2011. – 304 с.

2. F. A. Grant/ Properties of Rutile (Titanium Dioxide)// Reviews of modern physics, V. 31, N. 3, 647-674.