Строительство и архитектура / 3.Современные технологии строительства, реконструкции и реставрации.

аспирант Шехоркина Н.Е.

Государственное высшее учебное заведение «Приднепровская государственная академия строительства и архитектуры», г. Днепропетровск, Украина

Разработка аналитического метода определения параметров инъектирования и характеристик основания после закрепления

Введение. В статье представлены материалы теоретических исследований процесса инъектирования песчаного основания, направленные на определение напряженно-деформированного состояния грунтовых оснований в процессе их инъектирования и выявление зон предельного состояния с учетом наличия пластических зон в сферической системе координат. Предложены математические зависимости и разработан метод, позволяющий определить основные технологические параметры инъектирования – радиус распространения раствора и давление нагнетания с учетом глубины инъектирования и характеристик основания природного сложения, а также характеристики грунта после закрепления.

Ключевые слова: инъектирование, расширяющаяся полость, итерационный метод, радиус распространения раствора, давление нагнетания, характеристики основания.

Изложение основного материала исследований. При нагнетании цементного раствора в скважины и полости происходит расширение выемок в грунте с последующим его уплотнением. Определение напряжений на границе скважины и перемещений стенок скважины можно отнести к классической задаче Ламе об определении напряжений и перемещений стенок в осесимметричных толстостенных сосудах.

Все известные подходы [1 – 5] к аналитическому решению задачи расширения полости используют следующие допущения, которые позволяют свести рассматриваемую задачу к одномерной. Грунт рассматривается как упругопластическая полностью однородная среда со своими физико-механическими свойствами и гидростатическое давление, действующее во всем массиве грунта, одинаково. 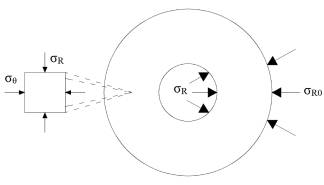Напряженно-деформированное состояние грунта (НДС) вокруг расширяющейся полости в этом случае удобно рассматривать в сферической системе координат и характеризовать радиальными σ_R и тангенциальными σ_θ компонентами напряжений и радиальными смещениями материальных точек u. Начальное напряженное состояние до расширения полости представляется σ_R0. Схематически задача о расширяющейся полости в сплошной среде представлена на рис. 1.

а)

б)

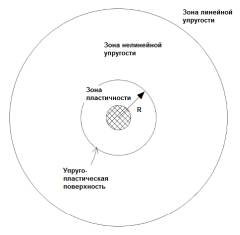
Рис. 1. Задача о расширяющейся полости: а) схема действующих напряжений; б) зоны деформаций

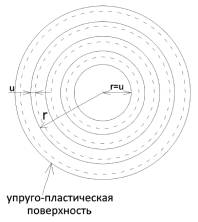
Для определения предельно допустимого значения давления инъектирования, радиуса распространения раствора и характеристик основания после усиления разработан итерационный метод. Основную идею разработанного метода можно сформулировать так: грунтовая среда разбивается на n элементарных колец с некоторым радиусом r (рис. 3.3), предполагая, что в пределах каждого элементарного кольца среда изотропна. Число элементов назначается в зависимости от требуемой точности решения. Пунктирной линией на рис. 2 изображено начальное положение частиц грунта до образования полости, сплошной – после начала образования полости. Разница между начальным и конечным радиусом представляет собой перемещение частиц u. По мере перехода от одного элементарного кольца к другому по направлению к центру скважины разница между радиусом кольца r и перемещением частиц u постепенно уменьшается до их равенства у стенок полости (r → u). На этом этапе процесс итерации с определением напряжений, перемещений и характеристик грунта на каждом этапе завершается.

а)

б)

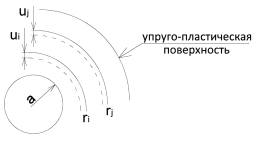
Рис. 2. К методу определения параметров инъектирования и характеристик основания после усиления: а) схема разбивки грунтовой среды на элементарные кольца; б) радиусы и перемещения внешней и внутренней граней элементарного кольца

Разработанный метод для наглядности представлен в виде законченного алгоритма с учетом всех действий, необходимых для обеспечения его работоспособности и реализован в ПК MathLab. Блок-схема алгоритма приведена на рис. 3.

Блок-схема алгоритма включает в себя три блока итерационных процедур: «Блок расчета 1» (рис. 4), «Блок расчета 2» (рис. 5), «Блок расчета 3» (рис. 6).

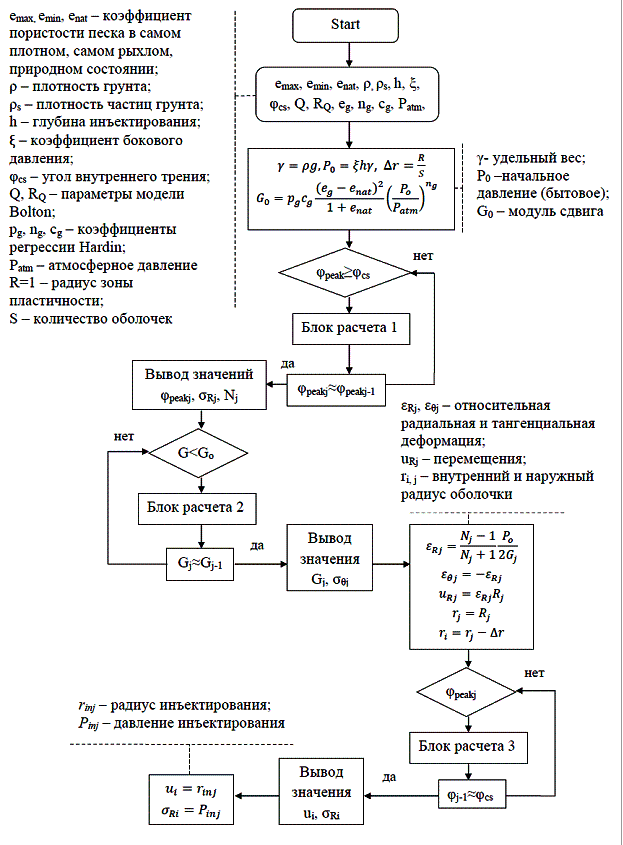
Рис. 3. Блок-схема алгоритма итерационного метода расчета параметров инъектирования и характеристик основания после закрепления

Суть итерационного процесса «Блок расчета 1» (рис. 4) заключается в определении значений угла внутреннего трения φ_peakj, радиальных напряжений σ_Rj, коэффициента напряжений при разрушении N_j на упруго-пластической поверхности. Для этого в начале итерационного процесса задается начальное (предполагаемое) значение угла внутреннего трения φ_peak, которое превышает значение угла внутреннего трения φ_cs грунта природного сложения, поскольку за счет сдвигов в зоне пластичности произойдет дополнительное уплотнение грунта. Расчет заканчивается, когда разность между значениями угла внутреннего трения предыдущего и последующего решения составляет для каждого элементарного кольца не более 0,005.

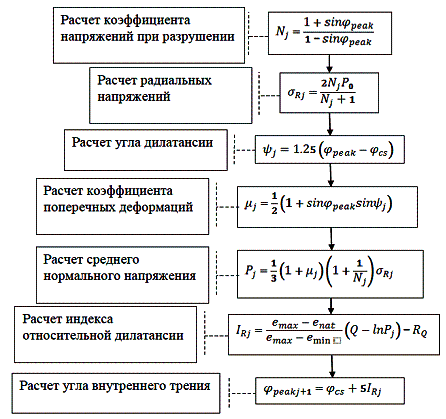
Рис. 4. Блок-схема процедуры «Блок расчета 1»

Для определения напряжений и перемещений на упруго-пластической поверхности необходимо определить соответствующее значение модуля сдвига G, которое зависит от перемещений в нелинейно упругой зоне. С этой целью выполняется итерационный процесс «Блок расчета 2» (рис. 5). В начале процедуры принимается значение модуля сдвига G < G₀. Расчет прекращается, когда разность между значениями модуля сдвига предыдущего и последующего решения составляет для каждого элементарного кольца не более 0,005.

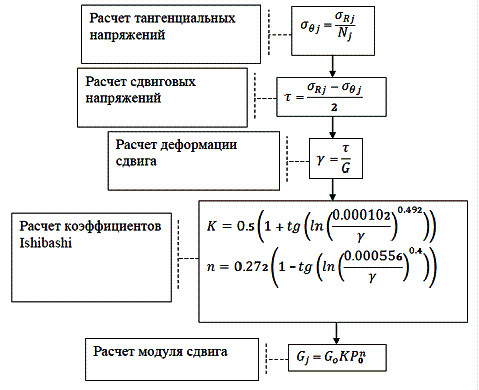
Рис. 5. Блок-схема процедуры «Блок расчета 2»

Таким образом, выполняя процедуры «Блок расчета 1» и «Блок расчета 2», определяются значения радиальных и тангенциальных напряжений и относительных деформаций, перемещения, модуля сдвига и угла внутреннего трения на упруго-пластической поверхности (наружный радиус элементарного кольца). В алгоритме величины, рассчитанные для наружного радиуса элементарного кольца, снабжены индексом «j», для внутреннего радиуса – «i».

С целью определения вышеуказанных величин на внутреннем радиусе элементарного кольца выполняется итерационный процесс «Блок расчета 3» (рис. 6).

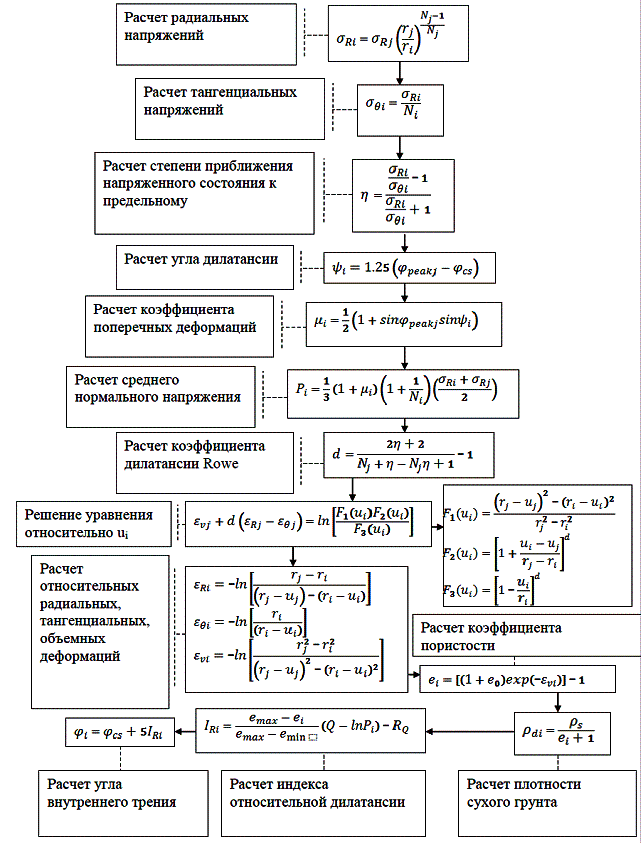
Рис. 6. Блок-схема процедуры «Блок расчета 3»

Процесс итерации процедуры «Блок расчета 3» прекращается, когда разность между значениями угла внутреннего трения φ_j-1 и угла внутреннего трения φ_cs грунта природного сложения составляет не более 0,005. При этом радиус распространения раствора и предельно допустимое давление нагнетания раствора равны соответственно значениям перемещения и радиальному напряжению, полученным на последнем шаге расчета.

Выводы. Применительно к песчаным грунтам разработан метод определения технологических параметров процесса инъектирования грунтовых оснований, позволяющий определять предельно допустимое давление и радиус инъектирования, а также характеристики упрочненного основания.

Литература

1. Гревцев А. А. Теория расширения полости и предельное сопротивление грунта под нижним концом забивных свай в песчаных грунтах / А. А. Гревцев, В. Г. Федоровский // Жилищное строительство. – 2012. – № 9. – С.2-5.

2. Полищук А. И. Условия формирования зоны предельного уплотнения вокруг ствола инъекционной сваи в слабых глинистых грунтах / А. И. Полищук, Р. В. Шалгинов, С. П. Осипов // Вестник ТГАСУ : сб. науч. тр. – Томск, 2007. – Вып. 3. – С. 173-185.

3. Ishibashi I. Unified dynamic shear moduli and damping ratios of sand and clay / I. Ishibashi, X. Zhang // Soils and foundations. – 1993. – Vol. 33(1). – P. 181-191.

4. Salgado R. Cavity expansion and penetration resistance in sand / R. Salgado, J. K. Mitchell, M. Jamiolkowski // Journal of geotechnical and geoenvironmental engineering. – 1997. – Vol. 123 (4). – P. 344-354.

5. Yu H. S. Finite cavity expansion in dilatant soils / H. S. Yu, G. T. Houlsby. – Режим доступа: http://www.eng.ox.ac.uk/civil/publications/reports-1/ouel_1905_91.pdf.