Сизоненко В.Л.
Харьковский национальный
аграрный университет имени В.В. Докучаева
К теории пучково-плазменной неустойчивости
В работах [1], [2]
показано, что при взаимодействии холодных пучков плазмы со стохастическими
электрическими полями ![]() , состоящими из разделенных в пространстве волновых пакетов со случайными
фазами, происходит полное торможение пучков с переходом до 50 % их энергии в
температуру электронов плазмы. Такой характер плазменно-пучковых взаимодействий
кардинально отличается от случая возбуждения пучками монохроматических волн,
когда в плазму переходит лишь небольшая часть кинетической энергии пучков [3] –
[6].
, состоящими из разделенных в пространстве волновых пакетов со случайными
фазами, происходит полное торможение пучков с переходом до 50 % их энергии в
температуру электронов плазмы. Такой характер плазменно-пучковых взаимодействий
кардинально отличается от случая возбуждения пучками монохроматических волн,
когда в плазму переходит лишь небольшая часть кинетической энергии пучков [3] –
[6].
По-другому
взаимодействуют с плазмой первоначально горячие пучки частиц, для которых
справедливо условие ![]() , т.е.
, т.е. ![]() , где
, где ![]() и
и ![]() – плотности частиц пучка и
электронов плазмы соответственно,
– плотности частиц пучка и
электронов плазмы соответственно, ![]() – направленная скорость пучка,
– направленная скорость пучка, ![]() – его тепловая скорость
– его тепловая скорость ![]() . При этом система уравнений для усредненных характеристик электронов пучка
и плазмы при их взаимодействии со стохастическими электрическими полями была
получена в [2], и имеет следующий вид:
. При этом система уравнений для усредненных характеристик электронов пучка
и плазмы при их взаимодействии со стохастическими электрическими полями была
получена в [2], и имеет следующий вид:
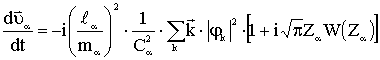 , (1)
, (1)
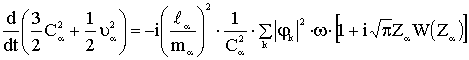 , (2)
, (2)
где ![]() и
и ![]() – средняя и тепловая скорости
частиц сорта
– средняя и тепловая скорости
частиц сорта ![]() (
(![]() = 0; 1 – электроны плазмы, пучка),
= 0; 1 – электроны плазмы, пучка), ![]() – массы частиц,
– массы частиц, ![]() – Фурье-компонента потенциала
– Фурье-компонента потенциала ![]() ,
, ![]() и
и ![]() – комплексная частота и волновой
вектор электрического поля,
– комплексная частота и волновой
вектор электрического поля, ![]() ,
, ![]() – функция Крампа:
– функция Крампа:
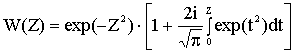 .
.
Дисперсионное уравнение для колебаний
электрического поля в нелинейном режиме было выведено из уравнения Пуассона
[2]:
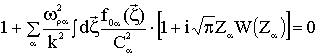 , (3)
, (3)
где ![]() – функция распределения по
начальным (в момент
– функция распределения по
начальным (в момент ![]() ) скоростям частиц
) скоростям частиц ![]() ,
, ![]() .
.
Полагая в (3) ![]() ,
, ![]() , и
, и
![]() , (4)
, (4)
получим известное [7] –
[9] дисперсионное уравнение линейной теории
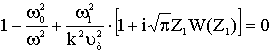 , (5)
, (5)
где ![]() . В случае (
. В случае (![]() ) из (5) находим следующие значения частоты
) из (5) находим следующие значения частоты ![]() и инкремента
и инкремента ![]() :
:
![]() ;
; 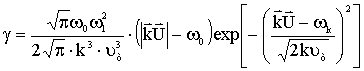 . (6)
. (6)
Для этой неустойчивости
механизм квазилинейной теории торможения пучка изучен достаточно полно [10].
Вместе с тем, сама квазилинейная теория вызывает возражения по той причине, что
в ней осциллирующая часть функции распределения частиц берется без учета
нелинейных слагаемых уравнения Власова, которые содержат секулярности.
Положение не спасает и теория уширения резонансов ![]() , развитая в [11] – [14], поскольку и она является
феноменологической, а не точной. В нашей же теории стохастических процессов
феноменологии нет.
, развитая в [11] – [14], поскольку и она является
феноменологической, а не точной. В нашей же теории стохастических процессов
феноменологии нет.
В одномерном приближении
частота колебаний в нелинейном режиме определяется формулой (6), а для
инкремента из (3) будем иметь, что
![]() , (7)
, (7)
где ![]() ,
,
![]() .
.
Величины ![]() и
и ![]() зависят от начальной
скорости частиц
зависят от начальной
скорости частиц ![]() . С течением времени они меняются, оставаясь функциями
. С течением времени они меняются, оставаясь функциями ![]() . При этом выражению
. При этом выражению ![]() в момент
в момент ![]() соответствует (равно)
некоторое выражение
соответствует (равно)
некоторое выражение ![]() , где неизвестная пока функция
, где неизвестная пока функция ![]() удовлетворяет
равенству
удовлетворяет
равенству
![]() , (8)
, (8)
а при ![]() справедливо условие:
справедливо условие: ![]() . Тогда инкремент (7) можно записать так
. Тогда инкремент (7) можно записать так
![]() . (9)
. (9)
Далее будем считать
величину ![]() некоторой функцией
некоторой функцией ![]() и
и ![]() :
: ![]() , что соответствует зависимости
, что соответствует зависимости ![]() , если
, если ![]() выразить через
выразить через ![]() .
.
Если ![]() , то условие
, то условие ![]() выполняется при
выполняется при ![]() . Полагая далее
. Полагая далее ![]() и раскладывая
и раскладывая ![]() и
и ![]() по малым значениям
по малым значениям ![]() (это условие
проверяется позже верификацией), из (7) будем иметь после интегрирования по Z,
что
(это условие
проверяется позже верификацией), из (7) будем иметь после интегрирования по Z,
что
![]() . (10)
. (10)
Заметим, что при этом
величина ![]() и её производные по
и её производные по ![]() из (10) выпадают.
из (10) выпадают.
Интегрируя далее
равенство
![]()
слева по ![]() , а справа по
, а справа по ![]() , получим, что
, получим, что
![]() , (11)
, (11)
где ![]() – функция Лапласа.
Поскольку левая часть (11) не зависит от времени, то, дифференцируя её по
– функция Лапласа.
Поскольку левая часть (11) не зависит от времени, то, дифференцируя её по ![]() , будем иметь, что
, будем иметь, что
![]() . (12)
. (12)
Значение ![]() в (12) нужно взять из
(1), когда
в (12) нужно взять из
(1), когда
![]() , (13)
, (13)
где ![]() , и суммирование по
, и суммирование по ![]() в (13) заменено
интегрированием:
в (13) заменено
интегрированием: ![]() .
.
Основной вклад в
интеграл (13) дают значения ![]() , когда
, когда ![]() ~ 1. Поэтому,
раскладывая подынтегральное выражение в ряд по значениям
~ 1. Поэтому,
раскладывая подынтегральное выражение в ряд по значениям ![]() и интегрируя по
и интегрируя по ![]() , найдем соотношение
, найдем соотношение
![]() , (14)
, (14)
где после замены ![]() функция
функция ![]() становится зависящей
от
становится зависящей
от ![]() и
и ![]() :
: ![]() .
.
Если волновой пакет
узкий (![]() ~
~ ![]() ;
; ![]() ), то
), то ![]() , и после подстановки (13) в (12) из (12) получим, что
, и после подстановки (13) в (12) из (12) получим, что
![]() . (15)
. (15)
Подставляя далее в
уравнение
![]()
значения ![]() из (10) и
из (10) и ![]() из (14), найдем
уравнение
из (14), найдем
уравнение
![]() . (16)
. (16)
Аналогично из (2)
получим уравнение для ![]() :
:
![]() (17)
(17)
Система уравнений (15) –
(17) является замкнутой и описывает пучковую неустойчивость в случае ![]() . При
. При ![]() ~ 1 нужно решать
совокупность интегро-дифференциальных уравнений, которые можно составить из (1)
– (3), (12), (13).
~ 1 нужно решать
совокупность интегро-дифференциальных уравнений, которые можно составить из (1)
– (3), (12), (13).
Исследуем задачу в
некоторых частных случаях. Пусть интенсивность колебаний зависит от ![]() следующим образом:
следующим образом:
![]() , (18)
, (18)
где ![]() только в области
только в области
![]() , (19)
, (19)
![]() а
а ![]() и
и ![]() не изменяются со
временем. Пусть также в (15) – (17) выполнены условия:
не изменяются со
временем. Пусть также в (15) – (17) выполнены условия: ![]() , и
, и
![]() . (20)
. (20)
Тогда получим, что,
![]() , (21)
, (21)
где
![]() .
.
Тогда для величин
![]() ;
; ![]() ;
;
![]()
получим следующее:
![]() ,
,
![]() , (22)
, (22)
![]() ,
,
![]() .
.
При ![]() из (22) найдем, что
из (22) найдем, что
![]() ,
,
![]() ,
,
![]() , (23)
, (23)
![]() .
.
Нетрудно убедиться, что
условие ![]() справедливо при
выполнении неравенства
справедливо при
выполнении неравенства
![]() . (24)
. (24)
Оно означает, что ![]() , и неравенства в (19) не очень отличаются от начальных (при
, и неравенства в (19) не очень отличаются от начальных (при ![]() ), поскольку справедливо следующее:
), поскольку справедливо следующее:
![]() , (
, (![]() ).
).
Подставляя (18) и (23) в
(14) можно найти, как изменяется со временем скорость ![]() каждой частицы:
каждой частицы:
![]() . (25)
. (25)
Соотношение (25)
показывает, что все частицы из области ![]() собираются в более
узкую область 1,6
собираются в более
узкую область 1,6 ![]() , т.е. происходит группировка электронов и появление выступа
на функции распределения частиц по скоростям
, т.е. происходит группировка электронов и появление выступа
на функции распределения частиц по скоростям ![]() , показанное на рис. 1а. При этом поверхность выступа
повторяет форму начальной поверхности из-за того, что была выбрана зависимость
, показанное на рис. 1а. При этом поверхность выступа
повторяет форму начальной поверхности из-за того, что была выбрана зависимость ![]() в виде (18). При
других зависимостях
в виде (18). При
других зависимостях ![]() форма
форма ![]() , естественно, другая. Можно утверждать также, что в случае
, естественно, другая. Можно утверждать также, что в случае ![]() ~ 1 формула (14)
сохранится (для этого необходимо только условие
~ 1 формула (14)
сохранится (для этого необходимо только условие ![]() ). Аналогично останутся пригодными и (15), (17), но (10) и
(16) – изменятся.
). Аналогично останутся пригодными и (15), (17), но (10) и
(16) – изменятся.
Можно утверждать также,
что рассмотренная картина справедлива не только в области ![]() , но и в соседних областях скоростей, где
, но и в соседних областях скоростей, где ![]() , хотя там инкременты меньше и все эффекты проявляются позже.
Значит можно ожидать, что весь интервал скоростей
, хотя там инкременты меньше и все эффекты проявляются позже.
Значит можно ожидать, что весь интервал скоростей ![]() покроется выступами
функции
покроется выступами
функции ![]() , т.е. возникнет картина, схематически показанная на рис. 1в.
, т.е. возникнет картина, схематически показанная на рис. 1в.
В случае горячих
электронных пучков в некоторых работах (см. [4] и др.) высказано допущение, что
они размываются по энергиям согласно уравнениям квазилинейной теории, но
строгих доказательств этому нет. В настоящей работе показано, что на первой
стадии размытия пучка, когда его функция распределения по скоростям ![]() трансформируется
только в области
трансформируется
только в области ![]() , квазилинейная теория не работает, потому что здесь
появляется система пиков функции распределения, которая не свойственна
квазилинейным уравнениям.
, квазилинейная теория не работает, потому что здесь
появляется система пиков функции распределения, которая не свойственна
квазилинейным уравнениям.
Проанализируем теперь
качественно решения уравнений (15) – (17) в случае достаточно большого размытия
частиц пучка по скоростям, когда ![]() существует в области
существует в области ![]() , где
, где ![]() . Предположим, что
. Предположим, что ![]() имеет вид, показанный
на рис. 2а,
имеет вид, показанный
на рис. 2а, ![]() , а интенсивность колебаний задана соотношением (см. рис.
2в):
, а интенсивность колебаний задана соотношением (см. рис.
2в):
![]() ,
, ![]() . (26)
. (26)
Тогда из (15) – (17)
получим, что
![]() ;
; ![]() ;
;
![]() ;
; ![]() (27)
(27)
где
![]() ;
; ![]() .
.
Из (27) следует, что
интервал ![]() возрастает со
временем, а высота
возрастает со
временем, а высота ![]() убывает, но
произведение
убывает, но
произведение ![]() остается постоянным,
т.е. площадь треугольника на рис. 2а не изменяется, т.к. нормирована на одну
частицу. При
остается постоянным,
т.е. площадь треугольника на рис. 2а не изменяется, т.к. нормирована на одну
частицу. При ![]() величина
величина ![]() сильно уменьшается,
так что интенсивность
сильно уменьшается,
так что интенсивность ![]() почти равномерно
распределена по интервалу скоростей
почти равномерно
распределена по интервалу скоростей ![]() .
.
Таким образом, решения
(27) системы (15) – (17) показывают «расползание» первоначально почти
моноэнергетического пучка электронов в пространстве скоростей, когда нижняя
граница ![]() движется к нулю, а
верхняя
движется к нулю, а
верхняя ![]() покоится.
покоится.
Запишем теперь очевидные
соотношения:
![]() ;
; ![]() .
.
Тогда с учетом (26)
получим вместо (15) уравнение
![]() ,
,
в котором ![]() по порядку величины
совпадает с коэффициентом диффузии
по порядку величины
совпадает с коэффициентом диффузии ![]() квазилинейной теории
[10]:
квазилинейной теории
[10]:
![]() .
.
Если учесть также
соотношение (10), совпадающее с квазилинейным, то можно заключить, что
уравнения квазилинейной теории качественно верно описывают воздействие волн на
пучок на более поздней стадии взаимодействия. Тем самым использование
квазилинейных уравнений для качественной оценки ситуации оправданно, хотя,
строго говоря, уравнение (10) и не является диффузионным.
Автор выражает благодарность академику К.Н.
Степанову за обсуждение работы.
Литература
1.
Сизоненко В.Л. Нормальное распределение частиц в турбулентной плазме // Матеріали III Міжнародної науково-практичної
конференції „Науковий потенціал світу – 2006”. – Дніпропетровськ: Наука і
освіта, 2006. – Т.9. – С.73-77.
2.
Сизоненко В.Л. // Вопросы Атомной Науки
и Техники. Украина. – 2008. – №4. – С.250-254.
3.
O`Neil T.M., Winfrey T.H., Malmberg T.H. // Phys. Fluids. 1971. V. 14.
P. 1204.
4.
Мациборко
Н.Г., Онищенко И.Н., Шапиро В.Д., Шевченко В.И. // Plasma. Phys. 1972. V. 14. P. 591.
5.
Мациборко
Н.Г., Онищенко И.Н., Файнберг Я.Б. и др. // ЖЭТФ. 1972. Т.63. С.874.
6.
Балакирев В., Андо Р., Камада К. и др. // Физика плазмы. 1997. Т.23. С.1042.
7.
Haeff A.V. // Phys. Rev. 1948. V.74. P.1532.
8.
Bohm D., Gross E.P.
. // Phys. Rev. 1949. V.75. P.1864.
9.
Ахиезер
А.И., Файнберг Я.Б. // ДАН СССР. 1949. Т.69. С.555.
10.
Веденов
А.А., Велихов Е.П., Сагдеев Р.З. // УФН. 1961. Т.73. С.701.
11.
Dupree T.P. // Phys. Fluids. 1966. V.9. P.1773.
12.
Orszag S.A., Kraichnan R.H. // Phys. Fluids. 1967. V.10. P.1720.
13.
Weinstock T. // Phys. Fluids. 1969. V.12.
P.1045.
14.
Weinstock T., Bezzerides // Phys. Fluids. 1973. V.16.
P.2287.
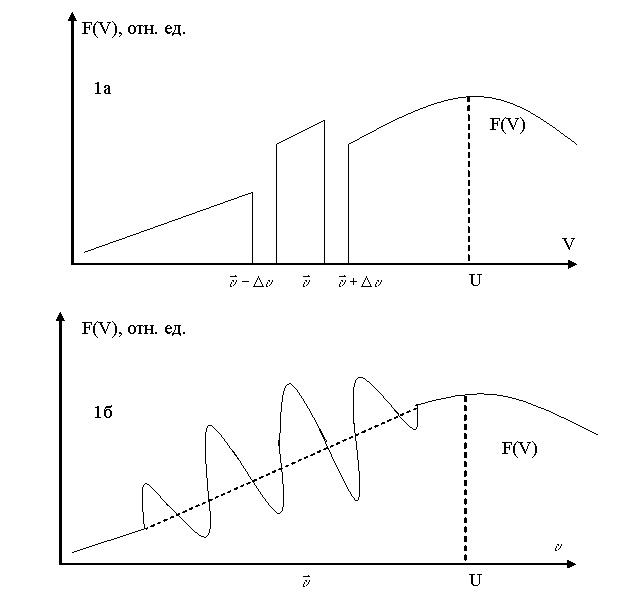
Рис. 1. статьи Сизоненко В.Л.
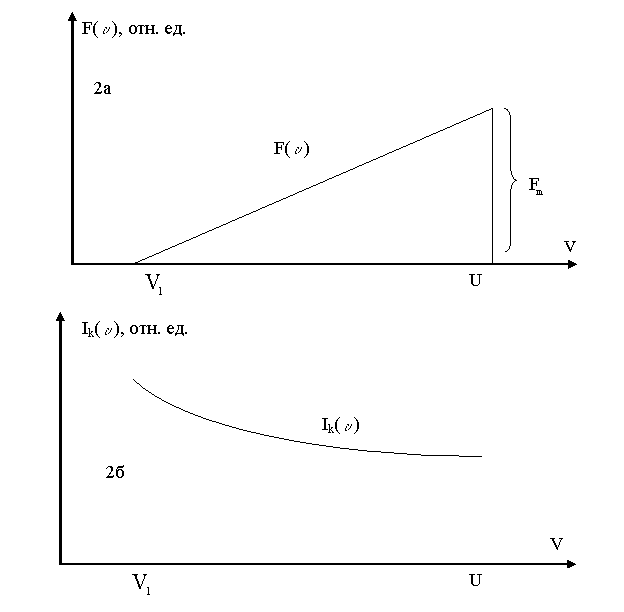
Рис. 2. статьи Сизоненко В.Л.
Подписи к рисункам
Рис. 1. Схематическая картина появления пиков на
функции распределения частиц пучка по скоростям.
Рис. 2. Схематические зависимости функции
распределения и интенсивности колебаний от ![]() .
.