ВІДНОВЛЕННЯ ЗОБРАЖЕНЬ З УРАХУВАННЯМ МЕТОДУ ДВООЗНАКОВОГО СТРУКТУРНОГО ДЕКОДУВАННЯ

Д.т.н., доц. Юдін О.К., Курінь К.О.

Національний авіаційний університет

ВІДНОВЛЕННЯ ЗОБРАЖЕНЬ З УРАХУВАННЯМ МЕТОДУ ДВООЗНАКОВОГО СТРУКТУРНОГО ДЕКОДУВАННЯ

Вступ

Стиснення даних є одним з найбільш актуальних напрямків сучасної теорії інформації, і цілком справедливо можна говорити про методи компресії як про один з найважливіших засобів|коштів| забезпечення оптимального і ефективного функціонування інформаційно-комунікаційних систем.

В [1] описаний принцип стиснення зображень, побудованого на базі методу двоознакового структурного кодування (ДСК). Структурно-логічна модель кодера ДСК включає наступні етапи:

1. Кольорове зображення переводиться у формат представлення для моделі RGB|. Піксели, кожної компоненти формують в блоки 8×8, що називаються сегментами зображення. Якщо число рядків або стовпців вихідного зображення не кратно 8, то верхній рядок і правий крайній стовпець, повторюють потрібну кількість разів.

2. До кожного сегменту зображення застосовують ДКП. В результаті трансформації матриці зображення на базі ДКП, отримують|одержуємо| блоки 8×8 частот одиниць даних.

Оскільки на даному етапі квантовані сегменти містять від’ємні значення, доцільно сформувати матриці знаків за правилом:

Тут - -й елемент матриці знаків, що надає інформацію про знак компоненти .

; , де ; - кількість рядків та стовбців растру зображення відповідно.

5. На цьому етапі застосовують базовий метод стиснення даних – кодування методом ДСК [2]. Завданням|задачею| даного етапу є|з'являється| формування кода-номера методом ДСК для двійкових послідовностей, які складають структуру зображення, згідно виявлених структурних надмірностей з урахуванням структурних ознак сегменту зображення. У результаті|унаслідок| здійснення даного кроку кодером формують масив значень кодів-номерів для|стискати| зображення, а також таблиці параметрів структурних ознак ДСК, що містять|утримують| значення векторів обмежень на позиції з|із| допустимою появою одиниць і числа серій одиниць в кожній з допустимих зон, які необхідні декодеру для подальшого однозначного декодування даних.

6. На цьому етапі застосовують кодування послідовностей кодів-номерів методом RLE| з метою збільшення ступеня|міри| стиснення початкового зображення.

Також на даному етапі за таким же принципом проводять|виробляє| кодування таблиці, що містить|утримує| значення числа серій одиниць в кожній з допустимих зон двійкових послідовностей, для яких сформовано код-номер та матриці знаків.

Сформований спосіб стиснення зображень дозволяє підвищити значення коефіцієнту стиснення в порівняні з відомими методами в 1,3-4,2 рази для більш широких класів джерел повідомлень

Постановка задачі

Мета|ціль| та завдання роботи: створення|створіння| математичної і структурно-логічної моделі декодера даних, стиснених з урахуванням методів (ДСК). При цьому до задач статті відноситься:

- визначення основних етапів процедури відновлення інформації декодером при формуванні декодованого потоку даних;

- оцінка розбіжності відновлених та вихідних зображень.

Опис основних принципів методу двоознакового структурного декодування

Двоознакове структурне кодування відноситься до методів стиснення без втрат якості інформації. Даний метод заснований на усуненні структурної надмірності шляхом виявлення закономірностей в двійкових послідовностях за деякою ознакою [2,3].

Суть даного методу полягає у формуванні кода-номера двійкової послідовності із заданим значенням структурної ознаки.

Згідно теореми про взаємооднозначність [2] двоознакового структурного представлення за заданим значенням кода-номера можна без внесення похибки відновити лише одну ДП . Система виразів, що забезпечує безпомилкове відновлення, описується теоремою про відновлення двоознакових структурних чисел (ДСЧ) [2]: ДП , що задовольняє системі обмежень (1) можна відновити без внесення похибки на основі значення кода-номера , враховуючи значення величин: довжини ДП , вектора обмежень на позиції одиниць та вектора обмежень на число серій одиниць в допустимих зонах – згідно системи виразів:

; (5)

, (6)

де – -й елемент -ї допустимої зони ДСЧ;

– рекуррентний параметр, що розраховується на основі системи виразів (4);

– початкове значення параметра , що дорівнює ;

– залишкове значення кода-номера , отримане для ДП , що складається з двійкових елементів:

. (7)

Значення величини :

(8)

Рекурентне співвідношення для визначення величини на -ому кроці обробки через значення залишкового кода-номера на -ому кроці обробки має вигляд:

; ; (8)

;

, – початкові значення залишкових кодів-номерів відповідно для -ї та -ї допустимих зон;

– кількість двоознакових ДП , у яких -й елемент дорівнює нулю, тобто ;

– кількість ДП, отриманих для -ї допустимої зони за кількістю серій одиниць для вектора :

;

– кількість комбінацій довжиною з числом серій одиниць вектора , що передують -й зоні оброблюваної послідовності.

Структурна схема декодера зображень на базі методу двоознакового структурного кодування

Розглянемо докладніше ітерації процедури відновлення.

Перша ітерація. Згідно процедури кодування, описаної в [1], на вхід декодера подаються дані: значення кодів-номерів ДСК, значення числа серій одиниць в кожній з допустимих зон ДП, для яких сформовано код-номер, матриці знаків - всі закодовані згідно методу RLE.

Тому на першому етапі процедури відновлення відбувається декодування RLE (Рис. 1).

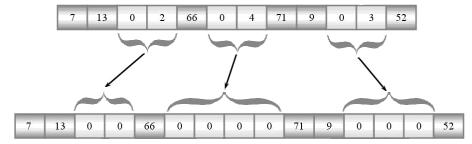
Рис. 1. Графічна модель алгоритму декодування RLE

Принцип декодування RLE полягає в наступному:|порядкового| якщо декодер отримує нуль (прапор), то це означає, що має бути відновлена послідовність нульових елементів, довжина відновлюваної послідовності визначається числом, що слідує за прапором, далі деко дер переходить до елемента, що слідує за значенням довжини послідовності нулів. Якщо на вхід декодера подається ненульовий елемент, то він записується у відновлену послідовність без змін і відбувається перехід до наступного елемента.

Також на даному етапі за таким же принципом проводиться|виробляє| відновлення таблиці, що містить|утримує| значення числа серій одиниць в кожній з допустимих зон ДП, для яких сформовано код-номер, та матриці знаків.

Друга ітерація. На даному етапі застосовується базовий метод декодування – ДСК. Завданням даного етапу є відновлення певної ДП у структурі зображення згідно кода-номера та відповідних структурних ознак. Суть даної процедури детально розглядається|розглядує| в [2]. Уточнимо, які саме складові структури |вихідних| зображення будуть відновлені (рис. 2).

Квантоване|вихідне| зображення розбивається на одиниці даних у вигляді сегментів розмірністю 8×8. Кожне з числових значень представляється у вигляді 8-бітового двійкового числа (тобто|цебто| кожним сегментом є паралелепіпед довжина якого складає 8 біт, а ширина і висота дорівнюють розмірності сегменту 8×8). Кожен сегмент складається з восьми шарів. До складу кожного шару входить по 8 стовпців розмірністю в 8 біт. На рис. 2 зображено описаний принцип просторової структуризації на прикладі Сегменту_1,8 із наведенням змісту кожного із шарів.

При кодуванні ДСК код-номер формувався для кожного стовпця кожного шару сегментів зображення [1]. Отже на цьому етапі декодування з кожного кода-номера буде відновлений один з восьми стовпців кожного з восьми шарів сегменту зображення. 64 коди-номери, що складають блок 8×8 у матриці кодів-номерів, визначатимуть відповідний сегмент квантованого зображення.

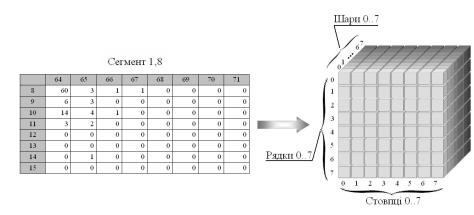
Рис. 4. Графічна модель структуризації зображень з урахуванням методу ДСК

Третя ітерація. На даному етапі відновлюються від’ємні значення компонент квантованих сегментів. Відновлення відбувається згідно вмісту матриць знаків за правилом:

Тут - -й матриці знаків, що надає інформацію про знак компоненти , - значення компоненти до відновлення інформації про її знак.

; , де ; - кількість рядків та стовбців растру зображення відповідно.

Кожен з 64 елементів у сегментах квантованого зображення множиться на число – коефіцієнт квантування і округляється до цілої частини|частки|.

Четверта ітерація. Далі до кожного трансформованого сегменту зображення застосуємо обернене ДКП [4]. Оскільки піксели корельовано по двом напрямкам, при відновлені використовується двовимірне обернене ДКП, що задається формулою:

де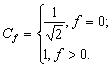

Тут р_ху - числові значення пікселів зображення, що містяться в сегментах розмірністю n×n, числові значення осередків трансформант розмірністю n×n (в даному випадку n=8). Значення i та j змінюються в межах від 0 до n-1.

П’ята ітерація. На останньому етапі процедури відновлення відкидаються продубльовані необхідну кількість разів до кратності з вісімкою верхній рядок та крайній правий стовпець. Блок-структурна модель, що описує основні етапи визначеного процесу відновлення даних, стиснених з урахуванням методу структурного двоознакового кодування двійкових послідовностей, представлена|змальовувати| на рис. 3.

Рис. 3. Блок-структурна схема реалізації процедури відновлення даних, стиснених|стиснення| з урахуванням методу ДСК

Для оцінки якості відновлених зображень використовується значення пікового відношення|ставлення| сигнал/шум [4]:

де - кількість двійкових розрядів, що відводиться|відводить| на представлення одного елементу вихідного зображення;

, - відповідно кількість рядків і стовпців в зображенні.

, - значення -го елемента відповідно для вихідного і відновленого зображень.

Згідно розрахунків, проведених після реалізації процедури кодування-декодування у програмному середовищі, були отримані значення пікового відношення сигнал/шум для різних класів тестових зображень: 53 дБ для дискретнотонових (штучних) зображень, 60 дБ для неперервнотонових (природних) зображень. Разом з тим в [1] було розраховано коефіцієнт стиснення для відповідних тестових зображень: 4,79 для для штучних зображень, 5,62 для природних зображень. На підставі отриманих даних були побудовані діаграми (рис. 7), які описують значення коефіцієнта стиснення для різних методів компресії при вказаних значеннях пікового відношення сигнал/шум (порядка 60 Дб).

Згідно наведених діаграм досягається виграш в стисненні:

- в 2,76 разів в порівнянні з методами JPEG-LS та JPEG, та в 2,2 рази в порівнянні з методом JPEG-2000 для природних зображень;

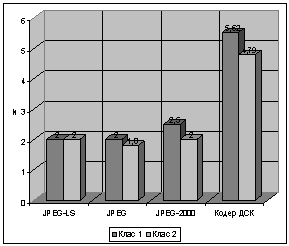
Рис. 7. Діаграми залежності величини при обробці різних видів зображень: 1 клас – реалістичні контрастні, 2 клас – штучні

- в 2,35 рази в порівнянні з методами JPEG-LS та JPEG-2000, та в 2,6 разів в порівнянні з методом JPEG-2000 для штучних зображень.

Висновки

Розроблено|створіння| математичну і структурну модель процедури декодування зображень, стиснених за допомогою методу, що враховує двоознакове структурне кодування двійкових послідовностей в структурі зображення. Визначено основні етапи процедури обробки інформації декодером. Розроблена процедура відновлення базується на виконанні наступних функцій:

1. Відновлення квантованих трансформант дискретного косинусного перетворення за методом двоознакового структурного кодування. Вміст відновлених трансформант не зазнає жодних спотворень, оскільки|тому що| декодер ДСК абсолютно однозначно відновлює початкові двійкові послідовності.

2. Виконання процедури деквантування.

3. Виконання оберненого дискретного косинусного перетворення.

4. Отримання колірних компонент вихідного зображення.

Проведено оцінку розходження відновлених та вихідних зображень. Для розробленого методу значення цієї величини склало близько 60 Дб для широкого класу зображень. Вдалося досягти збільшення ступеня стиснення у порівнянні з існуючими методами в середньому в 2,5 рази для штучних та природних зображень.

Література

1. Юдін О.К. Структурно-логічна модель кодера стиску інформаційного потоку даних / Юдін О.К., Чеботаренко Ю.Б., Курінь К.О. // Вісник Інженерної академії України. – К., 2010. – 4 вид. – c. 151-157.

2. Юдін О.К. Кодування в інформаційно-комунікаційних мережах: – Монографія. - К.: НАУ, 2007.-308с

3. Yudin O.K. The parallel bi-indication encoding end renewal of data in binary polyadic space// Вісник НАУ. – 2006. – №4.– С. 3-7