Балюба И.Г., д.т.н.; Горягин Б.Ф., к.т.н; Малютина Т.П., к.т.н.

Донбасская национальная академия строительства и архитектуры

Обобщенные тригонометрические функции

и их применение

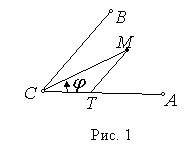В прямоугольной декартовой системе координат заданы три точки , которые определяют общую плоскую декартовую систему координат (рис.1). При точечном описании геометрических объектов плоскости в пространственной системе с угловым параметром полезно использовать отношение сторон треугольника , где параллельно . Естественно эти отношения назвать тригонометрическими функциями: , .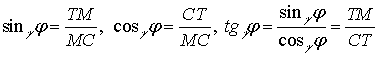

Когда , то обобщенные тригонометрические функции превращаются в обычные: .

Эллипс заданный сопряженными полуосями

В качестве эффективности предложенного обобщения рассмотрим пример точечного уравнения окружности в прямоугольном симплексе :

.

При параллельном проецировании прямой угол исказится до , а отрезки и прямоугольного равнобедренного треугольника , в общем случае не будут равны. Уравнение окружности станет уравнением эллипса с сопряженными полуосями и : .

Чтобы последнее уравнение имело практический смысл, выразим обобщенные тригонометрические функции через обычные тригонометрические функции. Из треугольника (рис.1), по теореме синусов имеем:

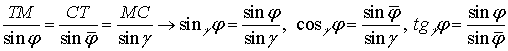, где .

Окончательно точечное уравнение эллипса заданного сопряженными полуосями принимает вид: .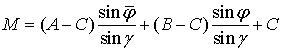

Полярная параметризация плоскости

В естественной параметризации плоскости имеем точечное уравнение : ,

где .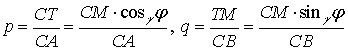

Введем обозначения . После подстановки получим полярную параметризацию плоскости :

.

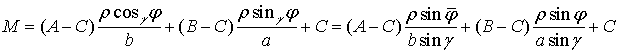Принимая получим точечное уравнение окружности радиусом с центром в точке в плоскости общего положения :

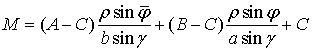, где .

Полярная параметризация удобна для точечного задания спиралей , так например, при получим уравнение двух ветвей спирали Архимеда ():

.

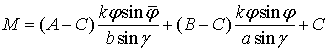Биугловая параметризация плоскости

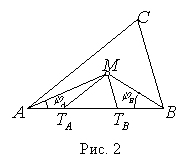
Определим точку плоскости с параметрами (рис.2):

.

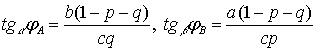Для определения естественных параметров получим систему уравнений:

.

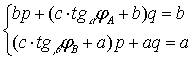Из этой системы определяем:

,

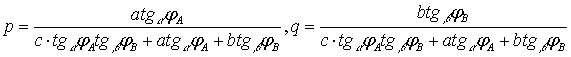где .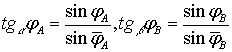

После подстановки получим параметризацию плоскости двумя углами и :

.

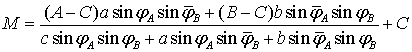В равностороннем симплексе :

.

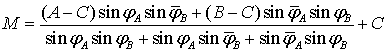Использовать биугловую параметризацию плоскости удобно при конструировании кривых с осями симметрии. В частности при будем иметь окружность, проходящую через вершины симплекса.

Тогда принимаем :

,

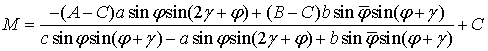где , .

Литература

1. Балюба И.Г., Полищук В.И., Горягин Б.Ф., Малютина Т.П. Точечное исчисление - математический аппарат параллельных вычислений для решения задач математичеc-кого и компьютерного моделирования геометрических форм. Материалы Междуна-родной научной конференции «Моделирование – 2008», 14-16 мая 2008 р., г. Киев, Т.2. – С.286-290. Институт проблем моделирования в энергетике им. Г.Е. Пухова НАН Украины.

2. Погібєлєва Х.С., Малютіна Т.П. Формоутворення спіралей та їх аналітичне представ-лення. Графика XXI века. Тезисы докладов XIII Международной студенческой научно-технической конференции, 4 – 8 октября 2010 г., г. Севастополь.