И.А. Долгарев и А.И. Долгарев

КАППА-ФУНКЦИЯ ЕВКЛИДОВА ВЕКТОРА.

ГАЛИЛЕЕВЫ НАТУРАЛЬНЫЕ УРАВНЕНИЯ ЕВКЛИДОВОЙ ЛИНИИ

(обзор теории кривых)

 

Работа отражает результаты из теории евклидовых кривых, полученные в последнее время. Регулярность кривой влечет неоднородность пространства, что согласуется с вложением евклидова пространства в пространство-время. Каппа-функция евклидова вектора выявляет полезные свойства кривых. Привлечение галилеевых понятий вносит свежую струю в исследования и приложения, приводит к галилеевым натуральным уравнениям кривой, сближая евклидову и галилееву геометрии. Отмечена одна грань естественной параметризации линии. Использована связь с механикой.

 

1. Основные понятия и свойства

            Обзор содержит и известные свойства кривых, необходимые в изложении. Рассматривается 3-мерное евклидово пространство . С векторной функцией

,

задающей евклидову кривую, связана скалярная функция , выделяется функция  постоянного модуля  = , . Функции  считаются непрерывными и дифференцируемыми, используется  = . Вектор производной вектора постоянной длины перпендикулярен исходному вектору . Со всяким вектором  связана скалярная функция, получающаяся при дифференцировании единичного вектора, так называемая каппа-функция вектора .

 

1.1. Каппа-функция евклидова вектора

            Введена каппа-функция в [1, c. 59 – 61]. Пусть  дифференцируемый вектор,  единичный вектор направления .

1.      ЛЕММА. [2, лемма 1]  Производная единичного вектора есть

 = .                                               (1)

            2. ЛЕММА. [2, лемма 2] Производная (1) записывается в виде:

 = , .                                                (2)

            ОПРЕДЕЛЕНИЕ 1. [2, определение 1] Каппа-функцией (функцией) вектора  называется модуль вектора , т.е.

= .

В случае 2-мерного вектора :

.

Выполняются соотношения

,  , .                                             (3)

            Леммы 1 и 2 и определение 1 подчеркивают, что  произвольный 3-мерный евк-

лидов вектор, не связанный ни с каким геометрическим образом. Если вектор описывает линию, то используется обозначение . Имеем по (1) для :

3.      ТЕОРЕМА. [2, свойство 13] Модуль производной (1) равен

 =  = .                                     (4)

Вектор в числителе равенства (4)

рассматривается в [3, с. 32; 4, с. 162; 5, с. 98 – 102]. Появляется вектор в результате вычисления двойного векторного произведения . Но нигде не упоминается и не используется функция вектора .

            4. ЛЕММА. [2, лемма 12]  функция вектора  вычисляется и по формуле

 =  .                                                          (5)

            Получается равенство в результате возведения функции вектора  в квадрат. В частности, по (4):

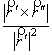 = .                                                        (6)

Равенство дополняет теорему 3.

Для векторной функции вида  =  выполняется

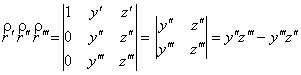,                          (7)

см. лемму 16 в [2].

5.                  СВОЙСТВО. Ненулевой дифференцируемый вектор  и операция дифференцирования единичного вектора задают в 3-мерном евклидовом пространстве 2-мерное направление , см. (1),  и поворот четвертого порядка вокруг оси, определяемой вектором ; считается, что векторы  приложены в некоторой фиксированной точке , .

            В пространстве  определяется естественным образом репер  = , где ; , вектор   отыскивается в дифференцировании   = , ; , или еще . В дифференцировании вектора  получается вектор , в дифференцировании вектора  получается вектор , затем  и наконец . Полезен репер в случае , это сопровождающий репер кривой .

 

1.2. Кривая в естественной параметризации

            ОПРЕДЕЛЕНИЕ 2. Отображение интервала  числовой прямой  в евклидово пространство  называется кривой или линией евклидова пространства,

.

            Описывается кривая векторной функцией

 = , .                                   (8)

Кривая  есть множество точек

            ОПРЕДЕЛЕНИЕ 3. Кривая  называется регулярной класса , если функция  не менее трех раз дифференцируема и .

Точки регулярной кривой называются обыкновенными. Точки кривой, в которых происходит нарушение регулярности, называются особыми. Далее рассматриваются регулярные кривые в окрестности обыкновенной точки. Вектор  называется вектором касательной кривой ,пусть  обыкновенная точка; касательная есть прямая .  Плоскость, перпендикулярная касательной в точке , называется нормальной к кривой в точке .

            Длина дуги линии  от точки  вычисляется по формуле

.

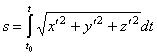Имеется функция , существует обратная к ней функция  . В задании (8) заменим параметр:

.

Полученная параметризация линии (8) называется естественной, параметризации (8) произвольна. Производные функции  обозначаются , . Справедлива

            6. ЛЕММА. .

            С кривой   связан сопровождающий репер  = , где  лежит на кривой, , , . Единичные векторы репера:  вектор касательной,  вектор главной нормали,  вектор бинормали. Координатные оси:  касательная кривой,  главная нормаль кривой,  бинормаль кривой. Координатные плоскости:  соприкасающаяся плоскость,  спрямляющая плоскость,  нормальная плоскость.

            7. ТЕОРЕМА. Положение касательной к кривой не зависит от ее параметризации.  Положение соприкасающейся плоскости кривой не зависит от параметризации кривой; =.

            8. ТЕОРЕМА. Векторы сопровождающего репера кривой в произвольной параметризации таковы: .

            Таким образом, сопровождающий репер кривой не связан с естественной параметризацией кривой, см. лемму 6 и [6].

 

1.3. Кривизна и кручение кривой

            ОПРЕДЕЛЕНИЕ 4. Кривизной евклидовой кривой  называется величина

, .

            9. ТЕОРЕМА. Производные единичных векторов сопровождающего репера равны

.                                         (9)

            Вектор  называется еще вектором кривизны линии . Формулы (8) называются формулами Френе.

            ОПРЕДЕЛЕНИЕ 5. Введенная во второй формуле Френе величина  называется кручением линии .

            10. ТЕОРЕМА. Производные векторов сопровождающего репера кривой выра-жаются только через векторы сопровождающего репера и кривизну и кручение кривой.

            11. ТЕОРЕМА.  если и только если кривая плоская.  если и только если линия является прямой; кривизна прямой равна нулю.

            Вычислительные формулы в естественной параметризации:

=,  =;

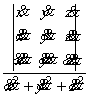в произвольной параметризации формулы для вычисления кривизны и кручения есть:

,  .                                             (10)

Для плоской кривой

,   .

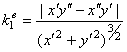            Если задана евклидова регулярная линия векторной функцией , то определены две скалярные функции кривизны  и кручения  линии.

            По лемме 4 и теореме 3 выполняется

            12. ТЕОРЕМА [2, свойство 6, теорема 13]. Евклидова кривизна кривой выражается через функцию производной: .

 

1.4. Кривая в выделенной параметризации

            В параметризации (8) ввиду регулярности кривой каждая из покомпонентных функций  обратима. Пусть . Регулярная кривая записывается в параметризации

= .                                                  (11)

Эта параметризация кривой называется выделенной. Параметризация вида (8), в том числе и естественная, описывает регулярную кривую симметричной функцией, параметризация (11) несимметричная, в ней выделена одна из компонент. Выделена может быть и другая компонента. Кривая (11)  задается как пересечение двух цилиндрических поверхностей

                                                           (12)

(11) и (12)  являются явным заданием кривой, т.е. заданием кривой явными функциями.

            Параметризация (11) не может быть естественной, так как  , , поэтому .

            По (6) и второй формуле в (10) имеем в выделенной параметризации

 = .                                                    (13)

            13. ТЕОРЕМА. В выделенной параметризации

.                                                    (14)

Формула следует из (10), (5), (13).

 

1.5.Соприкасающиеся окружность и парабола

Пусть  не является прямой линией, в этом случае . На нормали  к кривой  в точке  существует точка  в сторону вогнутости линии такая, что . Величина  называется радиусом кривизны линии  в точке , точка  называется центром кривизны линии  в точке , окружность с центром  и радиусом  , называется соприкасающейся окружностью линии  в точке .

            В дифференциальной окрестности второго порядка точки  линии  содержатся соприкасающаяся окружность и соприкасающаяся парабола, [7, с. 74 – 75].

 

1.6. Замечательные евклидовы линии

            В естественной параметризации прямая описывается функцией

 = , ; .

, ; кривизна и кручение прямой равны нулю: , . Линия нулевой кривизны является прямой, что получается в результате интегрирования системы уравнений .

            Кривизна окружности  радиуса  равна .

            14. ЛЕММА [8, лемма 1]. В естественной параметризации окружность кривизны  описывается функцией

 = ,  .

            В общем случае выполняется

            15. ТЕОРЕМА [8, теорема 3] Если задана дифференцируемая функция , то в естественной параметризации кривая с кривизной  имеет вид , где

, , .              (15)                                            

Начальные условия вида , определяют единственную линию, проходящую через данную точку  в направлении данного единичного вектора .

            Кривизна и кручение винтовой линии радиуса  с шагом  постоянны и равны соответственно

,  ;

У винтовой линии модуль вектора касательной есть .

16.             ТЕОРЕМА [8, теорема 4]. В естественной параметризации винтовая линия кривизны  и кручения  описывается векторной функцией

 = .                 (16)

17.              ТЕОРЕМА [8, теорема 5]. Если заданы кривизна  и кручение равно  винтовой линии , то функции  задания = , ,  винтовой линии  являются решениями системы обыкновенных дифференциальных уравнений

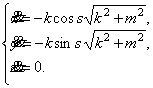
Начальные условия вида

;  ,  ;

,;

 , 

определяют единственную линию, проходящую через точку  в направлении вектора .

            В номере цитируемой теоремы в [8]  допущена опечатка, ее номер есть 5, а не 4. В общем случае выполняется

18. ТЕОРЕМА [8, теорема 6]. Если заданы функции , , то пространственная линия =  определяется в результате решения системы обыкновенных дифференциальных уравнений

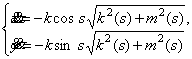
и функцией .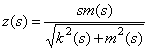

 

1.7. Натуральные уравнения регулярной евклидовой кривой

            Кривизна и кручение евклидовой регулярной кривой не зависят от параметризации кривой [4, с. 179 – 181], и не зависят от выбора репера, в котором кривая рассматривается. Вместе с тем, в теории евклидовых кривых доказана

            19. ОСНОВНАЯ ТЕОРЕМА ТЕОРИИ КРИВЫХ. Если на некотором интервале  заданы дифференцируемые функции

,  ,                                         (17)

то кривая  на интервале  определяется однозначно с точностью до положения в пространстве. [4, с. 137 – 144, 196 – 208].

            Функции (17) называются натуральными уравнениями кривой. В малой окрестности обыкновенной точки евклидова кривая с кривизной  описывается функциями (15), см. теорему 15. В малой окрестности обыкновенной точки  евклидова кривая с кривизной  и кручением  описывается функцией (16) при , ,  , , .

 

1.8. Строение регулярной евклидовой кривой

            20. ТЕОРЕМА. [4, с. 185 – 191]. В окрестности обыкновенной точки регулярная евклидова кривая является либо отрезком прямой (, ), либо дугой окружности или параболы (,), либо дугой винтовой линии (,).

 

2. Элементы галилеевой теории кривых

2.1. Пространство-время Галилея

            Рассматривается событие , состоящее в том, что в момент времени  точка имеет координаты . Множество всех событий есть мир и совпадает с многообразием . События рассматриваются в двух качествах – как векторы и как точки. Пусть  и . Операции над событиями как векторами задаются равенствами

= += , , .     (18)

События составляют линейное пространство  над . Пусть =  и =  точки, множество точек обозначается . Задано отображение пар точек в линейное пространство . Паре событий  соответствует вектор . Считается, что указанное отображение удовлетворяет аксиомам Г. Вейля аффинного пространства, [9, с. 27 – 28]. Множество  является аффинным пространством. Всякая точка  и всякий ненулевой вектор  определяют единственную прямую  в , описываемую векторной функцией

=, .                                         (19)

Множество точек, описываемое функцией

=, ,                                             (20)

называется линией аффинного пространства.

            Для векторов из  определено  галилеево скалярное произведение векторов

Галилеевой нормой вектора  называется ,

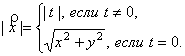                                                (21)

Галилеево расстояние между точками  и , согласно (21), равно

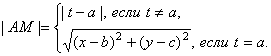
Первые компоненты векторов и точек называются временными, вторые и третьи компоненты векторов и точек называются пространственными. Линейное пространство  при этом становится галилеевым векторным пространством , аффинное пространство превращается в пространство-время Галилея . Подробнее о геометрии пространства-времени  см. [1, с. 46 – 101]. Аффинные прямые (19)  являются прямыми в , линии (20) являются линиями в . Производные галилеевых функций (20) отыскиваются покомпонентно:

.

Векторы вида , согласно операциям (18),  составляют в  2-мерное евклидово пространство , т.е. это евклидовы векторы в пространстве Галилея. Пространство-время Галилея  содержит евклидовы плоскости , где  базис линейного пространства , прямая  есть ось времени в . Через всякую точку пространства  проходит единственная евклидова плоскость и  является прямой суммой оси времени и евклидовой плоскости .

 

 

2.2. Кривая пространства-времени Галилея

Линию (20) считаем регулярной класса , если функция не менее трех раз

дифференцируема, ; при этом и компонента  дифференцируема и отлична от нуля. Из условия регулярности линии следует обратимость функции , существует функция . Линия (20) записывается в параметризации

 = .                                                      (22)

Это естественная параметризация галилдеевой кривой,

,

по (21),

.

            Кривизной галилеевой кривой (22) называется величина

,                                                     (23)

как и в евклидовой геометрии, кривизна галилеевой кривой есть модуль вектора производной 2-го порядка линии (22) в естественной параметризации. Кручением галилеевой линии (22) называется функция евклидова вектора , см. п. 1.1,

,                                                 (24)

т.е. кручение галилеевой кривой определяется в дифференцировании вектора кривизны .

            По вычислительным формулам кривизны (23) и кручения (24) составлена система обыкновенных дифференциальных уравнений

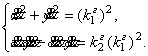                                                 (25)

            21. ТЕОРЕМА. [10, п. 2.3]  Если заданы дифференцируемые функции

                                         (26)

на интервале , то решение  системы (25) определяет с точностью до положения кривую (22) пространства-времени Галлея, имеющую заданные кривизну и кручение.

            По виду первого уравнения системы (25) вводятся функции

;                       (27)

они удовлетворяют и второму уравнению системы (25). Функции  отыскиваются в результате двукратного интегрирования дифференциальных уравнений из (27). Начальные условия вида ,  выделяют единственную кривую пространства-времени , проходящую через данную точку  и имеющую касательную с данным вектором .

            Плоская кривая постоянной кривизны  отыскивается при решении обыкновенного дифференциального уравнения

и является параболой

;

пространственная кривая постоянной кривизны  и постоянного кручения  отыскивается в результате интегрирования системы обыкновенных дифференциальных уравнений (25) и является винтовой линией вида

 = ,

[1, с. 66 – 67]. Направляющей круглого цилиндра, на котором лежит винтовая линия, является окружностью евклидовой плоскости

 = ,

ее радиус и евклидова кривизна . Отсюда получается  зависимость  

, [1, с. 67].

22. ТЕОРЕМА. В окрестности обыкновенной точки линия пространства Галилея является либо отрезком прямой, либо дугой параболы, либо дугой винтовой линии.

Т.е. строение регулярной галилеевой кривой такое же, как и строение евклидовой регулярной кривой, теорема 20.

 

3. Галилеевы свойства евклидовой кривой.

Неоднородность евклидова пространства  

3.1. Свойства кривых, зависящих от выбора скалярного произведения векторов

Линии аффинного пространства описываются векторными функциями (8), важный частный случай – прямые. Вводя в аффинном пространстве  аффинного пространства  скалярное произведение векторов, получаем соответствющее пространство со скалярным произведением. Если выбрано собственно евклидово скалярное произведение векторов, то имеется собственно евклидово пространство , его свойства изучает евклидова геометрия. Если выбрано галилеево скалярное произведение векторов, то  превращается в пространство-время , его свойства изучает геометрия Галилея. Имеется много галилеевых пространств, [1], одно из них – коммутативное и линейное, названо пространством Галилея. Все объекты аффинного пространства, в частности кривые, обладают не только аффинными свойствами, но и евклидовыми свойствами, и галилеевыми свойствами, и другими; но выявляются метрические свойства геометрических объектов при наличии скалярного произведения векторов. О евклидовых и римановых свойствах геометрических объектов много сказано в [11], см. например, с. 177, 195, 199, 263 и т.д.. Имеется единая геометрия 3-мерного многообразия , [12]. Одна и та же линия обладает и аффинными, и евклидовыми, и галилеевыми свойствами. В частности, евклидова линия обладает галилеевыми свойствами.

 

3.2. Галилеевы кривизны евклидовой регулярной кривой

Галилеевы натуральные уравнения кривой

            Введены галилеевы кривизны евклидовой регулярной кривой в [13] и подробно исследованы в [2]. Рассматривается выделенная параметризация кривой, п. 1.4.

            ОПРЕДЕЛЕНИЕ 6. [2, определение 1] Галилеевой кривизной евклидовой кривой (11) =  в ее обыкновенной точке называется величина

= =  = ;                                    (28)

Это аналог определения (23) кривизны галилеевой кривой и определения 4 кривизны евклидовой кривой. Вектор  называется вектором галилеевой кривизны  евклидовой кривой, единичный вектор галилеевой кривизны есть

 =  = .                                   (29)

Находим согласно п. 1.1:

 = , =: ; . .  (30)

            ОПРЕДЕЛЕНИЕ 7. [2, определение 2] Галилеевым кручением евклидовой кривой (11) называется величина

 =  = .                                         (31)

Вектор  называется  вектором галилеева кручения евклидовой кривой, единичный вектор галилеева кручения есть .

Вектор  характеризует отклонение кривой  от соприкасающейся плоскости .

23. ТЕОРЕМА. [2, теорема 9] Евклидова линия (11) является плоской, если и только если  . Линия (11) является прямой, если и только если ; при этом и .

По вычислительным формулам (28) и (31) получается система обыкновенных дифференциальных уравнений

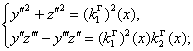                                           (32)

которая отличается от системы (25) только предназначением: (25) написана для кривой  пространства-времени Галилея , а (32) – для евклидовой кривой  в выделенной параметризации.

            24. ТЕОРЕМА. [2, теорема 3] Компоненты  кривой (11) в выделенной параметризации являются решением системы обыкновенных дифференциальных уравнений (32), где ,  заданные на интервале  функции класса  галилеевых кривизн. Единственная кривая (11)  определяется начальными условиями

, ,   .

            Компоненты  отыскиваются в решении уравнений

.

Галилеевыми натуральными уравнениями евклидовой кривой называются , . По галилеевым натуральным уравнениям евклидова кривая отыскивается значительно проще, чем по евклидовым натуральным уравнениям.

Следовательно, регулярная евклидова кривая в окрестности обыкновенной точки есть либо отрезок прямой, либо дуга параболы, либо дуга винтовой линии, это отмечено в теореме 20, п. 1.8.

 

3.3. Зависимости между евклидовыми и галилеевыми кривизнами

евклидовой кривой

Выше получены теорема 12 и формула (14):

,  .

Первая из них есть   = .

            На основе второй и независимо в [2] имеем

            25. ТЕОРЕМА. [2, теорема 18] Евклидовы и галилеевы кривизны евклидовой кривой связаны соотношением

.

 

3.4. Плоскость галилеевых кривизн. Неоднородность евклидова пространства

            ОПРЕДЕЛЕНИЕ 8. [2, п. 2.1] Плоскость  называется плоскостью галилеевых кривизн евклидовой линии (11). О векторах  см. (29) и (30) в п.3.2.

Плоскость  является соприкасающейся. Репер  называется галилеевым сопровождающим репером евклидовой кривой.

            26. ТЕОРЕМА. [2, теорема 10] Не существует плоскости галилеевых кривизн для плоской евклидовой линии.

            27. ТЕОРЕМА. [2, теорема 11]  Плоскость галилеевых кривизн  евклидовой линии имеет в евклидовом пространстве неизменное направление, она движется параллельно сама себе при движении точки  по линии.

            При движении точки  по линии  плоскость галилеевых кривизн  не может

двигаться, скользя сама по себе, так как в этом случае она перестает существовать, теорема 26. Плоскость  существует, если она занимает различные положения в евклидовом пространстве.

            28. ТЕОРЕМА. [2, теорема 21] Перемещение плоскости галилеевых кривизн  евклидовой кривой происходит под воздействием вектора

,

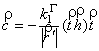который является ненулевой проекцией вектора  на вектор .

            Имеется составляющая  вектора  в (4), параллельная вектору . В механике вектор скорости вращения плоскости   определяется ненулевым вектором , коллинеарным вектору .

            29. ТЕОРЕМА. [2, теорема 22] Скорость вращения плоскости галилеевых кривизн  равна = .

            Пусть кривая  задана в репере . С каждой пространственной кривой  связан свой подвижный репер , где  плоскость галилеевых кривизн линии . Репер  вместе с точкой  по кривой  движется так, что плоскость  движется параллельно сама себе. Можно рассматривать выделенную параметризацию  =  той же кривой . В этом случае имеем подвижный репер . Репер  вместе с точкой  движется так, что плоскость  движется параллельно сама себе. Значит, при движении точки  по заданной кривой,  совпадающей с , репер  движется так, что координатные оси не изменяют направлений, а тогда и всякий вектор  в рассматриваемом движении не изменяет своего направления. Откуда следует, что  является прямой линией, что противоречит выбору линии , имеющей ненулевое кручение. Тем самым, выбирая выделенную параметризацию кривой , нужно выбрать и инвариантный вектор; выбран вектор . Рассматривая все кривые евклидова пространства в фиксированном репере , мы вынуждены при их изучении фиксировать направление  в пространстве, т.е. мы вынуждены согласиться с тем, что евклидово пространство , содержащее регулярные кривые, является неоднородным.

            При изучении формул Лоренца 4-мерного пространства-времени специальной теории относительности (СТО) выясняется, [11, с. 198 – 201], что пространственная составляющая этого пространства неоднородна, в пространстве выделяется 2-мерное инвариантное евклидово направление, [14]. Этот факт, согласно [15], верен и для пространственной составляющей пространства-времени Галилея , являющееся предельным случаем пространства-времени СТО. В связи с этим выполняется

30. ТЕОРЕМА. Имея только неоднородное евклидово пространство, невозможно получить пространство СТО и пространство Галилея.

Считается, что последнее есть прямая сумма оси времени и евклидова пространства, [16, с. 11 – 14]. В соответствии с Эрлангенской программой Ф. Клейна, существует не менее двух видов евклидовых геометрий:  элементарная евклидова геометрия – однородная геометрия и дифференциальная евклидова геометрия – изучающая регулярные кривые, см. [17].

            31. ТЕОРЕМА. [17, п. 4] Евклидово пространство, содержащее регулярные кривые, является неоднородным.

 

3.5. Определяемость евклидовой кривой вектором галилеевой кривизны

            Известна задача И. Ньютона о задании траектории движения материальной точки вектором ускорения движения, [16, c. 17 – 16]. Анализируя ситуацию, в [16, с. 26, аннотация к § 5] В.И. Арнольд приходит к выводу: “Анализ общей потенциальной системы с двумя степенями свободы выходит за рамки возможностей современной науки.“ Задача И. Ньютона решена средствами геометрии Галилея, [18, 19]. Используя решение системы обыкновенных дифференциальных уравнений (25), сводящееся к решению уравнений из (27). т.е. траектория движения определяется с точностью до положения в пространстве вектором ускорения движения, при этом решение задачи тривиально. Вектор ускорения движения по траектории   есть вектор ее галилеевой кривизны.

           32. ТЕОРЕМА. [20,  теорема 5]  Регулярная евклидова кривая однозначно, с точностью до положения в пространстве, определяется вектором галилеевой кривизны.

            Итак, для получения евклидовой кривой (11) можно задать две функции  и  галилеевых кривизн линии (17) или две функции  компонент вектора галилеевой кривизны этой кривой. Для регулярной евклидовой кривой (11) вектор галилеевой кривизны есть

.

Если задан вектор , то вектор  отыскивается в результате решения дифференциальных уравнений

.                                                     (33)

 

4. Дифференциальные уравнения кривых

4.1. Определяемость кривой дифференциальными уравнениями.

            На основании теоремы 19, в окрестности обыкновенной точки плоская регулярная евклидова кривая в естественной параметризации определяется как решение системы обыкновенных дифференциальных уравнений (15) по заданной функции кривизны , теорема 14. В окрестности обыкновенной точки  кривая есть дуга окружности радиуса . Пространственная регулярная евклидова кривая в окркстности обыкновенной точки  определяется в естественной параметризации как решение системы обыкновенных дифференциальных уравнений

  ,

при заданных значениях кривизны и кручения , . Кривая представляется дугой винтовой линии, теорема 16. Соответствующая система дифференциальных уравнений определяет кривую функциями , , теорема 17.

            Галилеевы натуральные уравнения ,  евклидовой кривой  определяют регулярную евклидову кривую как решение системы обыкновенных дифференциальных уравнений (32):

,  ,

теорема 23. дальнейшие исследования показали, см. п. 3.5, что регулярная евклидова кривая  определяется вектором кривизны и системой дифференциальных уравнений

.

 

4.2. Различные параметризации кривой

            При получении некоторой известной линии по ее натуральным уравнениям, линия может предстать в другой параметризации. Например, рассмотрим евклидову кривую

 = ,

перейдем к выделенной параметризации, заменив

 = .

Находим по формулам (28) и (31) галилеевы кривизны рассматриваемой кривой

 = ,  = ;

имеем систему обыкновенных дифференциальных уравнений вида (32). Находим: . По виду первого уравнения системы вводим обозначения

,  .

Получаем решение системы уравнений при подходящих начальных условиях с учетом произведенной замены

Выполняется равенство , как и для первоначально заданной функции, следовательно, найдена в другой параметризации та же кривая, что и первоначальном задании.

 

4.3. Одна кривая в различных геометрия

            В п. 3.1. отмечается существование единой геометрии многообразия , [12]. Кривые этой геометрии обладают аффинными, евклидовыми, галилеевыми свойствами (подразумевается коммутативная геометрия, рассматриваемая в аксиоматике Г.Вейля на линейном пространстве  над ). Однако, на многообразии  определены некоммутативные алгебраические структуры – одули Ли, [1, c.106 – 109]. Последние обобщают линейное пространство. Геометрии пространств с одулями Ли обобщают аффинную геометрию, [1, с. 128 – 129], всякая из одулярных геометрий есть часть геометрии многообразия  и является некоммутативной. Кривая  =  геометрии многообразия  обладает и одулярными свойствами, которые выявляются заданием соответствующих операций на тройках из , например, операция

определяет на  растран, [1, c. 107. В [1, c. 136 – 164] изложена дифференциальная геометрия пространства с растраном. Дифференцирование одулярных функций своеобразно и зависит от операций на одуле Ли. Например, растранная функция  =  дифференцируется по правилу

 = ,

[1, c. 126]. Кривизна  растранной кривой  =  вычисляется по формуле

 = .

Кручение  кривой  вычисляется как каппа-функция евклидова вектора  и равно

= .

Кривая  однозначно определяется своими натуральными уравнениями =, =  в результате решения системы обыкновенных дифференциальных уравнений

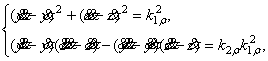
см. [10]. Для сравнения см. систему обыкновенных дифференциальных уравнений (32). По аналогии с теоремой 32 об определяемости евклидовой кривой вектором галилеевой кривизны выполняется

            33. ТЕОРЕМА. Евклидова регулярная кривая =  (т.е. кривая многообразия ) определяется вектором кривизны = растранной кривой  в результате решения системы обыкновенных дифференциальных уравнений

.                                                 (34)

            В данном случае компоненты одной и той же кривой  многообразия  являются решением систем уравнений вида (33) и (34); правые части уравнений различны.

Уравнения (33) проще. Для кривых других одулярных пространств, являющихся частями геометрии многообразия , получены другие системы обыкновенных дифференциальных уравнений, [10].

 

Литература.

  1. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005. – 306 с.
  2. Долгарев А.И.Галилеевы и евклидовы кривизны евклидовых кривых. - Materiali IX   

      mezinarodni vedecko-hraktika conference «Aktualni vymozenosti vediy – 2013» - Dil 17

            Matematika. Fizika. Moderni informacni technologie. Vystavba a archtektura: Praga.

 Publiching House “Education and Skience”. s.r.o. 2013 –  С. 7 – 17.

3.      Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия. – М.: Изд-во МГУ, 1990. –

      384с.

4        Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.

5        Выгодский М.Я. Дифференциальная геометрия. – М. – Л.:   Гостехиздат, 1949. – 512 с.

6        Долгарев А.И. Евклидова кривая в сопровождающем репере. – Вестник Татарского государственного гуманитарно-педагогического университета. – Казань, 2010, вып. 2(20). – С. 2 – 19.

7        Фиников С.П. Курс дифференциальной геометрии. Изд. 2. – М.: КомКнига, 2006. – 344с.

8        Долгарев А.И. Редукция к каноническим евклидовым кривым в естественной параметризации. - Materialy VIII Miedzynarodowej naukowi-praktycznej konferenceji “Wschodnie partnerstwo – 2012” 07 – 15 wrzesnia 2012 roku. Volume 12. Matematika, Fizika, Novoczesne informacyjne technologie, Techniczne nauki. – Przemysl: Nauka i studia 2012, p. 15 – 24.

9        Вейль, Г. Пространство. Время. Материя. Лекции по общей теории относительности.  – М.: Едиториал УРСС, 2004. – 456 с.                     

10    Долгарев А.И. Натуральные уравнения кривых 3-мерных одулярных галилеевых пространств// Дифференциальная геометрия многообразий фигур. Межвуз. тем. сб. научн. тр. Вып. 36. – Калининград: КГУ, 2005. – С. 31 – 36.

11    Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967. - 664с.

12    Долгарев А.И. О геометрии 3-мерного действительного многообразия. – Вестник Татарского государственного гуманитарно-педагогического университета. – Казань, 2010, вып. 1(23). – С. 2 – 19.

13    Долгарев А.И., Долгарев И.А. Некоторые приложения галилеевых методов. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, Пенза: ИИЦ ПГУ, 2009, № 2(9), с. 39 – 59.

14    Долгарев А.И., Долгарев И.А. Неоднородность пространственной составляющей пространства-времени.  – Материали за VIII Международна научна практична конференция «Новини на научния прогрес – 2012» 17 – 25 август 2012 г. Том 9. Математика. Съвременни технологии на информации. – София: Бял ГРАД-БГ ООД 2012, с. 29 – 39.

15    Долгарев А.И. Структура галилеева пространства-времени. - Materialy VIII mezinarodni vedecko-praktika conference «Aplikovane vedecke novinky – 2012»  Dil 12. Matematika, Fizika, Novoczesne informacyjne technologie. – Praha: Publishing House “Education and Science” s.r.o. 2013, p. 13 – 21.

15    Арнольд В.И. Математические методы классической механики. – М.: Наука, 1989.– 472с.

16    Долгарев А.И. Различные по Ф. Клену евклидовы геометрии: элементарная и диф-      ференциальная.// Materialy IX Miedzynarodowej naukowi-praktycznej konferencji       “Strategiczne pytania swiatowej nauki – 2013” Volume 28. Matematyka. Fizyka.       Nowoczesneinformacyjne technologie.: Przemysl. Nauka i studia – 2013,  C. 3 – 8.

  1. Долгарев А.И. Натуральные уравнения галилеевой кривой и решение уравнения Ньютона для движения с двумя степенями свободы.// Материали за VII Международна научна практична конференция «Найновите  постижения на европейската наука» – 2011. Том 37. Математика. София. «Бял ГРАД-БГ» ООД 2011. – С. 5 – 15.
  2. Долгарев А.И. Решение задачи Ньютона для движения с тремя степенями свободы.- Materialy VIII mezinarodni vedecko-praktika conference “Veda a vznik – 2011 - 2012”. Dil 28. Matematika,Fizika, Moderni informacni technologie. Praga,2012, p. 3 – 8.
  3. Долгарев А.И. Определяемость евклидовой кривой вектором галилеевой кривизны.// Materialy IX Miedzynarodowej naukowi-praktycznej konferencji “Dinamika naukowych badan – 2013” Volume 12. Matematyka. Fizyka. Nowoczesne informacyjne technologie. Chemia i chemiczne technologie: Przemysl. Nauka i studia – 2013, C. 29 – 37.