Математика/ 5. Математическое моделирование

к.ф.-м.н. Искакова А., Утеумагамбетова Н.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Об одном методе комбинаторного исследования количества сочетаний вариантов с наложением определенных условий

Изучение комбинаторного анализа определяется потребностями практики. Так, например, для успешной разработки педагогических заданий в тестовой форме полезно знать максимальное количество всевозможных вариантов тестов с невозможным совпадений заданий.

Рассмотрим следующую задачу. Из имеющейся базы вопросов составить максимальное число индивидуальных вариантов тестов. Структура базы данных следующая: код предмета, код раздела, код темы, код подтемы, номер вопроса, сложность вопроса и сам вопрос.

По имеющейся базе данных необходимо составить варианты тестовых заданий с учетом следующих условий:

1. Вариант теста должен включать в себя определенное количество вопросов с каждого раздела.

2. Структура теста должна состоять из некоторого числа вопросов первой, второй и третьей сложностей.

3. В одном варианте теста использование вопросов с одной подтемы не должно превышать единицы.

Рассмотрим три случая:

1. Вычисление максимального числа индивидуальных вариантов теста, учитывая определенное количество вопросов с каждого раздела.

2. Вычисление максимального числа индивидуальных вариантов теста, учитывая определенных количеств вопросов первой, второй и третьей сложностей.

3. Вычисление максимального числа индивидуальных вариантов теста, учитывая все налагаемые условия, а именно, учитывая определенное количество вопросов с каждого раздела, определенных количеств вопросов первой, второй и третьей сложностей и использование вопросов с одной подтемы не должно превышать единицы.

Допустим, имеем k разделов. В первом случае число индивидуальных вариантов теста, учитывая определенное количество вопросов с каждого раздела определяется с использованием формулы числа сочетаний:

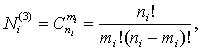
где i – порядок раздела, n_i - количество всех вопросов i – го раздела, вне зависимости от сложности, m_i - количество вопросов, необходимое с i – го раздела.

После вычисления количества вариантов для каждого раздела, используем правило умножения и выводим результат, равный максимальному числу индивидуальных вариантов теста для данного случая:

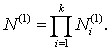
Во втором случае число индивидуальных вариантов теста, учитывая числа вопросов первой, второй и третьей сложностей определяется по средством следующего алгоритма. Пусть S₁, S₂ и S₃ – количество вопросов соответственно первой, второй и третьей сложности, вне зависимости от раздела, s₁, s₂ и s₃ – количество вопросов соответственно первой, второй и третьей сложности, необходимых в варианте теста. Тогда максимальное значение количества вариантов теста, учитывая числа вопросов первой, второй и третьей сложностей определяется как

При определении максимального числа индивидуальных вариантов теста, учитывая все налагаемые условия, а именно, учитывая определенное количество вопросов с каждого раздела и определенных количеств вопросов первой, второй и третьей сложностей используем следующие действия.

Учитывая определенное количество вопросов с каждого раздела определяется с использованием формулы числа сочетаний:

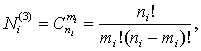
где i – порядок раздела, n_i - количество всех вопросов i – го раздела, вне зависимости от сложности, m_i - количество вопросов, необходимое с i – го раздела. Тогда максимальное значение количества вариантов теста, учитывая налагаемые условия

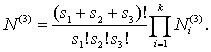
Таким образом, с использованием комбинаторных формул решена задача количества варьирования всевозможных вопросов с учетом налагаемых условий.

Список литературы

1. Н.М. Опарина, Г.Н. Полина, Р.М. Файзулин, И.Г. Шрамкова. Адаптивное тестирование : учеб.-метод. пособие / Н. М. Опарина              [и др]. – Хабаровск : Изд-во ДВГУПС, 2007. – 95. : ил.

2. Я. Виленкин, Комбинаторика, Москва, Наука, 1969.

3. Н. Б. Алфутова, А. В. Устинов, Алгебра и теория чисел (сборник задач), Москва, МЦНМО, 2002.

4. Дж. Риордан, Введение в комбинаторный анализ, Москва, ИЛ, 1963.

5. М. Холл, Комбинаторика, Москва, Мир, 1970.

6. Р. Стенли, Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции, Москва, Мир, 2005.

7. В. Феллер, Введение в теорию вероятностей и ее приложения, Москва, Мир, 1967.

8. М. Б. Лагутин, Наглядная математическая статистика, Москва, Бином. Лаборатория знаний, 2007.