Математика/5. Математическое моделирование

Аманбаев Т.Р., Мамешов Б.

Южно-Казахстанский университет им. М. Ауэзова, Казахстан

Моделирование течений дисперсной среды при наличии процессов нуклеации, коагуляции и фазовых превращений

В практике часто встречаются процессы, в которых в исходном состоянии рабочая среда является однофазной, например, в виде газа (пара), а в ходе исследуемого процесса создаются условия для появления новой фазы в виде капель [1]. Именно этими процессами определяется начальная стадия фазовых переходов в однофазных (в исходном состоянии) средах (например, в переохлажденном паре). Появившиеся в результате нуклеации зародыши жидкой фазы являются достаточно мелкими (наноразмерными) и в связи с этим подвержены броуновскому блужданию. Броуновское блуждание приводит к их взаимному столкновению, поэтому является одним из основных, постоянно действующих механизмов, способствующих коагуляции микрокапель.

В данной работе рассматривается течение смеси газа и зародышей жидкой фазы в квазиодномерном приближении, когда поперечными градиентами параметров среды можно пренебречь. Рассмотрим простейший случай, когда внешние силы, поток тепла извне и трение со стенкой отсутствуют. Допустим, что на входе в канал однофазная среда находится в переохлажденном состоянии, когда температура среды ниже температуры насыщения. Будем считать, что процесс конденсации в метастабильном состоянии пара протекает в две стадии. На первой стадии за счет гомогенной нуклеации появляются зародыши жидкой фазы. Некоторые из них исчезают, а некоторые (размеры которых превышают критического радиуса) растут в дальнейшем за счет броуновской коагуляции и фазовых превращений (конденсации). Ввиду малости размеров зародышей, можно считать, что скорости и температуры дисперсной и несущей фаз совпадают.

Таким образом, для описания рассматриваемого течения в стационарном случае имеем следующую систему уравнений

, , , (1)

, (2)

, ; , ,

Здесь нижние индексы 1 и 2 относятся к параметрам газовой и конденсированной фаз соответственно; -истинная и приведенная плотности, объемное содержание и энтальпия фаз; v, p, n, a -скорость и давление в газе, а также концентрация и радиус зародышей; x, S(x) - продольная координата и площадь поперечного сечения канала; -интенсивность фазового перехода, -коэффициент броуновской коагуляции кластеров, -температура пара, -постоянная Больцмана, -вязкость пара.

Зададим уравнения состояния фаз: газ будем считать калорически совершенным с постоянной теплоемкостью, а вещество конденсированной фазы – несжимаемым. Тогда будем иметь

, , (3)

,

где , - теплоемкости газа и дисперсной фазы; R – газовая постоянная; , , , - параметры среды в некотором фиксированном (например, начальном) состоянии, относительно которого отсчитываются все изменения.

Зависимость температуры насыщения фаз от давления удовлетворяет дифференциальному уравнению Клапейрона–Клаузиуса [1]:

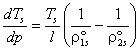(4)

Здесь и - температура насыщения и теплота парообразования.

Кинетика фазового перехода описывается уравнением Герца–Кнудсена–Ленгмюра [1]:

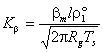, (5)

где –коэффициент аккомодации. Интенсивность фазового перехода равна

, (6)

В чистом пересыщенном паре начальное состояние метастабильно и процесс конденсации начинается только при появлении зародышей жидкой фазы, имеющих размер больше некоторого критического (гомогенная нуклеация). Молекулярно-кинетическая теория процесса гомогенной нуклеации была заложена в работах ряда исследователей (см. [1, 2]). Эта теория основана на том, что в газе в результате флуктуаций концентрации молекул в их хаотическом движении беспрерывно образуются и разрушаются кластеры (микрокапли в переохлажденном паре). Флуктуационное зародышеобразование и дальнейший конденсационный рост кластеров в пересыщенном паре является одним из наиболее важных процессов, приводящих к зарождению и развитию дисперсной фазы. Далее будут рассматриваться только сферические кластеры, в которых число молекул однозначно связано с их радиусом

₍ - масса одной молекулы газа, a – радиус кластера). В случае максвелловского распределения молекул по скоростям распределение указанных кластеров по радиусу описывается известной формулой Гиббса

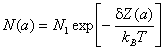
где - число молекул несущей фазы в единице объема, - так называемая работа создания кластера радиусом a. Работа равна изменению термодинамического потенциала Гиббса для вещества, входящего в кластер с учетом вклада для создания поверхности жидкой фазы

,

Здесь z-потенциал Гиббса, σ-свободная энергия межфазового взаимодействия на единицу поверхности (поверхностное натяжение). В метастабильном состоянии, когда (переохлажденный пар или перегретая жидкость) имеет максимум при

,

Величина называется критическим радиусом зародыша, а величина - работой создания критического зародыша. Таким образом, если в метастабильной несущей фазе возникает кластер с размером , то оно должно расти, так как это приводит к уменьшению термодинамического потенциала системы. Докритические кластеры с радиусом должны исчезать, поскольку это также приводит к уменьшению термодинамического потенциала. Отсюда следует, что появление жизнеспособных зародышей связано с преодолением потенциального или активационного барьера . Используя линейное разложение потенциала Гиббса около состояния насыщения вдоль изотермы для переохлажденного пара получим [1]:

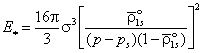, , (7)

где , - истинные плотности газовой и жидкой фаз в состоянии насыщения. Концентрация критических зародышей определяется по формуле

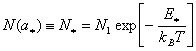(8)

Можно представить следующую последовательность процесса кластеризации дисперсной фазы [3]. Начало фазового перехода определяется вероятностью возникновения зародышей именно критического размера, в связи с чем, при расчете кластеризации учитывается образование только этих зародышей. Число зародышей критического размера велико и составляет примерно 10¹⁹ зародышей в единице объема, и поэтому, несмотря на их малый размер ( м), общая поверхность, на которой происходит конденсация, достаточно велика. За счет быстрого образования зародышей и их дальнейшего роста происходит интенсивное увеличение массы жидкой фазы и выделение тепла. Выделение тепла приводит к уменьшению степени перенасыщения, в результате чего образование новых зародышей прекращается, и в дальнейшем кластеризация идет уже на образовавшихся зародышах. Переход от метастабильного состояния в состояние насыщения может произойти довольно быстро и носить скачкообразный характер. Отсюда следует, что процесс кластеризации в высокоскоростных потоках можно разделить на две стадии. На первой стадии определяющим является процесс образования зародышей критического размера, на второй – процесс конденсационного роста уже образовавшихся зародышей, когда нуклеацию можно не учитывать. Хотя в ряде случаев одновременно протекают оба процесса, такое разделение представляется вполне разумным.

Таким образом, принимая во внимание вышеуказанные обстоятельства, на входе в канал зададим следующие начальные условия:

x=0, , , , , , , (9)

Система уравнений (1), (2) с замыкающими соотношениями (3)-(8) и начальными условиями (9) представляет задачу Коши для расчета течения газа в канале переменного сечения при наличии процессов нуклеации, коагуляции зародышей (кластеров) и фазовых переходов.

Литература

1. Нигматулин Р.И. Динамика многофазных сред. Т.1. М: Наука, 1987. 464 с.

2. Зельдович Я.Б. Химическая физика и гидродинамика. М.: Наука, 1984. 374 с.

3. Модели образования наночастиц в потоках газа. Курс лекций. (do.nano.fcior.edu.ru/).