МНОГОКРИТЕРИАЛЬНЫЕ АдаптивныЕ алгоритмЫ Для тестирования знаний

Гданский Н.И., Рысин М.Л., Альтиментова Д.Ю.

Предложены адаптивные алгоритмы тестирования знаний, которые могут одновременно автоматически подстраиваться для решения задач проверки знаний по нескольким параметрам

Потребность использования адаптивных алгоритмов тестирования знаний вызвана широким распространением компьютерных обучающих систем. Для достижения реального эффекта при проверке знаний данные системы должны автоматически адаптироваться к процессу тестирования по целому ряду параметров.

Оптимальным является модульный принцип построения структуры содержательной части учебных материалов, при котором они разделены на систему взаимосвязанных модулей – частей курса, освещающих отдельные законченные его темы. Каждый модуль содержит все необходимые теоретические сведения, а также примеры решения всех необходимых видов практических заданий. Важной составляющей информационных материалов являются вопросы для самостоятельной проверки знаний. С одной стороны, их формирование позволяет преподавателю оценить информационную корректность материала, изложенного в модуле. С другой стороны, их содержание должно помочь студенту подготовиться к выполнению тестовых материалов.

Тестирование знаний является отдельной многоплановой областью педагогики, призванной решать целый ряд задач по проверке знаний [1]. Выбор типа, структуры и содержания тестов может осуществляться многими способами. Оптимальные решения во многом зависят от цели тестирования, вида излагаемого материала, уровня подготовки учащихся, требованиям к уровню освоения дисциплины и других факторов.

С целью сохранения модульной структуры представления знаний в обучающей системе в качестве минимальной тестируемой единицы изучаемой дисциплины также необходимо принимать модуль.

В электронных обучающих системах тестирование по назначению подразделяется на два основных вида:

1) учебное, которое выполняется студентами самостоятельно для оценки знаний самим обучающимся,

2) контрольное, выполняемое для контроля авторизации под наблюдением преподавателя в целью объективной оценки реального уровня знаний.

Практически данные возможности обеспечиваются применением двух различных алгоритмов тестирования. Учебное тестирование всегда выполняется только по модулям. Результаты анализа ответов на каждый теоретический вопрос или решение каждой задачи оперативно объявляются учащемуся. Также в результате анализа текущих ответов формируется траектория контроля - выбирается число и содержание очередных вопросов и практических заданий. После завершения учебного тестирования выставляется общая оценка в баллах и, если необходимо, общие рекомендации по повторному изучению материала.

Контрольное тестирование может выполняться по подразделам, разделам и всему курсу – в зависимости от запроса преподавателя, проводящего проверку знаний. Для сокращения времени опроса текущие результаты контроля не объявляются учащемуся. В конце опроса выставляется общая оценка в баллах.

В государственных образовательных стандартах постоянно наращивается доля самостоятельной работы в общей учебной нагрузке студентов вузов. В этих условиях применение автоматизированных систем обучения является одним из наиболее эффективных механизмов активизации и реального наполнения той части самостоятельной работы студентов, которая предназначена на подготовку к тем или иным видам занятий по изучаемой дисциплине.

В общем случае тестирование знаний учащихся в электронных учебных курсах можно подразделить следующим образом:

1) по цели тестирования – на учебное и контрольное,

2) по охвату проверяемого материала – на тестирование по модулям, разделам и всей дисциплине,

3) в зависимости от состава тестирующих материалов – одноуровневое, двух уровневое и трехуровневое тестирование.

Адаптивная система тестирования помимо адаптации к пунктам 1) - 3) также должна адаптироваться к уровню знаний студента, выполняющего тесты, с целью более полного его выявления. Рассмотрим предлагаемый подход к ее построению.

Каждый тестирующий блок подраздела содержит базовый набор из 20-30 вопросов для проверки теоретических знаний. Если тестируется обзорный материал, не содержащий глубоких теоретических выкладок либо методов решения задач, то данный материал является достаточным для проверки знаний. Такое тестирование назовем одноуровневым.

Если же подраздел содержит теоретические материалы и/или методику решения задач, то базовый тестирующий раздел в зависимости от содержания учебного материала целесообразно дополнить следующими материалами: 1) теоретическими вопросами повышенной сложности, 2) задачами, 3) задачами повышенной сложности. В сумме число k предлагаемых видов тестирующих материалов по подразделу на практике не должно превышать 3. В зависимости от числа k предлагаемых уровней тестирования (1,2 или 3) соответствующая схема тестирования названа 1-, 2- и 3-уровневой. Для более эффективной проверки знаний тестирование по разным уровням должно выполняться последовательно в порядке возрастания сложности материала, проверяемого на отдельных уровнях.

Для адаптации процесса тестирования к уровню подготовки студента предложено выделить на каждом уровне 2 фазы опроса:

1) основную (обязательную), на которой задаются начальные тестовые задания и

2) уточняющую (необязательную), на которой задаются дополнительные тестовые задания, позволяющие уточнить знания студента на текущем проверяемом уровне.

Общим принципом адаптации процесса тестирования на текущем уровне к степени подготовки учащегося предложено принять следующее правило: если число правильных ответов в основной фазе опроса не превышает половины (недостаточный уровень знаний), то производится уточнение знаний на текущем уровне, если число правильных ответов больше половины (высокий уровень знаний), то осуществляется переход к основному опросу на следующем более высоком уровне.

Для графической иллюстрации стратегии опроса и оценивания знаний предложено использовать t-деревья, где t – базовое (минимальное) число тестовых заданий основной фазы опроса по одному модулю при тестировании всей дисциплины. Данное число минимально и составляет основу расчета числа тестовых заданий модуля при проверке одного раздела и одного данного модуля. Количество базовых тестовых заданий t необходимо задавать с учетом специфики проверяемого предмета и сложности тестовых заданий.

Рассмотрим потенциальные возможности предлагаемого алгоритма по его адаптации к рассмотренным выше факторам.

1. Адаптацию к цели тестирования (учебное или контрольное) предлагается осуществлять за счет формы оценки результатов выполнения тестов, выдачи результатов выполнения тестов студенту или передачи их преподавателю и т.д.

2. Адаптацию к охвату проверяемого материала предлагается производить путем кратного увеличения числа основных тестовых заданий t в случае дисциплинарного охват. При тестировании раздела (охват по разделу). предлагается применять число основных тестовых заданий по модулям, равное t×k_p, при тестировании только одного модуля (модульный охват) число основных тестовых заданий по нему принимаем равным t×k_м. Коэффициенты k_p и k_м – целые числа. Их величины следует выбирать с учетом сложности и характера тестируемого учебного материала.

3. Адаптация к составу тестирующих материалов производится путем выбора числа уровней в соответствующем t-дереве.

4. Адаптация к уровню подготовки студентов осуществляется при помощи самой структуры t-дерева алгоритма тестирования, учитывающей различные сценарии развития тестирования.

Рассмотрим построение деревьев опроса на примере 1- и 2-уровневого тестирования. Для простоты примем число тестовых модульных заданий t при тестировании всей изучаемой дисциплины, равное 2. Коэффициент k_p примем равными: k_p = 2.

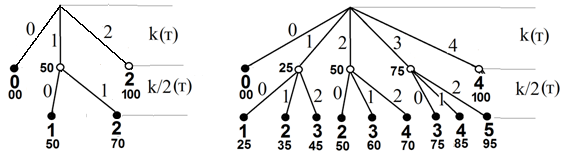
1-уровневое тестирование. При заданных параметрах процесса тестирования алгоритм одноступенчатого тестирования проиллюстрирован на дереве опроса на рис.1а,б. Рис.1а задает схему алгоритма для дисциплинарного охвата тестирования при t =2, рис. 1б – для -охват по разделу при t =2, k_p = 2. На схеме черными точками показаны листья дерева, обозначающие завершение тестирование, белами – промежуточные вершины, в которых тестирование еще не завершено. Рядом с листьями указано число правильных ответов и начисленная сумма баллов.

а б

Рис.1. Схема алгоритма одноступенчатого тестирования

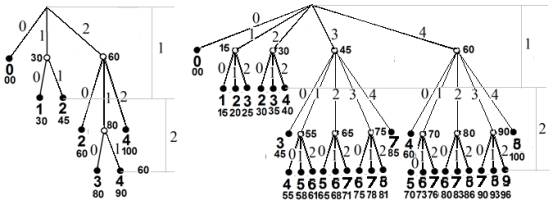
2-уровневое тестирование. При задании распределения общей суммы баллов на первой и второй ступенях в отношении 60:40 получаемый алгоритм двухступенчатого тестирования проиллюстрирован на 2-дереве опроса при t=2 и k_p = 2 на рис.2а,б. Рис.2а задает схему алгоритма для дисциплинарного охвата при t =2, рис. 2б – для охвата по разделу при t =2, k_p = 2.

а б

Рис.2. Схема алгоритма 2-уровневого тестирования с параметрами t =2, k_p = 2

Как видно из рис.1 и 2, графическое задание алгоритмов тестирования является наглядным и удобным для понимания его работы, однако получаемые изображения громоздки и неудобны при программировании методов на его основе. Сходный алгоритм выполнения тестирования на разных уровнях, а также накопительный принцип образования суммарной суммы баллов позволяют использовать для записи и программирования конкретных вариантов алгоритма одинаковую унифицированную процедуру.

Допустим, необходимо представить общий алгоритм тестирования, использующий t тестовых модульных заданий с коэффициентом k, при общем числе уровней тестирования N, причем распределение баллов по уровням задано массивом P[1:N]. Множество параметров такого процесса имеет вид {t, k, N, P[1:N]}. Работу общего алгоритма тестирования можно представить как последовательное применение одной и той же элементарной процедуры Тест одноуровневого тестирования с параметрами {t, k, i, Pi, Ri , Ti}, где i - номер уровня, Ri - число полученных правильных ответов, Ti - число баллов, начисленных на данном уровне тестирования. Блок-схема элементарного алгоритма тестирования Тест дана на рис.3.

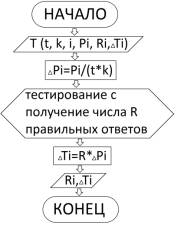
Рис.3. Блок-схема элементарного алгоритма тестирования Тест

Обозначая через Тi количество баллов, получаемое учащимся при тестировании модуля с параметрами {t, k, Pi}на уровне i, общий результат тестирования по данному модулю можно представить в виде скалярной суммы баллов по каждому уровню тестирования:

Т= Т1+ Т2+…+ ТN, (1)

либо в виде вектора:

`Т=(Т1,Т2,…,ТN). (2)

Рациональную форму итогового представления необходимо выбирать в каждом отдельном случае с учетом особенностей материала тестов. При близком характере тестирования по отдельным уровням (например, разные уровни теоретического материала) можно применять скалярную формулу (1). При значительных различиях тестового материала на различных уровнях (например, теоретические вопросы - задачи) более логично использование векторной формы (2). В соответствии с выбранной формой итогового представления результатов тестирования (1) или (2) им можно задать пространственную интерпретацию в пространстве значений признаков и выполнять их сравнительный анализ.

С учетом предложенного принципа учета знаний учащегося в процессе тестирования блок-схему общего алгоритма тестирования можно представить в виде, данном на рис.4.

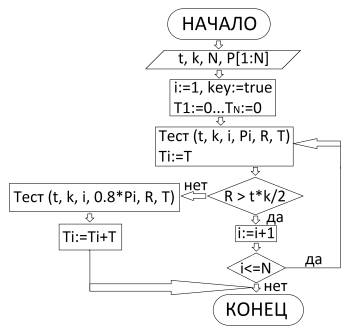
Рис.4. Блок-схема общего алгоритма тестирования

В целом предлагаемая организация контента в информационно-тестирующей системе и дополнение стандартной LMS набором программ-анализаторов позволит не только освободить преподавателя от большого объема рутинной работы, но и сделать учебный процесс более предсказуемым, динамичным и управляемым, привить как студентам, так и преподавателям, навыки активного взаимодействия с информационными ресурсами современного уровня, органично дополняющими традиционным формам обучения. Во многом это позволит решить вопросы организации самостоятельной работы, которые довольно остро ставит перед вузами переход на учебные стандарты третьего поколения.

Библиографический список

1. Свиридов А.П. Статистическая теория обучения. – М., Издательство РГСУ,2009. – 576 с., илл 131, библ.- 398 назв.