Педагогічні науки / 5. Сучасні методи
викладання
К.п.н. Ачкан В.В., Заяць Н.В.
Бердянський
державний педагогічний університет
Інноваційні аспекти підготовки
учнів основної школи до державної підсумкової атестації з математики
Сучасний етап розвитку національної освіти
характеризується тим, що освіта має бути інноваційною, тобто повинна постійно
змінюватися i сприяти формуванню особистості, здатної до сприйняття змін
упродовж життя, яка може застосовувати набуті знання в практичній діяльності. З огляду на це важливою проблемою є
розробка теоретичних основ створення педагогічних
нововведень, їх оцінки і використання на практиці для реалізації вимог нових
освітніх стандартів.
Державна
підсумкова атестація (ДПА) з математики стала невід’ємним атрибутом закінчення
навчального процесу в основній школі. Тому підготовка учнів до її проходження є
актуальною та достатньо гострою проблемою.
Нами розроблені методичні рекомендації, щодо
організації уроків систематизації та узагальнення знань і вмінь старшокласників
із змістової лінії рівнянь та нерівностей та теми тотожні перетворення виразів,
спрямовані на формування їх математичних компетентностей, успішне виконання
завдань ДПА. Ця робота проводиться за рахунок 10 годин, що виділені
на систематизацію та узагальнення знань і вмінь учнів у 9 класі (для
загальноосвітніх класів) та 15 годин – для класів з поглибленим вивченням
математики, у вигляді систематизуючих бесід за наступними темами: виконання
тотожних перетворень у ДПА з математики; розв’язування рівнянь та нерівностей
у ДПА з математики; розв’язування текстових задач у ДПА з математики.
До інноваційних аспектів цієї
підготовки ми відносимо виділення для учнів узагальнених орієнтовних основ
діяльності з виконання тотожних перетворень; розв’язування рівнянь, нерівностей
та їх систем; розв’язування текстових задач та використанню ІКТ не тільки на
етапі повторення та систематизації теоретичного матеріалу, але й під час
формування здатності розв’язувати певні види завдань. Зрозуміло, що під час
ДПА учні не зможуть використати комп’ютер, проте, з метою активізації
навчальної діяльності учнів, економії часу та залучення до роботи учнів, що
знаходяться на середньому рівні навчальних досягнень при підготовці до ДПА,
доцільно використовувати ІКТ, зокрема ППЗ “GRAN1” під час розв’язування окремих
завдань. Наприклад, виконуючи завдання атестаційної роботи № 32 [1] (знайдіть значення параметру а, при якому система 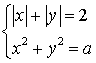 має рівно
чотири розв’язки) учні спочатку вдаються до аналітичних міркувань. Друге рівняння не має
розв’язків при а < 0, адже ліва
його частина завжди невід’ємна. Легко також побачити, що при а = 0 розв’язок першого рівняння (0;0)
не є розв’язком другого. Отже, треба побудувати графіки обох рівнянь системи та
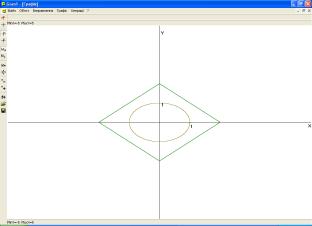
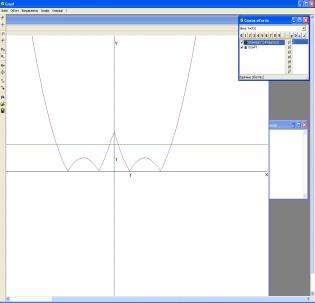
визначити, при яких додатних значеннях параметра а вони перетинаються в чотирьох точках. Учні будують у ППЗ “GRAN1” графіки заданих в неявному вигляді функцій
має рівно
чотири розв’язки) учні спочатку вдаються до аналітичних міркувань. Друге рівняння не має
розв’язків при а < 0, адже ліва
його частина завжди невід’ємна. Легко також побачити, що при а = 0 розв’язок першого рівняння (0;0)
не є розв’язком другого. Отже, треба побудувати графіки обох рівнянь системи та
визначити, при яких додатних значеннях параметра а вони перетинаються в чотирьох точках. Учні будують у ППЗ “GRAN1” графіки заданих в неявному вигляді функцій ![]() та
та ![]() (рис. 1, 2). За
допомогою графіка учні доходять висновку, що коло з центром у точці (0; 0) і
радіусом а, яке утворює графік
функції
(рис. 1, 2). За
допомогою графіка учні доходять висновку, що коло з центром у точці (0; 0) і
радіусом а, яке утворює графік
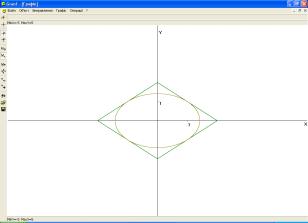
функції ![]() та квадрат, що
утворює графік функції
та квадрат, що
утворює графік функції ![]() мають чотири точки
дотику у двох випадках (рис. 2, 3).
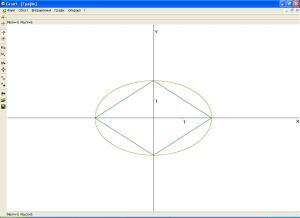
мають чотири точки
дотику у двох випадках (рис. 2, 3).
Отже система має чотири розв’язки
при двох значеннях параметру а:
а = 2 та а = 4. Після розв’язування даного рівняння доцільно сформулювати за
допомогою учнів наступний орієнтир: перш
ніж розв’язувати подібні системи, доцільно проаналізувати, при яких значеннях
параметра система може мати розв’язки. Потім доцільно використати графічний
метод розв’язування. При цьому графічна ілюстрація
може використовуватися як для безпосереднього знаходження розв’язків чи
відповіді на питання задачі (у разі, якщо шукане значення є цілим числом), так
і як допоміжний засіб для аналітичних міркувань (у разі, якщо шукане значення є
дробовим числом).
|
Рис. 1 Графіки функцій |
Рис. 2. Графіки функцій |
|
|
|
Розглянемо розв’язування завдання
атестаційної роботи № 49 [1]: при яких
значеннях параметра а рівняння ![]() має шість розв’язків?
Учні будують графіки функцій
має шість розв’язків?
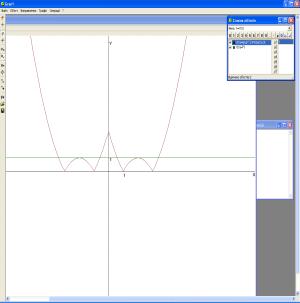
Учні будують графіки функцій ![]() та g(x)
= a у ППЗ GRAN1 (рис. 4) та
змінюють значення параметру, шукаючи те, при якому графіки цих функцій
перетинаються у шести точках. Учні переконуються що пряма g(x) = a та графік функції
та g(x)
= a у ППЗ GRAN1 (рис. 4) та
змінюють значення параметру, шукаючи те, при якому графіки цих функцій
перетинаються у шести точках. Учні переконуються що пряма g(x) = a та графік функції ![]() мають шість точок
перетину лише при а = 1. Аналіз
побудованого у ППЗ GRAN1 графіка функції
мають шість точок
перетину лише при а = 1. Аналіз
побудованого у ППЗ GRAN1 графіка функції ![]() дозволяє допомогти
навіть учням, що навчаються на середньому рівні навчальних досягнень, зрозуміти
алгоритм побудови та побудувати цей графік у зошитах. Вчитель звертає увагу
учнів на те, що функція
дозволяє допомогти
навіть учням, що навчаються на середньому рівні навчальних досягнень, зрозуміти
алгоритм побудови та побудувати цей графік у зошитах. Вчитель звертає увагу
учнів на те, що функція ![]() є парною, оскільки f(x)
= f(-x). Таким чином, спочатку доцільно побудувати її графік для
є парною, оскільки f(x)
= f(-x). Таким чином, спочатку доцільно побудувати її графік для ![]() Підмодульна функція
Підмодульна функція ![]() є параболою, вітки
якої направлені вгору, що проходить через точки (0;3), (1;0), (3;0) з вершиною
у точці (2;
є параболою, вітки
якої направлені вгору, що проходить через точки (0;3), (1;0), (3;0) з вершиною
у точці (2; ![]() 1). Відобразивши симетрично осі абсцис від’ємні значення
параболи, отримаємо графік функції
1). Відобразивши симетрично осі абсцис від’ємні значення
параболи, отримаємо графік функції ![]() для
для ![]() Відобразивши
симетрично отриманий графік відносно осі ординат, отримаємо загальний вигляд
графіка функції
Відобразивши
симетрично отриманий графік відносно осі ординат, отримаємо загальний вигляд
графіка функції ![]()
|
Рис. 2.9. Графіки функцій g(x) = a та |
Рис. 2.10. Графіки
функцій g(x)
= a та |
Після розв’язування даного рівняння доцільно сформулювати за допомогою
учнів наступний орієнтир: якщо за умовою
завдання вимагається знайти кількість коренів рівняння, то доцільно
застосовувати графічний метод розв’язування.
Результати
навчання за розробленою методикою показали, що проведення трьох систематизуючих
бесід, в основу систематизації матеріалу яких лягли основні методи виконання
тотожних перетворень, розв’язування рівнянь, нерівностей та їх систем, розв’язування
текстових задач, використання ІКТ на етапі формування орієнтовних основ
діяльності сприяло закріпленню в учнів відповідних математичних
компетентностей, правильному, свідомому та чіткому розв’язуванню ними завдань
державної підсумкової атестації.
Література
1.
Збірник завдань
для державної підсумкової атестації з математики. 9 клас / [О.І. Глобін, О.В. Єргіна,
П.Б. Сидоренко, О.В. Комаренко]. – К. : Центр навчально-методичної літератури, 2013.
– 166 с.
2.
Наказ МОН
України від 05.05.2008 № 371. – [Електронний ресурс]. – Режим доступу: – www.mon.gov.ua/laws/MON_371_08.doc
3.
Неліна О.Є.
Систематизація та узагальнення знань і вмінь учнів з алгебри як засіб
активізації їх пізнавальної діяльності : дис. ... кан. пед. наук : 13.00.02 “Теорія
і методика навчання (математика) ”/ Неліна Оксана Євгенівна. – Х., 2003 – 241
с.