Технічні науки/ Автоматизовані
системи управління на виробництві
М.П. Лисиця, П.М.
Лисиця, О.В. Лисиця
Полтавський національний технічний університет ім.
Ю. Кондратюка
Адаптивне
керування системою з еталонною моделлю в умовах невизначеності
При наявності параметричної та
сигнальної невизначеності в об’єктах керування, які описуються передавальною
функцією
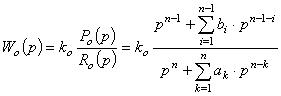
в безпошукових адаптивних системах, функціонуючих за
еталонною моделлю
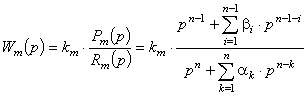 ,
,
де і = 1, 2…n - 1, k = 1, 2…n, ![]() - строго дійсно додатна, при керуванні за
виходом ставиться задача необхідності забезпечення виконання умови глобальної
стійкості і прямування похибки
- строго дійсно додатна, при керуванні за
виходом ставиться задача необхідності забезпечення виконання умови глобальної
стійкості і прямування похибки ![]() до нуля
до нуля
![]() ,
, ![]() .
.
В алгоритмі керування і адаптації
за виходом використовуються не тільки доступні для вимірювання сигнали
(задавальна дія, вхідні та вихідні сигнали), а і сигнали, отримані шляхом
спеціальної фільтрації.
Векторні сигнали, отримані шляхом такої
фільтрації вхідного сигналу керування u
і вихідного сигналу y,
які записані диференціальними рівняннями в формі Коші ![]() ,
, ![]() , мають вигляд:
, мають вигляд: ![]() ,
, ![]() .
.
Матриці ![]() ,
, ![]() та F сформовані наступним чином:
та F сформовані наступним чином:
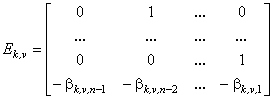 ,
, 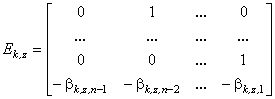 ,
, 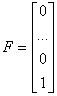 ,
,
де ![]() , а
, а ![]() ,
, ![]() - спеціальним чином підібрані поліноми.
- спеціальним чином підібрані поліноми.
Робастне
адаптивне керування системою з еталонною моделлю при коригуванні вектора
вимірюваних сигналів виконано за наступними формульними співвідношеннями:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
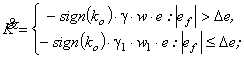
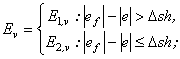
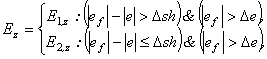
де ![]() ,
, ![]() - відфільтроване та порогове значення похибок;
- відфільтроване та порогове значення похибок; ![]() - порогове значення шумової похибки.
- порогове значення шумової похибки.
На рис. 1
наведено структурну схему керування об’єктом другого порядку, а на рис. 2 - зміну параметрів об’єкта та сигналів у каналі
вимірювання і на виході об’єкта коригованої та
не коригованої системи керування.
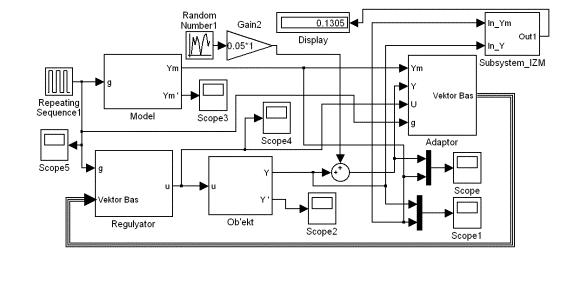

Рис. 1. Структурна
схема адаптивної системи керування об’єктом другого порядку
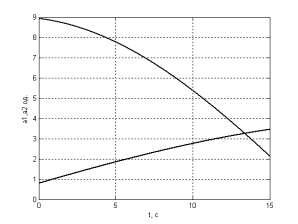

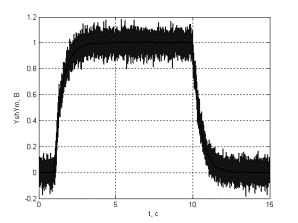

а б
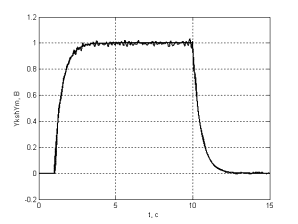



в г
Рис. 2. Часові
діаграми: а) зміни параметрів об’єкта; б) вихідних сигналів у каналі
вимірювання; в) вихідних сигналів об’єкта коригованої системи керування; г) вихідних
сигналів об’єкта не коригованої системи керування
Дослідження
динаміки роботи наведеної адаптивної системи в середовищі комп’ютерного
моделювання MATLAB для об’єкта другого
порядку показало, що при ефективному шумовому сигналі вимірювача вихідного
параметра 3s=0,15×уust та зміні
коефіцієнтів об’єкта а1 і а2 в чотири рази досягнуто
зменшення результуючої похибки системи у вісім разів.
Література:
1. Методы классической и
современной теории автоматического управления: учебник в 3-х т.− Т.3.
Методы современной теории автоматического управления/ под ред. Н. Д.
Егупова.− М.: Изд-во МГТУ им. Н. Е. Баумана, 2000.− 748 с.