Лебедев Е

Лебедев Е.П., Веренич И.А.

Белорусский национальный технический университет, г. Минск

КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ В МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ СОПЛА ЛАВАЛЯ

Сопло Лаваля это газовый канал особого профиля, разгоняющий проходящий по нему газовый поток до сверхзвуковых скоростей. Оно используется на некоторых типах паровых турбин и является важной частью современных ракетных двигателей и сверхзвуковых реактивных авиационных двигателей.

Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами. Эффективные сопла современных ракетных двигателей профилируются на основании газодинамических расчётов.

Существующие методика расчётов дают достаточно точный результат, но требуют больших затрат времени и сил. Авторами сделана попытка смоделировать некоторые ключевые зависимости.

В качестве инструмента моделирования применен корреляционно-регрессионный анализ. Исследования основывались на данных, полученных по известным методикам.

В отличие от функциональной, корреляционная зависимость не является строго определенной, так как кроме исследуемого параметра, на функцию влияют и другие факторы. Тем не менее, общая закономерность изменения функции прослеживается четко, хотя и не строго.

В зависимости от количества рассматриваемых факторов корреляционно-регрессионный анализ подразделяется на парный и многофакторный.

Парный корреляционно-регрессионный анализ устанавливает связь между двумя (парой) факторами, многофакторный – между n факторами. Парные зависимости подразделяются на линейные и нелинейные.

Неизвестные параметры рассчитываются по методу наименьших квадратов, сущность которого состоит в том, что сумма квадратов отклонений расчетных значений от фактических есть величина минимальная.

Теснота криволинейной связи определяется по корреляционному отношению

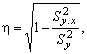где ,

Чем ближе h к единице, тем теснее криволинейная связь между исследуемыми случайными величинами. Если h = 0, то между y и x корреляционная связь отсутствует.

Для проверки согласованности полученных зависимостей с данными эксперимента используется статистика Стьюдента t. Для этого вычисляем значение t: и сравниваем его с табличным значением .

Если вычисленное значение где – табличное значение статистики Стьюдента, то корреляционная связь между рассматриваемыми y и x отсутствует. В противном случае полученная модель является согласованной с данными эксперимента и может быть рекомендована для практического применения.

Согласованность построенной зависимости с данными эксперимента можно осуществлять и по критерию Фишера:

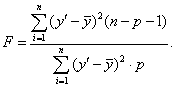
С помощью данного критерия проверяется гипотеза H₀: .

Если где – критическое значение распределения Фишера, соответствующее уровню значимости a, порядку p и числу степеней свободы , то нулевая гипотеза H₀: отвергается, т.е. считается, что построенная парабола порядка P согласуется с данными эксперимента. В противном случае считается, что парабола не согласуется с данными эксперимента.