Лебедев Е.П., Веренич И.А.

Белорусский национальный технический университет, г. Минск

МНОГОФАКТОРНОЕ МОДЕЛИРОВАНИЕ В РАСЧЁТЕ СОПЛА ЛАВАЛЯ

Каналы с суживающейся входной и расширяющейся выходной частью широко применяются в технике. Если они предназначены для преобразования дозвукового потока в сверхзвуковой, то называются соплами Лаваля. Заставив газ протекать под действием достаточно большого перепада давлений сначала через суживающийся, а затем через расширяющийся канал, можно осуществить течение с непрерывно возрастающей скоростью и достигнуть на выходе из сопла скорости истечения большей скорости звука в этом же выходном сечении.

Различают два типа нерасчетного режима. При первом из них струя газа в том месте, где давление газа становится равным внешнему давлению P_вн, отрывается от стенок сопла и выходит в виде цилиндрической струи. При втором режиме, который наблюдается в соплах с небольшим углом раствора расширяющейся части (10-12°), струя не отрывается от стенок сопла. Все эти режимы течения имеют только теоретическое значение, так как в действительных соплах всегда имеется трение, а также скачки уплотнения (в сверхзвуковой части сопла), которые нарушают изоэнтропический характер течения.

Существующие методика расчётов дают достаточно точный результат, но требуют больших затрат времени и сил. Авторами сделана попытка смоделировать некоторые ключевые зависимости с помощью многофакторного корреляционно-регрессионного анализа.

Многофакторный корреляционно-регрессионный анализ используется для установления одновременной зависимости между y и n факторами x1, …, xn, влияющими на исследуемую случайную величину y.

Создание многофакторных моделей требует конкретизации включаемых в модель факторов. Поэтому корреляционно-регрессионному анализу предшествует всесторонний теоретический анализ возможности существования связи между исследуемыми явлениями – факторный анализ.

Теснота связей между y и исследуемыми факторами , оценивается с помощью коэффициента множественной корреляции:

,

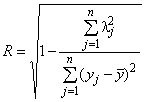где ; – фактические данные; .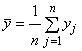

Согласованность полученных моделей с данными эксперимента проверяется по F-критерию: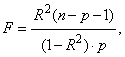

где p – число независимых переменных x_i.

Вычисленное значение F сравнивается с табличным , где v₁= p и v₂= n – p –1; a – принятый уровень значимости. Если вычисленное значение – модель согласуется с фактическими данными. Если вычисленное значение – модель не согласуется с фактическими данными.

Авторами были построены многофакторные модели для ряда факторов.

Уравнение регрессии для всей длинны сопла:

_,

_{Где d-диаметр входного сечения (м), М-число Маха, P-давление (МПа).}

_{Коэффициент множественной корреляции R=0.969. Критерий Фишера F=26.}

_{Для сверхзвуковой части сопла}

Где d_кр-критический диаметр сопла (м), l-длинна сверхзвуковой части сопла.

_{Коэффициент множественной корреляции R=0.921. Критерий Фишера F=5,9.}

Полученные модели имеют высокий коэффициент множественной корреляции и хорошо согласовываются с данными эксперимента. Модели могут быть рекомендованы для практического использования при соответствующих исследованиях.

Литература

1. Вентцель Е.С. Исследование операций. М.:Сов. радио, 1972,-400с.

2. Монахов В.М. Методы оптимезации. М.:Просвещение, 1978,-342с.