Технічні науки / 3. галузеве машинобудування                                                                   

Гордєєв 0.А.,   Крмаліта А.К.

Хмельницький національний університет

 

ПОБУДОВА АНАЛІТИЧНОЇ МОДЕЛІ РУХУ РІДИНИ У СФЕРИЧНІЙ ЛУНЦІ

 

Значна частина витрат на обслуговування і ремонт обладнання легкої промисловості, а саме різноманітних швидкісних швейних машин,  пов'язано зі зношуванням вузлів тертя. У той час при пусках і зупинках  має місце найбільший знос. Однією з головних причин непропорційно великого зносу під час пуску є те, що режим змащування вузлів тертя при цьому принципово відрізняється від режиму змащування вузлів при нормальних обертах двигуна. Чим надійніше утримується мастильний матеріал між контактуючими деталями, тим менше вони зношуються. Зменшення пускового зносу можливе, головним чином, за рахунок поліпшення умов змащування в пусковий період.

Утримання масляного шару в з’єднанні на довгий період роботи є актуальною задачею.

Одним з ефективних і простих способів підведення мастильного матеріалу в зону фрикційного контакту і його тривалого утримування там є створення на контактуючих поверхнях спеціального профілю, що складається із сукупності мікроканавок. Форма і розміри канавок визначаються технологією їх отримання [1, 2].

Найбільше розповсюдження отримали методи нанесення мастилоутримувальних профілів за допомогою вібронакочування. При цьому наноситься система поперечних синусоїдальних канавок за рахунок обертання заготовки, поздовжньої подачі (в основному на токарних верстатах) і додаткових коливань інструменту.

На теперішній час нанесення мастилоутримувального рельєфу у вигляді лунок на шийку вала пропонується наносити дискретним гідроструминним способом за допомогою вібраційної машини [3, 4, 5].

 

Метою даної  роботи є побудова аналітичної моделі руху мастила у мастилоутримувальних  сферичних лунках для визначення величини рівня  мастильного шару, коли виконується умова мастилоутримання та картини руху мастила у сферичних мастилоутримувальних лунках на шийці валу.

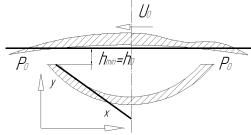
Представимо рух мастилоутримувальної канавки на шийки валу в підшипнику ковзання у вигляді задачі плоского руху в’язкої рідини між  непаралельними площинами.  Для зручності побудови аналітичної моделі приймемо наступне: залишивши незмінним відносний рух поверхонь приймемо, що рухається поверхня підшипника з швидкістю U0  у напрямку від’ємної осі Х, нижня поверхня нерухома (рис. 1), мінімальну товщину мастильного шару приймемо:  hmin .

Рис. 1 – Схема руху поверхонь з елементами апроксимації

Простір зліва і справа будемо рахувати заповненим в’язкою рідиною, яка знаходиться під однаковим тиском Р0. Оскільки рух розглядається у площини то Uz = 0. Розподіл швидкостей у шарі в’язкої рідини описується рівнянням:

 

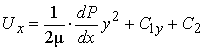.                                       (1)

Для визначення граничних меж знайдемо з геометричних умов залежність  . З метою спрощення опису ліву  частину  поверхні лунки рахуємо прямолінійною. Тоді можна записати:

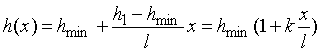,                       (2)

        де параметр 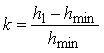 -  параметр шару.

Граничні умови запишемо наступним чином:

   як що     як що              (3)

                          як що   та    або   і          

Визначивши при цих граничних умовах постійні С1 і С2  отримаємо закон розподілу повздовжньої швидкості:

                                       (4)

Для отримання залежності, яка визначає розподіл тиску в шарі , врахуємо, що  у відповідності з рівнянням нерозривності маємо:

.

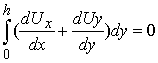Оскільки;

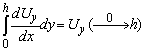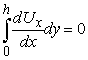, та з урахуванням граничних умов для  зробимо висновок, що:                   або      .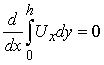

Застосувавши вираз (11) та виконав інтегрування отримаємо:

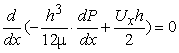     .                                                  (5)

Оскільки вираз у дужках не залежить від x  та  y то його прирівнюємо до постійної, яку приймаємо наступним чином:

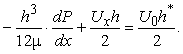
Це рівняння можливо перезаписати наступним чином:

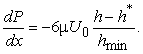                                            (6)

Постійна    має значення товщини шару мастила при якій , тобто коли тиск досягає максимального значення.  Врахуємо, що  тоді згідно рівняння (2) отримаємо:

                                                     (7)

Тоді замість рівняння (5) маємо:

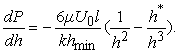                                       (8)

Провівши інтегрування отримаємо:

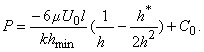
Використовуючи граничні умови (3) та перетворення отримаємо:

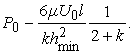  =                              (9)

Остаточно рівняння розподілу тиску по довжині шару приймає вигляд:

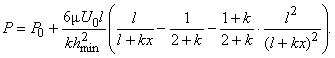
З рівняння розподілу швидкостей (4) видно, що на дільниці , де , можливе таке співвідношення параметрів при якому . Це говорить, що рух проходить в сторону, протилежну швидкості  U0, тобто виникає зворотний рух рідини. Виникнення зворотної течії супроводжується відривом основного потоку від поверхні і пояснюється дією зворотного перепаду тиску. Розглянемо умови відриву потоку:

.

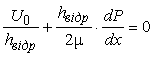З урахуванням того що: 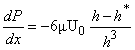  ,  знаходимо:

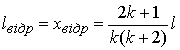    або     .                           (10)

Звідси можна зробити  висновки, якщо      та    ,     то при цих

значеннях течія по довжині лунки буде безвідривна і умова мастилоутримання не буде виконана.

Якщо  відрив здійснюється у точці  (рис. 2).

Тоді рух змащувального шару у сферичній лунці набуде вигляду рис. 3. 

 

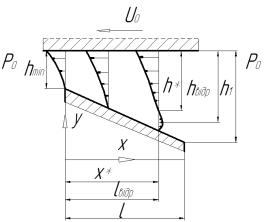
Рис. 2 – Розрахункова схема течії змащувального шару

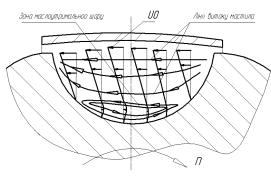
Рис. 3 – Схема руху течії змащувального шару у лунці

Було проведено аналіз впливу геометричних параметрів лунки, а саме параметру шару  та на глибину . Скористуємося залежностями (9) і (10) та отримаємо:

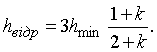                                              (11)

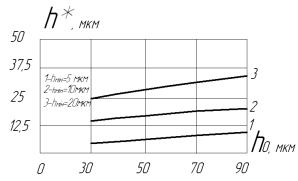
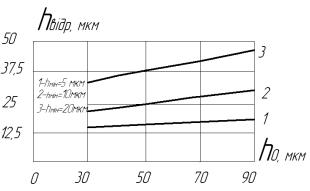
Задавшись межами зміни   від 5 мкм до 20 мкм, а зміну меж   від 30 мкм до 90 мкм та скориставшись залежністю (22) побудовано графіки залежностей та  від цих параметрів (рис. 4, рис. 5).

 

 

 

Рис. 4 – Залежність глибини несущого шару від глибини лунки

Рис. 5 – Залежність глибини несущого шару від глибини лунки

 

Висновки

1. У результаті проведених досліджень встановлено параметри виникнення зворотного руху рідини у лунці та показано виникнення кругового руху у мастилоутримувальному шарі рідини, що говорить про виконання умов утримання мастила у лунці на величині .

2. Отримані залежності глибини  і  несущого шару від розмірів лунки показали значний вплив  на товщину змащувального шару та більш менший вплив на нього глибини лунки .

 

Література

1. Шнейдер Ю. Г. Эксплуатационные свойства деталей с регулярным микрорельефом / Ю. Г. Шнейдер. − Л.: Машиностроение, Ленингр. отд-ние, 1982. − 248 с.: ил.

2. Одинцов Л. Г. Финишная обработка деталей алмазным выглаживанием и вибровыглаживанием / Л. Г. Одинцов. − М.: Машиностроение, 1981. − 160 с.

3. Гордєєв О.А. Технологія та вібраційне обладнання для нанесення маслоутримуючих лунок на поверхні ковзання / О.А. Гордєєв., А.К. Кармаліта // Materiali VIII miedzynarodowej naucowi-practicznej konferencji «NAUKA I INOWACJA – 2012» 07-15 pazdziernika 2012 roku. Volume 21 Techniczne nauki. / Przemysl. Nauka I studia. 2012. С 9 − 11.

   4. Гордєєв Олексій. Вібраційне обладнання для нанесення мастилоутримуючих лунок / О. Гордєєв, А. Кармаліта  // МСУИЛМ-11 : тези доповідей. – Львів,  2013. – С. 65 − 66.

   5. Пат. на корисну модель 81625 України, МПК В24C 1/00. Вібраційний пристрій для нанесення масло утримуючих лунок на шийках валів / М.Є. Скиба, А.К. Кармаліта, О.А. Гордєєв (Україна); заявник і патентовласник Хмельницький нац. ун-т.– u 201214215; Заяв. 13.12.2012; Опубл. 10.07.2013,  Бюл. № 13. – 3 с.