Гурвич Ю.А., Лебедев Е.П.

Белорусский национальный технический университет, Минск

Формализация задачи определения динамических характеристик шин

В качестве критерия оптимальности, устанавливающего меру близости между совокупностью расчетных частотных характеристик уравнений неголономных связей и соответствующей совокупностью экспериментальных частотных характеристик, может быть использована одна из двух наиболее употребительных на практике норм Чебышева или Гильберта

(1)

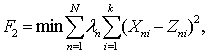(2)

где λ_n – весовые коэффициенты.

Статистический анализ целевых функций (1), (2) и данных экспериментов, которые:

-соответствуют вероятностной модели;

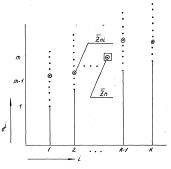
- разбиты на i групп по j измерений в каждой группе (рис. 1); - зависят от одного фактора - дискретных значений путевой частоты ω_i, показал, что в качестве весовых коэффициентов необходимо использовать отношение

(3)

где - дисперсия однофакторного дисперсионного анализа, представляющая сумму межгрупповой (i) и внутригрупповой (j)дисперсии

- среднее измерений в i-той группе;

- среднее всех измерений (рис. 1).

Рис.1. Соответствие экспериментальных данных предпосылкам вероятностной модели: -число групп; - число измерений в группе

Обобщённый критерий представляет собой совокупность четырех разнородных частотных характеристик и формируется с помощью весовых коэффициентов (3), имеющих размерность дисперсии, на основе нормы Гильберта (2)

(4)

Совокупность параметрических ограничений и целевой функции представляет собой математическую модель идентификации процесса качения колеса.

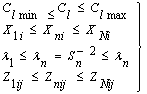
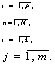(5)

_______________

F₃ → min.

Анализ частотных характеристик уравнений связей в случае боковых и угловых колебаний колеса и сопоставление их с результатами различных экспериментов с шиной позволяют утверждать, что пригодными для идентификации в диапазоне путевой частоты от 0 до 25 рад/м оказались четыре частотные характеристики, полученные при боковых колебаниях:

(6), (7)

(8),(9)

где - амплитудные частотные и фазовые частотные характеристики боковой силы и стабилизирующего момента в функции дискретных i-тыx значений путевой частоты; j₁ -мнимая единица.

Анализ частотных характеристик (6) и (9) уравнений связей показал, что число оцениваемых коэффициентов может колебаться от двух (С₁ и С₂), если использовать совокупность фазовых частотных характеристик (7) и (9) или какую-либо одну из них, до четырех в случае учета совокупности частотных характеристик (6) и (8) или (6)-(9). При этом информативность целевой функции, которая зависит от количества C_l, от числа и вида используемых X_ni является переменной. Указанное обстоятельство приводит к необходимости установления иерархии среди целевых функций (а также среди механико-математических моделей), исходя из их информативности.

В результате анализа установлено, что наибольшей информативностью обладает модель, содержащая все четыре амплитудные и фазовые частотные характеристики, которая позволяет одновременно оценивать четыре коэффициента шин.

ЛИТЕРАТУРА

1. Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. — М.: Наука, 1967.— 519 с.

2. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования.— М.: Наука, 1975.— 767 с.