Технические науки / 4. Транспорт

К.т.н. П.В. Харламов

федеральное государственное бюджетное учреждение высшего профессионального образования «Ростовский государственный университет путей сообщения», Россия, г. Ростов-на-Дону,

ПРИМЕНЕНИЕ МЕТОДА ФИЗИКО – МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ ФРИКЦИОННОГО КОНТАКТА НА ПРИМЕРЕ ДИСКОВОГО ТОРМОЗНОГО МЕХАНИЗМА АВТОМОБИЛЯ

Узел трения «тормозной диск – колодка» является составной частью фрикционно-механической системы «автомобиль – дорожное покрытие». Тормозной диск и тормозная колодка совершают взаимное перемещение, при этом сопряженные поверхности представляют подсистему низшего уровня, составными частями которой являются микронеровности, которые принято характеризовать массой их активного микрообъема и жесткостью заделки [1, 2].

При выполнении физико-математического моделирования фрикционного контакта диско-колодочного тормоза автомобиля необходимо учитывать структуру фрикционной механической системы «автомобиль – дорожное покрытие» (рисунок). Это позволит учесть взаимное влияние фрикционных подсистем, рассматриваемой механической системы, для обеспечения динамического подобия натурного и модельного фрикционных контактов.

Данная работа выполнена при поддержке грантов Президента РФ (МК-2013) гос. контракт МК-7139.2013.8.

Подсистема механической части узла трения характеризуется: параметрами режима (скорость, нагрузка), теплоотдающими поверхностями и объёмами теплопоглощения, а также параметрами формы (масса, жёсткость, моменты инерции, твёрдость, и т.д.). Фрикционная подсистема низшего уровня определяется параметрами микрогеометрии контакта (высота и радиус активного микрообъёма, величина сближения контактирующих поверхностей), средней объёмной и максимальной температурами фрикционного контакта, градиентом температуры, напряженно-деформационным состоянием активных микрообъемов [1, 2].

Для обеспечения идентичности видов процессов изнашивания при модельных и натурных испытаниях фрикционных механических систем необходимо обеспечить [1, 3, 4]:

- идентичность динамических характеристик всех подсистем натуры и модели;

- идентичность процессов трения, изнашивания и физико-механических характеристик контактирующих поверхностей, а также третьего тела;

- идентичность термодинамических процессов протекающих на фрикционном контакте;

- учет взаимовлияния динамических процессов протекающих на фрикционных контактах в механической системе при модельных и натурных испытаниях.

По условиям эксперимента данные положения могут быть выполнены только при обеспечении равенству единицы константы подобия: времени, амплитуды деформаций микронеровностей, контактного давления, параметра PV.

В системе основных единиц MLTQ (масса, длина, время и температура) выбираем четыре базисных параметра, оказывающих наиболее существенное влияние на процессы трения и изнашивания фрикционной системы [4]:

1. Коэффициент теплоотдачи s /s/ = /M¹ L⁰ T^-3 Q^-1/;

2. Нормальная нагрузка на тормозную колодку N /N/ = /M¹ L¹ T^-2 Q⁰/.

3. Скорость скольжения V /V/ = /M⁰ L¹ T^-1 Q⁰/;

4. Геометрический масштаб l, м /l/ = /M⁰ L¹ T⁰ Q⁰/.

Система уравнений, образованная четырьмя базисными параметрами имеет вид [1, 2]:

lns = lnM + 0×lnL – 3×lnT – lnQ;

lnN = lnM + lnL –2×lnT + 0×lnQ; (1)

lnV = 0×lnM + lnL – lnT + 0×lnQ;

ln l = 0×lnM + lnL + 0×lnT + 0×lnQ.

Главный определитель D₀ системы уравнений в числовой форме, образованный параметрами MLTQ:

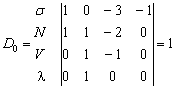. (2)

Определитель (2) подтверждает независимость выбранных базисных параметров.

На этапе проведения лабораторного эксперимента, необходимо учесть ряд ограничений, определяющих механическое, тепловое и динамическое подобие всей механической системы для реализации аналогичных физических процессов на фрикционном контакте модели и объекта. Для этого при использовании метода анализа размерностей частота колебаний k, контактное давление q и градиент температуры DQ вводятся в краевые условия [5, 6], то есть С_k=1, С_q=1, C_DQ=1.

Для проведения модельного эксперимента фрикционного контакта с учетом данных [1, 2, 3, 4, 7] зависимость коэффициента трения можно представить в виде:

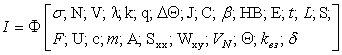, (3)

где J – момент инерции; С – жёсткость круговая; b – вязкое демпфирование; HB – твёрдость материалов; Е – модуль упругости; t – время трения; L – путь трения; S – номинальная площадь фрикционного контакта; F – сила трения; U – весовой износ; c – коэффициент удельной теплоёмкости; m – масса; А – амплитуда деформации связей; S_xx – спектральная плотность мощности амплитудного сигнала силы трения, приходящаяся на единицу площади касания; W_xy – комплексный коэффициент передачи двух сигналов; V_N – скорость нарастания нагрузки; d – сопротивление плёнок окислов срезу, Q – температура вспышки, k_вз – коэффициент взаимного перекрытия

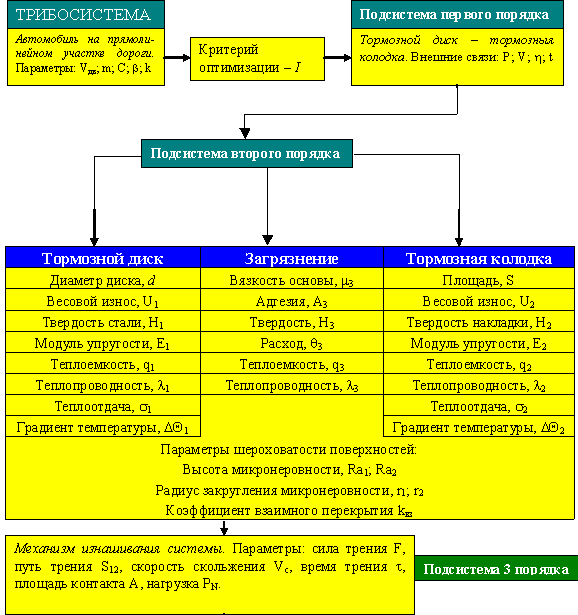
Иерархическая структура фрикционной системы «автомобиль – дорожное покрытие»

Используя главный определитель системы D₀, объединим каждый параметр с базисными s, N, V, l. Для этого поочерёдно заменяем строки с параметрами s, N, V, l строками с размерностями параметра, для которого определяется критерий подобия. Для каждого параметра получим четыре определителя, после чего выведем критерии подобия.

Критерий градиента температуры [DQ] = [M⁰ L^-1 T⁰ Q¹].

Расчёт определителей:

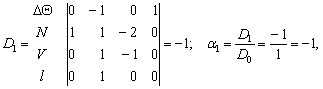
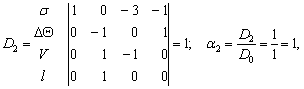
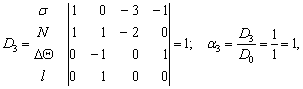
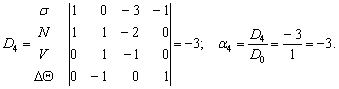
Критерий подобия для параметра градиента температуры DQ будет иметь вид:

или , (4)

тогда .

Проверка: .

Критерий амплитуды деформации связей [A]=[M⁰ L¹ T⁰ Q⁰].

Расчёт определителей:

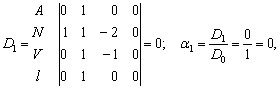
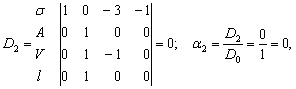
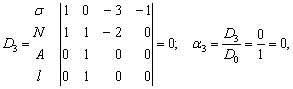
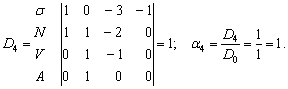
Критерий подобия для параметра амплитуды деформации связей A будет иметь вид:

или , (5)

тогда .

Проверка: , что подтверждает неизменяемость микрогеометрии поверхностей при модельных и натурных исследованиях. Аналогичным образом выражаются через базисные параметрами все остальные параметры процесса трения, принятые для моделирования. Результаты расчета масштабных коэффициентов перехода, характерных для фрикционного контакта «тормозной диск – тормозные колодки» представлены в таблице.

Результаты расчета масштабных коэффициентов перехода для модели узла трения

Параметр	Размерность в системе СИ	Критерий подобия, = idem	Масштабный коэффициент перехода	Формула пересчёта с оригинала на модель
1	2	3	4	5
Коэффициент теплоотдачи, s	Вт/(м^2×^°К)	Базисный параметр
Нормальная нагрузка на тормозную колодку, N	Н	Базисный параметр
Скорость скольжения, V	м/с	Базисный параметр
Линейный размер, l	м	Базисный параметр	– задается
Частота колебаний, k	Гц
Контактное давление, q	Па
Градиент температуры, DQ	^°К/м
Момент инерции, J	кг×м^2
1	2	3	4	5
Демпфирование, b	Н×с/м
Твёрдость, HB	Па
Модуль упругости, Е	Па
Время трения, t	C
Путь трения, L	М
Номинальная площадь фрикционного контакта, S	м^2
Сила трения, F	Н
Весовой износ, U	кг/м^3
Теплоёмкость, c	Дж/^°К
Спектральная плотность мощности сигнала на единицу фактической площади касания, Sxx	Н^2/(м^2×Гц)
Жёсткость круговая, С	Н×м/рад
Масса, m	Кг
Амплитуда деформации связей, А	М
Комплексный коэффициент передачи фрикционной системы, Wxy	—
Скорость нарастания нагрузки, VN	Н/с
Температура тормозного диска, Q	°К
Коэффициент взаимного перекрытия, kвз	—
Сопротивление плёнок срезу, d	Па

Уравнение подобия, объединившее полученные критерии, состоит из 22 критериев, так как согласно теореме Бэкингэма должно быть равно числу параметров за вычетом четырех базисных:

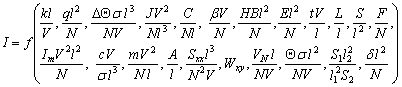. (6)

Критерии подобия, представленные в таблице 1 получены как зависимость моделируемой величины от базисных параметров. Для проверки правильности их определения составим «стандартные» критерии подобия:

1. Критерий гомохронности, характеризующий однородность процессов во времени: , получается, если критерий времени p_t разделить на критерий пути трения p_L, то есть, . Так как в выражение критерия гомохронности входят параметры V, t, L, то даже если ни один из этих параметров не входит в число базисных, перемножение критериев скорости и времени и деление на критерий пути в результате обеспечивает получение критерия гомохронности.

2. Критерий Ньютона, характеризующий отношение удельной нагрузки к удвоенной плотности энергии, получим, если критерий силы трения p_F умножим на критерий времени p_t, разделим на критерий массы p_m и подставим значение , то есть .

3. Критерий Фруда, характеризующий относительную величину силы тяжести, получим, если критерий массы p_m разделим на критерий времени p_t с последующей подстановкой N = mg и : , умножив на квадрат критерия гомохронности, получаем .

4. Критерий Био, характеризующий отношение перепада температуры по толщине пластины к разности температур пластины и среды, можно получить, если критерий градиента температуры p_DQ разделить на критерии разности температур p_Q и линейных размеров p_l .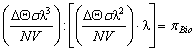

5. Критерий Нуссельта, характеризующий коэффициент теплоотдачи для жидкостных материалов, можно получить, если критерий пути p_L разделить на критерий теплопроводности p_l: .

6. Критерий Фурье, характеризующий для нестационарных процессов соответствие между средней скоростью изменения условий в окружающей среде и средней скоростью перестройки температурного поля внутри тела, получим, если критерий температуропроводности p_Ql разделим на критерий пути трения p_L с последующей подстановкой : .

Для учета взаимного влияния фрикционных подсистем рассматриваемой механической системы необходимо выполнение дополнительно выведенных критериев, однозначно характеризующих исследуемые триботехнические процессы:

1. Критерий идентичности реализации тормозного усилия, характеризующий постоянную величину тормозного усилия, если критерий номинальной площади фрикционного контакта p_S умножить на критерий сопротивления плёнок загрязнений срезу p_d и разделить на критерии скорости нарастания нагрузки p_Vn и коэффициента взаимного перекрытия p_Kвз с последующей подстановкой :

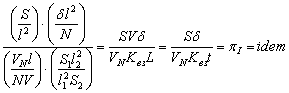, (7)

2. Критерий идентичности тормозного пути, если критерий тормозного пути трения p_L разделить на произведение критериев площади пятна контакта шины p_Sш, давления воздуха в шине p_P и времени торможения p_t с последующей подстановкой :

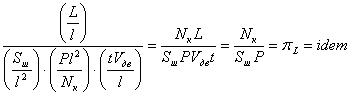, (8)

где N_к – нормальная нагрузка на колесо; V_дв – линейная скорость автомобиля.

3. Критерий идентичности охлаждения тормозного механизма, если критерий температуры тормозного диска p_Q умножить на критерий площади тормозного диска, обдуваемого воздушным потоком p_S.

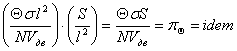, (9)

Таким образом, приведенные выражения позволяют определить критерии подобия перехода от объекта исследования к модельному эксперименту, выполнить стендовые испытания и перенести результаты испытаний на объект исследования.

На основании выше изложенного можно сделать следующие выводы:

1. Установлено, что для физико-математического моделирования фрикционного контакта диско-колодочного тормоза автомобиля необходимо использование в качестве базисного параметра коэффициента теплоотдачи.

2. Разработана иерархическая структура фрикционной механической системы «автомобиль – дорожное покрытие», устанавливающая взаимосвязь двух подсистем «колесо-покрытие дороги» и «диск - колодка».

3. Для учета взаимного влияния фрикционных подсистем (см. рисунок) системы «автомобиль – дорожное покрытие» при моделировании необходимо использование дополнительных критериальных соотношений:

Литература

1. Шаповалов В.В. Комплексное моделирование динамически нагруженных узлов трения машин. Трение и износ.-1985. №3, с.451-457.

2. Щербак П.Н. Оптимизация фрикционных механических систем на базе модельного эксперимента // Щербак Петр Николаевич автореф. дис. на соискание степени доктора технических наук, Ростов-на-Дону, 2002 г. 46с.

3. Заковоротный В.Л., Шаповалов В.В. Исследование комплексного коэффициента трения. // Трение и износ. 1987, с. 22-24.

4. Патент РФ, МПК G 01 N 3/56. Способ испытаний узлов трения / В.В. Шаповалов, А.Л. Озябкин, П.В. Харламов [и др.]. – № 2343450; заявл. 10.01.2009; приоритет 24.04.2008, № 2006121024/28 (022825).

5. Заковоротный В.Л. Динамика трибосистем. Самоорганизация, эволюция. Ростов н/Д: ДГТУ, 2003.-501 с.

6. Заковоротный В.Л., Блохин В.П., Алексейчик М.И. Введение в динамику трибосистем. Ростов н/Д: ИнфоСервис, 2004.-680 с.

7. Заковоротный В.Л., Шаповалов В.В. Исследование коэффициента трения при периодических движениях. // Известия Северо-Кавказского научного центра высшей школы. Сер. Технических наук, 1979, №2, с. 40-49.