Лебедев В.А.
СО РАН Институт теплофизики им. С.С. Кутателадзе, Новосибирск, Россия
ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА ИЗЛУЧАЮЩИХ
СИСТЕМ, СОДЕРЖАЩИХ ОСЕСИММЕТРИЧНЫЕ ЭЛЕМЕНТЫ
Предлагаются графический метод эквивалентных площадей для
вычисления интегральных угловых коэффициентов излучения при наличии
поверхностей произвольной конфигурации и общая для системы гелиостатов аналитическая
форма взаимосвязи геометрических, координатных и азимутальных параметров.
В работе используются графические и
математические методы и приемы исследования предложенные в [1, 3 - 13] с целью
применения их в решении практических задач, связанных с теплообменом
излучением.
При анализе работы излучающих систем,
необходимо оперировать угловыми коэффициентами излучения (УКИ) ![]() – отношениями
количества лучистой энергии
– отношениями
количества лучистой энергии ![]() , испускаемой излучающими поверхностями
, испускаемой излучающими поверхностями ![]() к количеству энергии
к количеству энергии ![]() , попавшей на облучаемую поверхность
, попавшей на облучаемую поверхность ![]() . Из экспериментальных методов получения УКИ наиболее
доступными и свободными от больших экспериментальных погрешностей являются
методы графические. Прежде, чем рассматривать предлагаемый метод, заметим
следующее. Поскольку УКИ определяет п-ную долю от испущенного излучения с
поверхности i , попавшую
на облучаемый объект k, (
. Из экспериментальных методов получения УКИ наиболее
доступными и свободными от больших экспериментальных погрешностей являются
методы графические. Прежде, чем рассматривать предлагаемый метод, заметим
следующее. Поскольку УКИ определяет п-ную долю от испущенного излучения с
поверхности i , попавшую
на облучаемый объект k, (![]() =
=![]() ), то, считая
испущенную энергию
), то, считая
испущенную энергию ![]() численно
пропорциональной площади
численно
пропорциональной площади ![]() , можно построить условную поверхность с площадью
, можно построить условную поверхность с площадью ![]() =
=![]()
![]() , пропорциональную
, пропорциональную ![]() . Тогда справедливо соотношение
. Тогда справедливо соотношение
![]() =
= ![]() /
/![]() =
= ![]() /
/![]() =
= ![]() .
.
Если форма поверхностей излучающей системы не содержит перегибов или резких изменений радиуса кривизны, то для построения поверхностей с
 площадями
площадями ![]() и
и ![]() можно ограничиться
построением относительно малого числа вспомогательных точек. В качестве
тестового примера приведем определение УКИ
для излучения с плоского круга
можно ограничиться
построением относительно малого числа вспомогательных точек. В качестве
тестового примера приведем определение УКИ
для излучения с плоского круга ![]() на соосную сферу
на соосную сферу ![]() . Поскольку такой УКИ известен в справочной литературе,
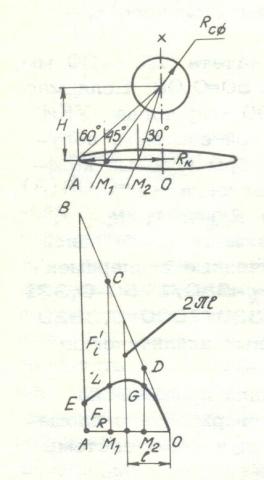
результаты построений легко проверить. Положим радиус
. Поскольку такой УКИ известен в справочной литературе,
результаты построений легко проверить. Положим радиус ![]() = 1, расстояние от центра сферы до центра круга Н = 2, радиус излучающего круга
= 1, расстояние от центра сферы до центра круга Н = 2, радиус излучающего круга ![]() = 2
= 2![]() , рис.1. Строим поверхность,
эквивалентную излучающей поверхности круга с площадью
, рис.1. Строим поверхность,
эквивалентную излучающей поверхности круга с площадью ![]() : с точки А
: с точки А![]() на граничной окружности радиуса
на граничной окружности радиуса ![]() восстанавливаем
перпендикуляр АВ длиной 2
восстанавливаем
перпендикуляр АВ длиной 2![]() и вершину В
перпендикуляра соединяем прямой ВО с
противоположным концом радиуса
и вершину В
перпендикуляра соединяем прямой ВО с
противоположным концом радиуса ![]() (центром круга).
Площадь поверхности
(центром круга).
Площадь поверхности ![]() треугольника АВО равна площади излучающего круга
треугольника АВО равна площади излучающего круга ![]() =
=![]() . Перпендикуляр из любой точки на прямой АО, проведенный до пересечения с ОВ, равен 2
. Перпендикуляр из любой точки на прямой АО, проведенный до пересечения с ОВ, равен 2![]() , где l – расстояние от центра круга О до основания выбранного перпендикуляра. Такой перпендикуляр есть
развернутая на плоскость окружность с радиусом l (AO ≤ l ≤ O), а площадь АВО
– условная излучающая площадь
, где l – расстояние от центра круга О до основания выбранного перпендикуляра. Такой перпендикуляр есть
развернутая на плоскость окружность с радиусом l (AO ≤ l ≤ O), а площадь АВО
– условная излучающая площадь ![]() , эквивалентная площади круга
, эквивалентная площади круга ![]() . Выберем теперь на АО
=
. Выберем теперь на АО
= ![]() точки, с которых
центр облучаемой сферы виден под углами 60˚, 45˚, 30˚, 0˚;
проведем из них перпендикуляры к АО и
определим известным в литературе способом значения локальных УКИ из этих точек (и из
соответствующих им окружностей элементарной ширины длиной АВ, М
точки, с которых
центр облучаемой сферы виден под углами 60˚, 45˚, 30˚, 0˚;
проведем из них перпендикуляры к АО и
определим известным в литературе способом значения локальных УКИ из этих точек (и из
соответствующих им окружностей элементарной ширины длиной АВ, М![]() С, М
С, М![]() D) на поверхности сферы
D) на поверхности сферы ![]() . Численные значения УКИ φ(А,
. Численные значения УКИ φ(А,![]() ), φ(М
), φ(М![]() ,
,![]() ), φ(М
), φ(М![]() ,
,![]() ) изображаем графически в виде отрезков АЕ, М
) изображаем графически в виде отрезков АЕ, М![]() L, М
L, М![]() G на прямых AB, М
G на прямых AB, М![]() C, М
C, М![]() D, соответственно, принимая каждую из этих прямых в
каждом случае равной 1. Отношения длин АЕ/АВ,
М
D, соответственно, принимая каждую из этих прямых в
каждом случае равной 1. Отношения длин АЕ/АВ,
М![]() L/М
L/М![]() G, М
G, М![]() G/М
G/М![]() D численно равны φ(А,
D численно равны φ(А,![]() ), φ(М
), φ(М![]() ,
,![]() ), φ(М
), φ(М![]() ,
,![]() ) соответственно. Перпендикуляр к АО в точке О имеет
нулевую длину, это соответствует тому, что точка О – единственная, не принадлежащая никакому излучающему кольцу,
т.е. не имеет значащей излучающей поверхности, поток энергии с нее – нулевой.
) соответственно. Перпендикуляр к АО в точке О имеет
нулевую длину, это соответствует тому, что точка О – единственная, не принадлежащая никакому излучающему кольцу,
т.е. не имеет значащей излучающей поверхности, поток энергии с нее – нулевой.
Соединив точки E, L, G, O кривой
линией, получаем плоскую фигуру AELGOA с площадью ![]() , численно соответствующей той части всего излучения с
, численно соответствующей той части всего излучения с ![]() =
= ![]() , которая попала на
, которая попала на ![]() . Измерив площади
. Измерив площади ![]() и
и ![]() , из соотношения
, из соотношения ![]() /
/![]() получим значение искомого интегрального УКИ
получим значение искомого интегрального УКИ ![]() .
.
Следует отметить, что меняя масштабы
построений можно менять точность результатов, полученных методом эквивалентных площадей. Например, выбрав ![]() = 35 мм, АВ = 100
мм , получаем
= 35 мм, АВ = 100
мм , получаем ![]() =
= ![]() /
/![]() = 140/1750 = 0.08. Увеличив масштаб вдвое (
= 140/1750 = 0.08. Увеличив масштаб вдвое (![]() = 70 мм, АВ = 200
мм), получаем существенное уточнение:
= 70 мм, АВ = 200
мм), получаем существенное уточнение: ![]() =
=![]() /
/![]() = 583/7000 = 0.08329. УКИ
= 583/7000 = 0.08329. УКИ ![]() для данной системы,
полученный аналитическим методом с помощью алгебры угловых коэффициентов из
известных формул [2], имеет значение
для данной системы,
полученный аналитическим методом с помощью алгебры угловых коэффициентов из
известных формул [2], имеет значение ![]() = 0.08(3).
= 0.08(3).
Методом
эквивалентных (или пропорциональных) площадей можно получить во вполне достаточном для практического применения
приближения значение интегрального УКИ ![]() на осесимметричную
поверхность
на осесимметричную
поверхность ![]() от поверхности
от поверхности ![]() произвольной формы,
принадлежащей соосной с
произвольной формы,
принадлежащей соосной с ![]() осесимметричной
поверхности I или же плоскости II, перпендикулярной оси поверхности
осесимметричной
поверхности I или же плоскости II, перпендикулярной оси поверхности ![]() , рис.2а.
, рис.2а.
Рассмотрим случай, когда поверхность ![]() произвольно
расположена на плоскости II. С помощью
концентрических окружностей с центром О (точка пересечения с плоскостью II оси симметрии поверхности
произвольно
расположена на плоскости II. С помощью
концентрических окружностей с центром О (точка пересечения с плоскостью II оси симметрии поверхности ![]() ) делим площадь
) делим площадь ![]() на такие части,
представляющие собой отрезки плоских концентрических колец, с помощью которых
можно построить описанным выше способом
на такие части,
представляющие собой отрезки плоских концентрических колец, с помощью которых
можно построить описанным выше способом 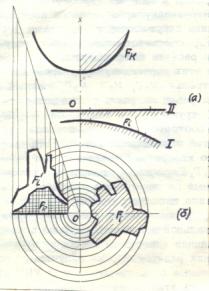 отображение
отображение ![]() поверхности
поверхности ![]() на развертке круга с
соответствующим радиусом, рис.2б. Затем с помощью локальных УКИ (с точек на
построенных окружностях на поверхность
на развертке круга с
соответствующим радиусом, рис.2б. Затем с помощью локальных УКИ (с точек на
построенных окружностях на поверхность ![]() ) строим плоскую фигуру с площадью
) строим плоскую фигуру с площадью ![]() . Следуя приведенным выше соображениям, получаем искомый
интегральный УКИ
. Следуя приведенным выше соображениям, получаем искомый
интегральный УКИ ![]() =
=![]() /
/![]() .
.
Описанный графический метод приводит к
хорошим результатам в случаях неудобных для аналитической обработки из-за
сложности конфигурации поверхности ![]() . Поскольку в практике больший интерес представляют случаи
излучения с
. Поскольку в практике больший интерес представляют случаи
излучения с ![]() на
на ![]() , то для получения УКИ
, то для получения УКИ ![]() следует пользоваться простым соотношением
следует пользоваться простым соотношением ![]() =
=![]()
![]() /
/![]() .
.
Современная вычислительная техника с
использованием графопостроителей существенно облегчает применение предлагаемого
метода эквивалентных площадей
определения интегрального УКИ при наличии поверхностей сложной конфигурации.
 Рассмотрим теперь особенности работы излучающей
системы при наличии облучаемой сферы (накопителя энергии), зеркальных
отражателей (концентраторов) и излучающего шарового (точечного) солнечного источника
излучения – группы гелиостатов на горизонтальной поверхности. В отличие от
гелиостата, рис. (Kreith, 1962), с собственным
накопителем энергии, расположенным на оси параболического зеркала, рассматриваемая
система состоит из ряда зеркальных концентраторов с одним общим накопителем,
находящемся на высоте h над горизонтальной поверхностью. Комплексы таких
систем, составляющих большую промышленную энергетическую станцию, могут
содержать десятки тысяч таких зеркал-гелиостатов. Для облегчения управления ими
следует выделить группы гелиостатов, обладающих общими свойствами.
Рассмотрим теперь особенности работы излучающей
системы при наличии облучаемой сферы (накопителя энергии), зеркальных
отражателей (концентраторов) и излучающего шарового (точечного) солнечного источника
излучения – группы гелиостатов на горизонтальной поверхности. В отличие от
гелиостата, рис. (Kreith, 1962), с собственным
накопителем энергии, расположенным на оси параболического зеркала, рассматриваемая
система состоит из ряда зеркальных концентраторов с одним общим накопителем,
находящемся на высоте h над горизонтальной поверхностью. Комплексы таких
систем, составляющих большую промышленную энергетическую станцию, могут
содержать десятки тысяч таких зеркал-гелиостатов. Для облегчения управления ими
следует выделить группы гелиостатов, обладающих общими свойствами.
 Зенитному расположению Солнца отвечают общие свойства
групп гелиостатов, расположенных концентрически относительно приемника энергии.
Управление гелиостатами в этом случае никаких сложностей не содержит. Интерес
представляет не-зенитное расположение Солнца. Для исследования этого случая
следует ввести систему подвижных координат с началом у основания
перпендикуляра, опущенного из концентратора энергии на горизонтальную
поверхность. Координаты (a,b) этой
системы связаны с неподвижными координатами (x,y) с помощью
угла отклонения β: (a,b) = (x,y)·(cosβ)
Зенитному расположению Солнца отвечают общие свойства
групп гелиостатов, расположенных концентрически относительно приемника энергии.
Управление гелиостатами в этом случае никаких сложностей не содержит. Интерес
представляет не-зенитное расположение Солнца. Для исследования этого случая
следует ввести систему подвижных координат с началом у основания
перпендикуляра, опущенного из концентратора энергии на горизонтальную
поверхность. Координаты (a,b) этой
системы связаны с неподвижными координатами (x,y) с помощью
угла отклонения β: (a,b) = (x,y)·(cosβ)![]() . Если ось Х будет
постоянно ориентирована по Солнцу, то для всех нормалей на ней угол отклонения
Солнца ω от нормали (от
зенитного положения) будет общим у всех гелиостатов каждой из групп, принадлежащих
соответствующим эллиптическим поясам на горизонтальной плоскости. Общая ориентация
гелиостатов определяется общими для их нормалей ориентацией и углом наклона α
. Если ось Х будет
постоянно ориентирована по Солнцу, то для всех нормалей на ней угол отклонения
Солнца ω от нормали (от
зенитного положения) будет общим у всех гелиостатов каждой из групп, принадлежащих
соответствующим эллиптическим поясам на горизонтальной плоскости. Общая ориентация
гелиостатов определяется общими для их нормалей ориентацией и углом наклона α![]() к горизонтальной плоскости. Несложные, но громоздкие
выкладки позволяют получить связь координатных и азимутальных характеристик
гелиостатов с одинаковыми α
к горизонтальной плоскости. Несложные, но громоздкие
выкладки позволяют получить связь координатных и азимутальных характеристик
гелиостатов с одинаковыми α![]() :
:
![]()
= ![]() .
.
Использование этого соотношения освобождает
от необходимости управлять каждым гелиостатом в отдельности, достаточно
оперировать только одним прибором в группе. При этом необходимо знать лишь
положение каждого гелиостата в группе относительно неподвижной системы
координат и переменные значения 1) азимутального положения Солнца и 2) его отклонения от зенита.
Литература
1.
Kreith F.O. Radiation Heat Transfer for Solar Power Plant Design, Scranton,
Pennsylvania, 1962.
2. Зигель Р., Хауэлл Дж. Теплообмен
излучением. М. 1975.
3. Лебедев В.А. Исследование теплообмена и
свойств переноса излучения. Новосибирск. 1979.
4. Лебедев В.А. Радиационный и
комбинированный теплообмен. Новосибирск. 1981.
5. Лебедев В.А. Взаимодействие теплового
излучения с веществом. Новосибирск. 1982.
6.Лебедев В.А. Изв. СО АН СССР. Сер. техн. наук, 1988,
№11-3.
7. Lebedev
V.A. Sov. J. Appl. Phys., vol.2, no.6, 1988.
8. Вардияшвили А.Б., Лебедев В.А., Рубцов
Н.А., Сорокин А.Л. Гелиотехника, 1988, №1.
9. Буланов В.Н. Гелиотехника, 1988, №5.
10. Вардияшвили А.Б., Лебедев В.А.,
Сорокин А.Л. Гелиотехника, 1989, №3.
11. Вардияшвили А.Б., Лебедев В.А.
Гелиотехника, 1989, №4.
12. Рубцов Н.А., Лебедев В.А.
Геометрические инварианты излучения. Новосибирск. 1989.
13. Howell
J.R., Siegel R., Mengüç M.P. Thermal Radiation Heat Transfer.
London, NY, 2011.