Медетбекова Р.А., Шалданбаева А.А.

г. Шымкент, ЮКГУ им. М.Ауезова

ОБ ОДНОМ ПРИЗНАКЕ ОГРАНИЧЕННОСТИ РЕШЕНИЙ УРАВНЕНИЯ ШТУРМА-ЛИУВИЛЛЯ

1. Рассмотрим на полупрямой уравнения Штурма-Лиувилля

, (1.1)

с непрерывным вещественным коэффициентом . Полагая, , , из уравнения (1.1), получим систему уравнений

(1.2)

Известно [4,с.81], что система уравнений (1.2) устойчива по Ляпунову тогда и только тогда, когда ограничены на все ее решения, следовательно, уравнение Штурма-Лиувилля устойчиво по Ляпунову на тогда и только тогда, когда на этой полупрямой ограничены все его решения и их производные. Очевидно, что это слишком ограниченные условия, и в связи с этим возникает следующая задача.

ЗАДАЧА. Если все решения уравнения Штурма-Лиувилля:

,

ограничены на полупрямой , то каким должна быть функция .

Основным результатом статьи является теорема 2.2, вывод которого опирается на теорему 2.1, возможно имеющий и самостоятельное значение.

Отметим, что поставленная задача решена нами (пока) частично, т.е. не в полном объеме, и в следующих работах мы намерены вновь вернуться к этой теме.

2. Рассмотрим на полупрямой уравнения Штурма-Лиувилля с непрерывным вещественным коэффициентом т.е.

, (2.1)

Пусть c и s фундаментальная система решений уравнения (2.1), удовлетворяющий начального условия (2.2):

c, c (2.2)

ОПРЕДЕЛЕНИЕ 2.1. Функций

,, (2.3)

Называем соответственно потенциальной, кинетической полной энергией системы (2.1)+(2.2), а функцию фазой этой системы.

При исследовании задача (2.1)+(2.2) важную роль играют некоторые свойства введенных функций, поэтому сформулируем их в виде леммы, для удобства ссылок.

ЛЕММА 2.1 д)

б) е)

в) ж)

г) з)

ТЕОРЕМА 2.1 (о логарифме). Если вещественная непрерывная функция на полупрямой , то имеет место неравенство:

(2.4)

где , из определения 1.

ДОКАЗАТЕЛЬСТВО. Пусть непрерывно дифференцируемая функция на сегменте , тогда справедливо неравенство:

(2.5)

где . В самом деле, интегрируя по частям левую часть (2.5), имеем:

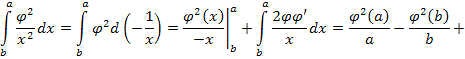
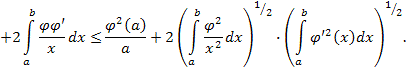
Полагая,

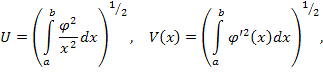
получили квадратное неравенство:

Найдем корни квадратного уравнения:

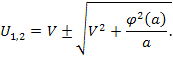
Поскольку , то имеет место неравенство:

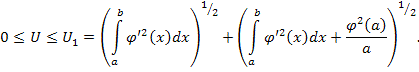
Используя неравенство , получим:

(2.6)

Из постоянства вронскиана уравнения (2.1) имеем:

(2.7)

Разделив вронскиан (2.7) на и проинтегрировав в пределах от 1 до , имеем:

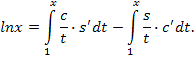
Далее в силу неравенства (2.6), получим:

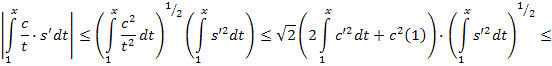
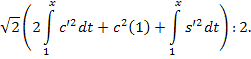
Аналогично, имеем:

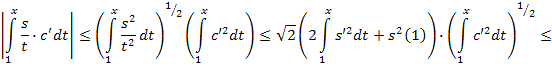
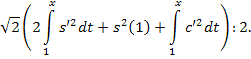
Просуммировав двух последних неравенств, получим:

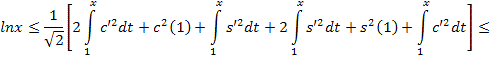
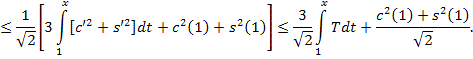
Теорема доказана.

ЛЕММА 2.2 (Абель). Пусть функции и определены в промежутке причем

1) Функция интегрируема в этом промежутке, так что интервал:

(2.8)

сходится (хотя бы и не абсолютно).

2) Функция монотонно и ограничена ,

Тогда интеграл

(2.9)

сходится.

ТЕОРЕМА 2.2. Если при больших , то несобственный интеграл

(2.10)

расходится.

ДОКАЗАТЕЛЬСТВО. Из леммы 1, имеем , интегрируя это равенство, получим:

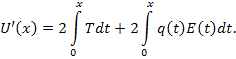
По условию теоремы при , имеем , следовательно:

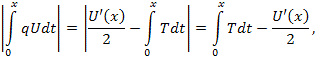
поэтому при , имеет место неравенство:

(2.11)

Из условия (), следует монотонность и ограниченность функции, так что существует постоянная такая, что:

(2.12)

Теперь допустим, что интеграл сходится хотя бы в несобственном смысле (см.(2.8)), тогда в силу леммы Абеля интеграл правой части неравенства (2.11) сходится, а это противоречит к лемме 2 (см.(2.4)). Допущение не верно.

Теорема доказана.

ЛИТЕРАТУРА

1. Шалданбаев А.Ш. \\ Принцип запрета Гамильтона и его применения. – Л. Дел.КазгосИНТИ, 13 июня 1994, № 5074-94. с.29.

2. Гусаров Л.А. Об ограниченности решений линейного уравнения второго порядка. – ДАН СССР, т.18, №2, 1949, с.217-220.

3. Фихтенгольц Г.И. Курс дифференциального и интегрального исчисления, т.2. – М.: Наука, 1970.

4. Демидович Б.П. Лекции по математической теории устойчивости. – М.: Наука, 1967. с.81