Шилинец В.
А., Борис Т. И., Подполухо Е. В.
Белорусский
государственный педагогический университет
МОНОГЕННОСТЬ В СМЫСЛЕ В.С. ФЕДОРОВА И ОБОБЩЕНИЕ БИГАРМОНИЧЕСКИХ ФУНКЦИЙ
Пусть ![]() ,
, ![]() – однозначные функции класса
– однозначные функции класса ![]() для некоторой
односвязной области
для некоторой
односвязной области ![]() плоскости
плоскости ![]() .
.
Через ![]() обозначим
класс действительных или комплексных функций от независимых переменных
обозначим
класс действительных или комплексных функций от независимых переменных ![]() , имеющих в области
, имеющих в области ![]() непрерывные
частные производные до порядка
непрерывные
частные производные до порядка ![]() включительно.
При
включительно.
При ![]() имеем
класс всех непрерывных в области
имеем
класс всех непрерывных в области ![]() функций.
функций.
Полагаем ![]() (
( ![]() ,
, 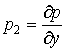 и аналогично для всех
рассматриваемых функций). Будем всегда считать, что в области
и аналогично для всех
рассматриваемых функций). Будем всегда считать, что в области ![]() существует
существует
![]() .
.
При этих условиях формальными производными ![]() и
и ![]() какой-нибудь
функции
какой-нибудь
функции ![]() класса
класса
![]() называются такие
функции от
называются такие
функции от ![]() и
и ![]() , которые в области
, которые в области ![]() определяются
следующим образом [1]:
определяются
следующим образом [1]:
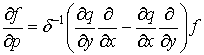 ,
, 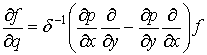 . (1)
. (1)
Далее заметим, что если в области ![]() имеем
имеем
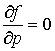 , то это свидетельствует о том, что функция
, то это свидетельствует о том, что функция ![]() является моногенной в
смысле
является моногенной в
смысле
В.С. Федорова (F-моногенной)
относительно функции ![]() в области
в области ![]() [1, 2].
[1, 2].
Пусть ![]() . Тогда можно определить формальные производные второго
порядка
. Тогда можно определить формальные производные второго
порядка 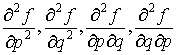 :
:
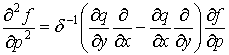 ,
, 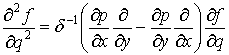 ,
,
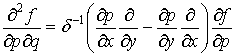 ,
, 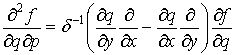 .
.
Отметим, что в области ![]()
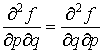 [1].
[1].
В работе [1] В.А. Гусевым было исследовано уравнение ![]() , где
, где 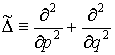 ;
; ![]() – искомая
функция класса
– искомая
функция класса ![]() ;
; ![]() – известные функции
того же класса.
– известные функции
того же класса.
Предметом исследования в данной работе является
дифференциальное уравнение в формальных производных
![]() , (2)
, (2)
где 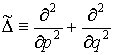 ; показатель 2 свидетельствует о том, что оператор
; показатель 2 свидетельствует о том, что оператор ![]() используется
последовательно два раза, т. е.
используется
последовательно два раза, т. е. ![]() ;
; ![]() – известные
(искомая) функции класса
– известные
(искомая) функции класса ![]() .
.
Рассмотрим бикомплексные функции ![]() ,
, ![]() ,
, ![]() (
(![]() ,
, ![]() ) [3]. Будем использовать
далее следующие обозначения:
) [3]. Будем использовать
далее следующие обозначения: ![]() ,
, ![]() .
.
Тогда
из равенств (1), определяющих формальные производные, имеем
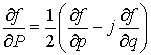 ,
, 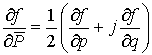 ,
,
откуда следует 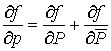 ,
, 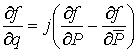 . Поэтому имеем
. Поэтому имеем
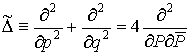 .
.
Таким
образом, уравнение (2) равносильно уравнению
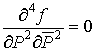 , которое, очевидно, можно записать в следующем виде:
, которое, очевидно, можно записать в следующем виде:
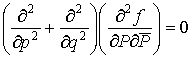 . (3)
. (3)
Проинтегрируем сначала уравнение вида
![]() , (4)
, (4)
где 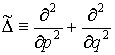 [1].
[1].
Лемма 1. Выражение ![]() будет полным
дифференциалом (по переменным
будет полным
дифференциалом (по переменным ![]() ) в области
) в области ![]() тогда и только тогда,
когда
тогда и только тогда,
когда 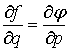 ,
, ![]() .
.
Лемма 2. Пусть ![]() ,
, ![]() ,
, ![]() , (
, (![]() ,
,![]() ). Бикомплексная функция
). Бикомплексная функция ![]() будет моногенной в
смысле В.С. Федорова в области
будет моногенной в
смысле В.С. Федорова в области ![]() по бикомплексной
функции
по бикомплексной
функции ![]() тогда и только тогда,
когда в рассматриваемой области
тогда и только тогда,
когда в рассматриваемой области
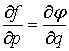 ,
, 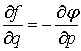 . (5)
. (5)
Теорема 1. Если ![]() – любая бикомплексная
функция, моногенная по бикомплексной функции
– любая бикомплексная
функция, моногенная по бикомплексной функции ![]() в односвязной области
в односвязной области
![]() плоскости
плоскости ![]() , то функция
, то функция ![]() является решением
дифференциального уравнения (4).
является решением
дифференциального уравнения (4).
Перейдем
сейчас к интегрированию дифференциального уравнения в формальных производных
(3).
Полагаем
![]() , (6)
, (6)
тогда
уравнение (3) примет следующий вид:
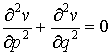 . (7)
. (7)
Используя теорему 1, получаем, что
функция ![]() является решением
уравнения (7), где
является решением
уравнения (7), где ![]() – произвольная
моногенная в смысле В.С. Федорова по функции
– произвольная
моногенная в смысле В.С. Федорова по функции ![]() в области
в области ![]() функция.
функция.
Легко
убедиться в том, что если функция ![]() является
является
F-моногенной по функции ![]() в области
в области ![]() , то в этой области функция
, то в этой области функция ![]() будет F-моногенной по функции
будет F-моногенной по функции ![]() .
.
Таким
образом, решение дифференциального уравнения (7) имеет следующий вид:
![]() ,
(8)
,
(8)
где ![]() – произвольная
моногенная в смысле В.С. Федорова в области
– произвольная
моногенная в смысле В.С. Федорова в области ![]() относительно функции
относительно функции ![]() бикомплексная функция.
бикомплексная функция.
Из
равенств (6) и (8) получаем
![]() . (9)
. (9)
Построим, как и в работе [2], функцию 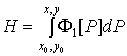
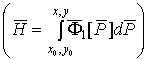 , где
, где ![]() – фиксированная точка
области
– фиксированная точка
области ![]() ,
, ![]() – текущая точка этой
же области. При этом имеем, что
– текущая точка этой
же области. При этом имеем, что ![]() (
(![]() ) – моногенная по функции
) – моногенная по функции ![]() (
(![]() ) в области
) в области ![]() функция,
функция, ![]()
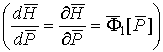 , где
, где ![]()
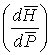 – производная в
смысле В.С. Федорова функции
– производная в
смысле В.С. Федорова функции ![]() по функции
по функции ![]() .
.
Тогда,
на основании равенства (9), получаем
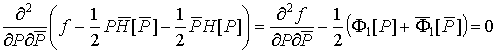 ,
,
откуда
![]()
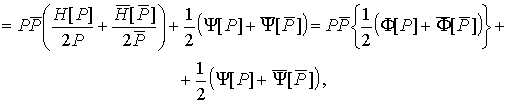
где ![]() ,
, ![]() – бикомплексные
функции, моногенные по бикомплексной функции
– бикомплексные
функции, моногенные по бикомплексной функции ![]() в области
в области ![]() .
.
Из
последнего равенства следует, что ![]() .
.
Таким
образом, получили теорему.
Теорема 2. Решение дифференциального
уравнения в формальных производных (2) имеет следующий вид:
![]() ,
,
где ![]() ,
, ![]() – бикомплексные
функции, моногенные по бикомплексной функции
– бикомплексные
функции, моногенные по бикомплексной функции ![]() в области
в области ![]() .
.
Отметим,
что последняя формула является аналогом формулы Гурса для бигармонических
функций, которая выражает любую бигармоническую функцию через две аналитические
функции комплексной переменной ![]() [4].
[4].
Литература:
1.
Гусев В.А. Об одном обобщении ареолярных производных // Bul. stiint. al Instit. politehnic Timisoara, 1962.– Т. 7, f. 2.– P. 223-238.
2.
Федоров В.С. Основные
свойства обобщённых моногенных функций // Известия вузов. Математика, 1958. – №
6. – С. 257-265.
3.
Стельмашук Н.Т. О
некоторых линейных дифференциальных уравнениях в частных производных в дуальной
и бикомплексной алгебрах // Известия вузов. Математика, 1964.–№ 3.– С. 136-142.
4.
Смирнов В.И. Курс высшей математики.– М.:ГИТТЛ, 1953.– Т. 3.– Ч. 2.– С.
193-196.