Математика/5.Математическое моделирование
Н.С.Ибрагимов
Бакинский Государственный Университет
Необходимое условие в задаче идентификации
для нестационарного уравнения квазиоптики
Аннотация: В данной работе
изучается вопрос необходимого условия в
задаче идентификации об определении
комплекснозначного коэффициента
нестационарного уравнения квазиоптики.
При этом доказан принцип максимума Понтрягина и необходимое условие в виде вариационного неравенмтва.
Ключевые слова: Уравнения квазиоптики, задача
идентификации, принципа максимума
Понтрягина.
Введение
Задачи идентификации для нестационарного уравнения
квазиоптики часто возникают в нелинейной оптике при изучении процессов распространения
светового пучка в неоднородной среде, в которых неизвестными функциями обычно
являются показатели преломления и поглощения среды, а также начальная фаза
излученной волны [1]. Отметим, что ранее задачи идентификации об определении
фазы излученной волны для стационарного уравнения квазиоптики изучены, например,
в работах [1,2] и др, а задачи идентификации об определении вещественнозначного
коэффициента, то есть коэффициента преломления среды в стационарном уравнении
квазиоптики, другими словами, в нестационарном уравнении Шредингера ранее
исследованы, например, в работах [3-7] и др.
В данной работе изучается вопрос необходимых условий типа принципа
максимума Понтрягина и вариационного неравенства в задаче идентификации об определении комплекснозначного
коэффициента нестационарного уравнения квазиоптики. Следует отметить, что подобный
вопрос относительно задачи
идентификации для нестационарного уравнения квазиоптики впервые был изучен в
работе [8]. Однако настоящая задача по постановке и по классу решений
отличается от задачи из [8].
Постановка
задачи.
Пусть ![]() –ограниченная область
–ограниченная область ![]() - мерного евклидова
пространства
- мерного евклидова
пространства ![]() - граница области
- граница области ![]() , которая предполагается достаточно гладкой, например,
, которая предполагается достаточно гладкой, например, ![]() -заданные числа,
-заданные числа, ![]()
![]() -произвольная точка области
-произвольная точка области ![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,
, ![]() ,
, ![]() ;
;![]() -банахово пространство, состоящее из всех определенных и
-банахово пространство, состоящее из всех определенных и ![]() раз непрерывно
дифференцируемых функций на отрезке
раз непрерывно
дифференцируемых функций на отрезке ![]() со значениями в
банаховом пространстве
со значениями в
банаховом пространстве ![]() - лебегово пространство функций, суммируемых в области
- лебегово пространство функций, суммируемых в области ![]() со степенью
со степенью ![]() -соболевы пространства, которые
определены, например, в [9];
-соболевы пространства, которые
определены, например, в [9]; ![]() -гильбертово
пространство, состоящее из всех элементов
-гильбертово
пространство, состоящее из всех элементов ![]() из
из ![]() , имеющих
, имеющих ![]() из пространства
из пространства ![]() , скалярное произведение и
норма в нем определяются равенствами:
, скалярное произведение и
норма в нем определяются равенствами:
![]()
![]()
![]() -гильбертово пространство, состоящее из всех элементов
-гильбертово пространство, состоящее из всех элементов ![]() пространства
пространства ![]() имеющих обобщенные
производные
имеющих обобщенные
производные ![]() из пространства
из пространства ![]() . Скалярное произведение и норма в нем определяются
равенствами:
. Скалярное произведение и норма в нем определяются
равенствами:
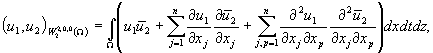
![]()
![]() ;
символ
;
символ ![]() означает «при почти
всех».
означает «при почти
всех».
Рассмотрим
задачу идентификации о минимизации функционала:
![]() (1)
(1)
на множестве ![]() при условиях
при условиях
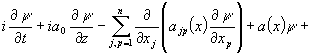
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() , (4)
, (4)
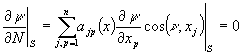 , (5)
, (5)
где ![]() -мнимая единица,
-мнимая единица, ![]() -внешняя нормаль границы
-внешняя нормаль границы![]() ,
, ![]() -волновая функция;
-волновая функция; ![]() заданные числа,
такие, что
заданные числа,
такие, что ![]() ,
, ![]() - заданные
функции, удовлетворяющие условиям:
- заданные
функции, удовлетворяющие условиям:
![]()
![]() С,
С, ![]() ;
(6)
;
(6)
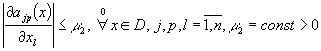 ;
(7)
;
(7)
![]() (8)
(8)
![]() ,
,![]() ,
,![]() -заданные комплекснозначные функции,
удовлетворяющие условиям:
-заданные комплекснозначные функции,
удовлетворяющие условиям:
![]()
![]() ,
, 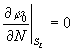 ,
, 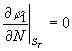 ,
,
![]() ,
, ![]()
![]() ; (9)
; (9)
![]() -заданный элемент,
-заданный элемент, ![]() .
.
При каждом ![]() задачу об определении
функции
задачу об определении
функции ![]() из условий (2)-(5) будем называть прямой задачей для
нестационарного уравнения квазиоптики (2). Под решением прямой задачи будем понимать функцию
из условий (2)-(5) будем называть прямой задачей для
нестационарного уравнения квазиоптики (2). Под решением прямой задачи будем понимать функцию ![]() из пространства
из пространства ![]() , удовлетворяющую условиям
(2)-(5) для почти всех
, удовлетворяющую условиям
(2)-(5) для почти всех ![]() . Прямая задача (2)-(5) ранее была изучена
в работе [10] и доказана:
. Прямая задача (2)-(5) ранее была изучена
в работе [10] и доказана:
Теорема 1. Пусть функции
![]()
![]()
![]()
![]() удовлетворяют условиям (6)-(9) соответственно. Тогда прямая
задача (2)-(5) при каждом
удовлетворяют условиям (6)-(9) соответственно. Тогда прямая
задача (2)-(5) при каждом ![]() имеет единственное
решение из пространства
имеет единственное
решение из пространства ![]() и для этого решения справедлива оценка:
и для этого решения справедлива оценка:
![]() . (10)
. (10)
Используя
эту теорему и методику работ [3-7] можно доказать и следующее утверждение:
Теорем
2. Пусть выполнены условия теоремы 1.
Пусть кроме того, функции ![]() ,
, ![]() удовлетворяют условиям (9), а
удовлетворяют условиям (9), а ![]() - заданный элемент. Тогда
задача идентификации (1)-(5) имеет хотя бы одно решение.
- заданный элемент. Тогда
задача идентификации (1)-(5) имеет хотя бы одно решение.
2. Необходимое условие типа принципа максимума
Понтрягина и вариационнго неравенства.
В
этом разделе будем изучить вопрос необходимого условия для решения задачи
идентификации (1)-(5). Пусть ![]() является решением
следующей сопряженной задачи:
является решением
следующей сопряженной задачи:
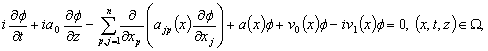 (11)
(11)
![]() , (12)
, (12)
![]() ,
(13)
,
(13)
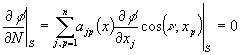 ,
(14)
,
(14)
где ![]() -
решение прямой задачи при
-
решение прямой задачи при ![]() .
.
Под решением сопряженной задачи будем понимать функцию ![]() из
из ![]() , удовлетворяющую
тождеству:
, удовлетворяющую
тождеству:
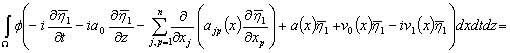
![]()
![]()
![]() (15)
(15)
для любой функции ![]()
![]() , удовлетворяющей условию
, удовлетворяющей условию ![]() .
.
С помощью замены ![]() сопряженную задачу (11)-(14) можно свести к
начально-краевой задаче, которая
является задачей типа комплексно сопряженной прямой задачи (2)-(5). Поэтому, используя методику сглаживания данных [9]
и теорему 1, можем установить справедливость утверждения о том, что сопряженная задача (11)-(14) имеет
единственное решение из пространства
сопряженную задачу (11)-(14) можно свести к
начально-краевой задаче, которая
является задачей типа комплексно сопряженной прямой задачи (2)-(5). Поэтому, используя методику сглаживания данных [9]
и теорему 1, можем установить справедливость утверждения о том, что сопряженная задача (11)-(14) имеет
единственное решение из пространства ![]() и справедлива оценка:
и справедлива оценка:
![]() (16)
(16)
для ![]() .
.
Введем функцию:
![]()
![]() , (17)
, (17)
которую будем называть
функцией Гамильтона-Понтрягина для задачи идентификации (1)-(5). Здесь ![]() .
.
Рассмотрим
приращение функционала (1) на любом элементе ![]() . Используя (1), приращение функционала можно представить в
виде:
. Используя (1), приращение функционала можно представить в
виде:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , (18)
, (18)
![]() , где
, где ![]() -приращение любого
элемента
-приращение любого
элемента ![]() такое,
такое, ![]() ,
, ![]() ;
; ![]() . Ясно, что функция
. Ясно, что функция ![]() является решением
следующей начально-краевой задачи:
является решением
следующей начально-краевой задачи:
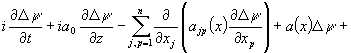
![]()
![]() , (19)
, (19)
![]()
![]() ,
, ![]() (20)
(20)
для
решения которой справедлива оценка:
![]() ,
,![]() . (21)
. (21)
Для преобразования
приращения функционала в дальнейшем нам понадобится следующее вспомогательное
утверждение:
Лемма 1. Справедливо соотношение:
![]()
![]()
![]()
![]()
![]()
![]() . (22)
. (22)
Доказательство этой леммы проводится с помощью сопряженной задачи (11)-(14) и начально-краевой задачи (19),(20) .
Используя аналог этой леммы, понятие квазисопряженной
системы и методику Плотникова В.И. [11], можем доказать необходимое условие в виде приципа
максимума Понтрягина Л.С. [12]:
Теорема 3. Пусть выполнены
условия теоремы 2. Для того, чтобы ![]() была решением задачи
(1)-(5) необходимо выполнение условия:
была решением задачи
(1)-(5) необходимо выполнение условия:
![]()
![]() (23)
(23)
для почти всех ![]() , где
, где ![]() ,
,![]() - соответственно решения прямой и сопряженной задач при
- соответственно решения прямой и сопряженной задач при ![]() .
.
Теперь укажем необходимое условие в виде вариационого
неравенства. С этой целью установим дифференцируемость функционала (1).
Используя формулу (18) для прирашения функционала и лемму 1, можем доказать следующее утверждение:
Теорема 4. Пусть
выполнены условия теоремы 2. Тогда функционал ![]() дифференцируем по
Фреше на множестве
дифференцируем по
Фреше на множестве ![]() и для его градиента
справедлива формула:
и для его градиента
справедлива формула:
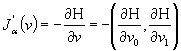 , (24)
, (24)
где ![]() - функция Гамильтона-Понтрягина.
- функция Гамильтона-Понтрягина.
С помощью этой теоремы
и известной теоремы из работы [13,
стр. 28] можем установить необходимое условие в виде вариационого неравенства:
Теорема 5. Пусть
выполнены условия теоремы 4. Пусть, кроме того, ![]() является любым
решением задачи идентификации (1)-(5). Тогда для любого
является любым
решением задачи идентификации (1)-(5). Тогда для любого ![]() справедливо
неравенство:
справедливо
неравенство:
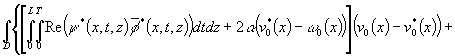
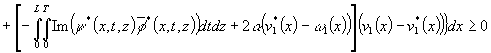 , (25)
, (25)
где ![]() ,
, ![]() - решения прямой и сопряженной задач при
- решения прямой и сопряженной задач при ![]() .
.
Литература
1. Воронцов
М.А., Шмальгаузен И.И. Принципы адаптивной оптики. М.: Наука, 1985. -335 с.
2. Шамеева
Т.Ю. Об оптимизации в задаче о распространении светового пучка в неоднородной
среде //Вести. Московск.ун-та. Сер.вычисл.матем.и киберн. -1985,№1.-с.12-19.
3. Искендеров
А.Д., Ягубов Г.Я. Вариационный метод решения обратной задачи об определении
квантовомеханического потенциала //ДАН СССР.-1988, т.303, №5. -с.1044-1048.
4. Искендеров
А.Д., Ягубов Г.Я. Оптимальное управление нелинейными кван-товомеханическими
системами //Автоматика и телемехан.-1989, №12. с.27-38.
5. Ягубов
Г.Я., Мусаева М.А. О вариационном методе решения методе решения многомерной
обратной задачи для нелинейного уравнения Шредингера //Изв.АН Азерб. Сер.физ-техн.и
матем.наук.-1994, т.XV, №5-6. -с.58-61.
6. Ягубов
Г.Я., Мусаева М.А. Об одной задаче идентификации для нелиней-ного уравнения
Шредингера//Дифференц. уравнения.-1997, т.33, №12. -с.1691-1698.
7. Искендеров
А.Д., Ягубов Г.Я. Оптимальное управление квантовомеха-ническим потенциалом
//Труды ИММ АНА. -1998, т.XVIII. -с.75-80.
8. Ягубов
Г.Я., Ибрагимов Н.С. Задача оптимального управления для нестационарного
уравнения квазиоптики //В сб.: «Проблемы матем.модел. и опт. управления». -Баку,
2001. -с.49-57.
9. Ладыженская
О.А. Краевые задачи математической физики. М.: Наука, 1973. -408 с.
10.
Искендеров А.Д., Ибрагимов Н.С. Разрешимость начально-краевых задач для
нестационарного уравнения квазиоптики // Вестник Ленкоранского гос. ун-та. Сер.
естественных наук, 2009, Ленкорань, с. 47-66.
11. Плотников В.И., Сикорская Е.Р.
Оптимизация управляемого обьекта, описываемого нелинейной системой
гиперболических уравнений // Изв. ВУЗов. Сер. Радиофизика.- 1972, т.15, №3.-
с.345-357.
12. Понтрягин
Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория
оптимальных процессов. М.: Наука, 1969. – 384 с.
13. Васильев
Ф.П. Методы решения экстремальных задач. М.:Наука, 1981.-400с
Ibrahimov N.S.
A necessary
condition in the problem of identification
for non stationary
equation of quasi optics.
Summary: In
this we study the question of necessary condition in the problem of
identification of the definition of complex- valued coefficient of non stationary equation quasi optics. This proved the maximum principle of Pontryagin and necessary condition in the
type variation inequality. Key words: Non stationary equation quasi optics, the identification
problem, the Pontryagin maximum principle.