Математика / Прикладная математика

А.К.Керимов, Р.И.Давудова, Г.С.Керимова

Азербайджанский Государственный Экономический Университет

Институту Кибернетики Национальной Академии Наук Азербайджана

Азербайджанская Государственная Нефтяная Академия

ОБ ОДНОМ ПОДХОДЕ РЕШЕНИЯ ЗАДАЧ

АВТОМАТИЧЕСКОЙ КЛАССИФИКАЦИИ

В работе рассматривается вопрос построения классификационного правила, являющееся оптимальным в том смысле, что его использование обеспечивает в среднем наименьшую вероятность совершения ошибки классификации при помощи статистического анализа.

1. Постановка задачи

Пусть имеется такая совокупность n объектов одной природы

, (1.1)

где каждый ее может быть описан n различными количественными признаками: где n-мерное Евклидово пространство. Далее, на основании теоретических соображений или предварительного анализа имеющихся данных предполагается, что исследуемая совокупность (1.1) не является однородной, ее элементы образуют отдельные сгустки, скопления –кластеры, классы. Тогда возникает задача о выделении этих классов – определении их числа, состава и некоторых характеристик.

2. Методы решения

Для решения поставленной задачи, данную совокупность (1.1) будем рассматривать как реализацию некоторой действительной n-мерной случайной величины с неизвестной плотностью вероятности f(X), которая представлена в виде конечной смеси к нормальных распределений с равными ковариационными матрицами S и различными векторами средних значений m_i , т.е.

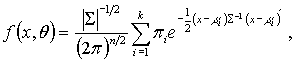(1.2)

где – вектор-строка, – вектор-столбец, S– действительная, симметричная, положительно определенная матрица, p_i – весовой коэффициент i-го распределения, удовлетворяющий условиям

.

Параметры смеси k и q считаем постоянными и неизвестными.

Множество допустимых значений r-мерного параметра смеси q обозначим через W :

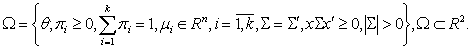
Эффективное использование конечных нормальных смесей в задачах классификации обусловлено, в первую очередь, таким их важным свойствам, как разделимость, или идентифицируемость. Под идентифицируемостью понимается возможности однозначного восстановления каждого из составляющих распределений

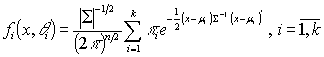(1.3)

по заданному распределению всей смеси (1.2). Свойство разделимости определяет принципиальную возможность решения задачи разделения наблюдений на классы. Кроме того, использование конечных смесей нормальных распределений в качестве функций, аппроксимирующих неизвестные плотности вероятностей, обусловливается как существованием в природе объектов с распределением (1.2) или близким к нему, так и полнотой системы Гауссовых функций вида в пространстве

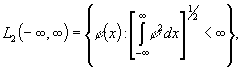
то есть возможностью их применения для представления достаточно широкого класса распределений.

Под классом, или образом мы будем понимать генеральную совокупность, описываемую функцией плотности вероятности (1.3). Тогда, чтобы выделить классы в данной совокупности (1.1) , необходимо в выражении (1.2) найти оптимальные оценки (наилучшие в некотором смысле) для неизвестных параметров k и q, а затем использовать их в статистических решающих правилах для разнесения наблюдений по классам. Каждый класс обозначим через

При известном значении k, 1<k<n оптимальную оценку для можно найти как решение системы уравнений правдоподобия, используя алгоритм D_ЭЯ (Шлезингера) при k>2. Доказано, что если функция правдоподобия

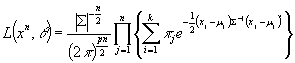(1.4)

ограничена, то алгоритм D_ЭЯ сходится к таким оценкам максимального правдоподобия которые являются точками локальных максимумов или седловыми точками поверхности (1.4). известно также , что при довольно слабых условиях регулярности функции плотности f(x,θ) среди множества решений системы уравнений правдоподобия существует одно оптимальное решение, и что в нем матрица отрицательно определена по вероятности, т.е. функция правдоподобия при имеет локальный максимум. Условия регулярности следующие: а) существуют непрерывные частные производные почти для всех и для всех некоторая окрестность точки истинного значения параметра б) регулярна в смысле ее первых и вторых частных производных по компонентам параметра , т.е.

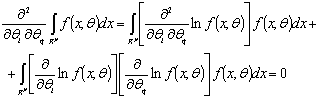
Легко проверить, что приведенные условия регулярности выполняются для функции (1.2). В том случае, когда система уравнений правдоподобия имеет несколько решений , единственным опознавательным признаком оптимального решения является наличие локального максимума у логарифмической функции правдоподобия при .

Далее, при использовании алгоритма D_ЭЯ в задачах классификации наблюдений необходимо установить насколько сильно зависит вероятность получения оптимального решения от таких факторов, как размерность выборочного пространства, объем выборок, расстояния между классами и др. Задача классификации наблюдений из смеси к нормальных распределений (1.2) не вызывает принципиальных затруднений при известном значении k. Если же число k неизвестно, то это задача становится одной из наиболее сложных задач классификации. Определение наиболее вероятного значения k по данным наблюдениям мы свели к последовательной проверке двух сложных гипотез H_k и H_k+1, l<<n, где H_k исследуемая совокупность (1.1) есть смесь к нормальных классам. В ходе последовательной проверки этих гипотез принимается та гипотеза H_k, которая первой согласуется данными наблюдениями.

Литература

1. Дж.Ту, Р.Гонсалес. Принципы распознавания образов. М., ‘‘Мир’’, 1978.

2. Р.Дуда, Р.Харт. Распознавания образов и анализ сцен. М., ‘‘Мир’’, 1976.