Reduction of thermal
noise in system of magnetic nanoparticles
under asymmetric stochastic resonance conditions
A.G. Isavnin, I.I.Mirgazov
Kazan (Volga region) Federal University, Russia
Stochastic resonance effect is previous quite sharp increase and subsequent
gradual decay of response of a multistable system to a weak periodic modulation
as internal noise of the system goes up [1]. Such a phenomenon is well explored
both theoretically and experimentally within wide range of applications, from
global climatic changes to nervous processes in live organisms [2]. Generally
external periodic signal is assumed to be weak, so without noise any
transitions between stable states of the system are impossible. At a certain
noise intensity regular part of dynamics of the system increases, that is the
transformation of stochastic energy into coherent one occurs. The two-state
theory says that for a bistable system the response reaches its maximum when
mean time of transitions between stable states becomes comparable to a half of
period of modulation. At greater noise intensities the coherency of signal and
noise fails and the response goes down.
Monodomain magnetic particles with «easy axis» anisotropy are bistable
elements with steady states associated with two opposite directions of easy
axis. Such nanoparticles are technologically important materials and their
unique properties continuously attract attention of scientists. In previous
papers stochastic resonance was considered in fine magnetic particles for thermal
[3,4] and tunneling [5,6] modes of magnetization reversal. Obtained results
displayed specific non-monotonous dependence of the response to radiofrequency
signal on the noise level. Values of signal-to-noise ratio and components of
dynamic magnetic susceptibility derived within the two-state approximation were
verified by means of numerical calculations [7,8], based on a Fokker-Planck
equation with periodic drift term.
Present paper considers the influence of additional external magnetic
field applied at arbitrary angle ![]() to the easy
axis on output noise power as stochastic resonance rises.
to the easy
axis on output noise power as stochastic resonance rises.
Energy of the uniaxial monodomain particle under such circumstances is ![]() . (1)
. (1)
The first here term describes interaction of the magnetic moment of
superparamagnetic particle with anisotropy field (K is anisotropy constant, v
is the particle’s volume, q is the angle between
magnetization vector and easy axis), the second term is associated with
permanent magnetic field Í that distorts
symmetry of the double-well potential.
We, like in [4], associate input signal with external radiofrequency
field and input noise with temperature T of the sample. Then output of the
system is change of the magnetic moment.
The external periodic signal is assumed to be weak enough, so it alone
cannot lead to changes of direction of the particle’s magnetic moment. This implies
the condition m0MH1v < DU holds. Thermal
activation of the system increases rate of switches of the particle’s magnetic
moment and that leads to possibility to surmount the potential barrier.
Further the discrete-orientations approximation is used in the
calculations. Therefore the magnetic moment of the particle is allowed to be in
just two states corresponding two minima of the double well. So the stable
states are for x=Mcosq at q1
, q2 . The two-state theory used trough this paper implies that instead of
continuous diffusion of the particle’s magnetic moment over a sphere we
consider its stochastic switches between two directions. Advantage of such
approximation is possibility of using the master equation for transition rates
that yields analytical solution. The master equation is [1,4]:
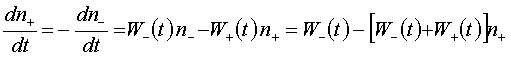 . (2)
. (2)
Here n± is the probability of
discrete variable x=Ìcosq to take value x± = Ì1,2. W±(t) are escape rates
from the states corresponding to stable directions of the magnetic moment at
angles q1, q2 to the easy axis.
Such rates are described with Kramers-type formula [9, 4]:
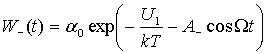 ,
, 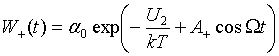 . (3)
. (3)
Here ![]() ,
, ![]() are heights of the potential
barriers. As it was shown in [3],
are heights of the potential
barriers. As it was shown in [3], ![]() , provided
, provided ![]() , so for
simplification of our calculations let us assume
, so for
simplification of our calculations let us assume ![]() . Here
. Here ![]() is dimensionless amplitude
of external modulation on the easy axis. Let us also denote
is dimensionless amplitude
of external modulation on the easy axis. Let us also denote ![]() .
. 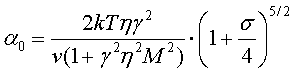 , (4)
, (4)
is the attempt frequency, and ![]() [10],
[10], ![]() is the gyromagnetic ratio,
is the gyromagnetic ratio, ![]() is a damping constant from the Hilbert equation [9].
is a damping constant from the Hilbert equation [9].
Power spectrum of
the system as Fourier transform of the autocorrelation function displays Lorentzian background associated with
stochastic dynamics and d - spike describing regular
motion of the vector M at the frequency W of external signal: 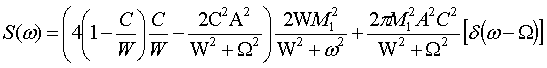 . (5)
. (5)
Here 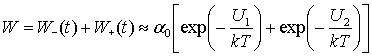 ,
, 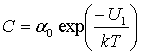 is Kramers rate of escape from the lower minimum of
the asymmetric nonmodulated potential.
is Kramers rate of escape from the lower minimum of
the asymmetric nonmodulated potential. ![]() is phase shift between
response of the system and external periodic signal.
is phase shift between
response of the system and external periodic signal.
Output power of the system can be obtained by means of integrating (9)
over w from 0 to ¥ [11]:
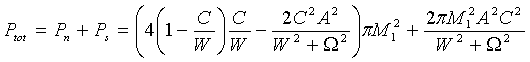 . (6)
. (6)
Here the first term describes
output noise power, and the second one is associated with output signal of the
system. It is obvious that the noise power diminishes to the same value as the
signal power increases. So there is transformation of chaotic motion energy
into coherent one.
The following reduced result
(ratio of output noise power of the modulated system to output noise power of
the non-modulated system)
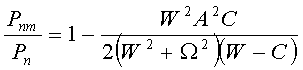 , (7)
, (7)
reveals non-monotonous dependence on temperature with a distinct minimum,
see Figure 1.
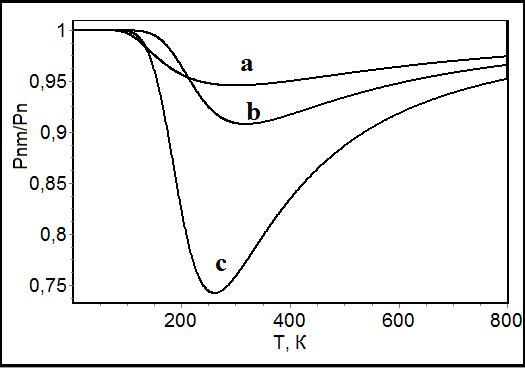
Figure 1. Pnm/Pn vs temperature. Parameters of the system: Ω=1E5 ñ-1, v=5.5E-25 ì3, M=1.72E6 A/ì, Í1=3000 À/ì, H=10000 À/ì, a) α=900,
b) α=800, c) α=700
REFERENCES
1. McNamara B., Wiesenfeld K. // Phys.Rev.A (1989), V.39, N
9, P.4854-4869.
2. Wiesenfeld K.,
Pierson D., Pantazelou E., Dames C.,
Moss F. // Phys.Rev.Lett. (1994), V.72, P.2125-2129.
3. Sadykov E.K. //
J.Physics: Conden. Matt. (1992), V.4, P.3295-3298.
4. Sadykov E.K.,
Isavnin A.G. // Physics of the Solid State
(1994), V.36, N 11, P.1843-1844.
5. Sadykov E.K.,
Isavnin A.G., Boldenkov A.B. // Physics of the Solid State (1998), V.40, N 3,
P.474-476.
6. Isavnin A.G. //
Physics of the Solid State (2001), V.43, N 7, P.1263-1266.
7. Sadykov E.K.,
Isavnin A.G. // Hyperfine Interactions (1996), V.99, P.415-419.
8. Isavnin A.G. //
Russian Physics Journal (2002), V.45, N 11, P.1110-1114.
9. Brown W.F.(jr.) //
Phys.Rev. (1963), V.130, N 5, P.1677-1686.
10. Isavnin A.G. // Russian Physics Journal (2007), V.50,
N 5, P.471-476.
11. Isavnin A.G. // Physics
of the Solid State (2002), V. 44, N 7, P.1336-1338.