ТЕХНИЧЕСКИЕ НАУКИ/12. Автоматизированные

системы управления на производстве

Д.т.н. Бондаревский А.С.

ОАО «Ангстрем-М», г. Москва, Зеленоград, Россия

Многомерные метрологические шкалы и операции

измерений, контроля, испытаний, идентификации

В известной гносеологической триаде В.И. Ленина, - «от живого созерцания к абстрактному мышлению и от него к практике», первая треть выражает начало познания, - восприятие самости-качества того или иного объекта познания. Здесь, восприятие, - как построение информационной, ниже, - математической, модели познаваемого качества. Последовательно проходимыми реперами такого восприятия являются: самость-качество - его физическая модель-свойство [1] (локальная, - в познаваемом отношении, «грань»-признак качества, здесь, - физическая модель качества) - математическая модель свойства (она же, таким образом, опосредованно, - математическая модель качества).

Интерпретируем выделенную последовательность реперов «качество-свойство-математическая модель качества», как совокупность их структур и (&) их определённостей-значений, Тогда имеющее место множество значений структуры свойства есть то, что в [2] и других, более поздних, источниках именуется, как «эмпирическая система». Здесь, - эмпирическая система свойства. Сюда же, как оказывается, следует присовокупить ещё и, будем говорить, «эмпирическую систему качества», - множество отвечающих эмпирической системе свойства прообразов, - значений структуры качества. В свою очередь, множество значений структуры математической модели качества есть то, что в [2 ] и др. 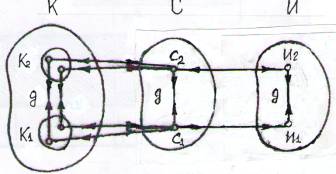именуется, как «математическая», или «знаковая система». При этом если между множеством значений структуры качества (множеством «значений К качества», - эмпирической системой качества) и множеством значений структуры свойства (множеством «значений С свойства», - эмпирической системой свойства) имеет место гомоморфное отображение [3], - рис.1, то между множеством значений С свойства (эмпирической системой свойства) и множеством значений структуры математической модели качества (множеством «значений И математической модели качества, - «знаковой системой») имеет место, на этот раз, уже изоморфное отображение [3], - рис.1., где, как g, обозначены сохраняемые при переходе от множеств К к С, и от С к И бинарные отношения [3] элементов этих множеств, - значений реперов триады «качество-свойство-математическая модель качества».

Далее отметим [1,4], что свойства бывают простые-одномерные-«нераспа

дающиеся» (ниже, - «свойства»), здесь, - одномерные интенсивности- физичес-

кие величины, и сложные-многомерн-

ые, - векторы простых.

Рис. 1 При этом структуры отмеченных прос-

тых и сложных свойств описываются тетрадой так называемых функторов [5], именуемых: в случае простого свойства, - «свойством» (тождественным функтором), в случае сложных свойств: двумерного, - парой: «свойство» - «свойство» («функтором»); трёхмерного, - парой: «cвойство» - «функтор»; четырёхмерного, - парой: «функтор» -«функтор» и т.д. (здесь «и т.д.» - свойства более, чем четырёхмерные, на практике не рассматриваются).

Поименуем информационные образы функторов свойства выделенной тетрады [здесь, как получается, - их (функторов свойства) математические модели и, таким образом, - «математические модели качества»] «информационными характеристиками». Тогда, очевидно, что эти характеристики находятся во взаимно однозначном (биективном [3]) отношении с поименованными выше структурами свойств, - функторами свойств приведенной выше, таким образом, физической тетрады и представляют собой, на этот раз, уже некую информационную тетраду. В данном случае такую тетраду, как [4]: «размер» - пара «размер»-«размер» («функция») - пара «размер»-«функция» («функционал») - пара «функция»-«функция» («оператор»). Понятие этой тетрады, - поименуем её, как таковую Темникова-Розенберга [4], навеяно идеями этих учёных. (Ф.Я. Темников, профессор МЭИ, - один из основоположников информатики, специалист в области автоматики, телемеханики и теории информации. В.Я. Розенберг, - профессор МФТИ, - специалист в области радиотехники, метрологии и теории массового обслуживания).

А теперь проиллюстрируем в табл. 1 соответствие приведенных выше понятий свойств, структур свойств и значений структур свойств (физических реалий), с одной стороны, и отвечающих им информационных характеристик и их (информационных характеристик) значений, с другой.

Таблица 1.

Свойства- физические модели качества (структуры & значения К)	Структуры (функторы) свойств - физическая тетрада с значениями С - «эмпирической системой»	Информационные характеристики структур-функторов свойств (информационная тетрада Темникова-Розенберга)]	Значения И информационных характеристик («знаковая система»)
Простые (одномерные)	«Свойство»	«Размер»	Состоят в отношениях, выражаемых одномерными метрологическими шкалами С. Стивенса, П. Суппеса, Дж. Зинеса [2,6]
Сложные (много: дву, трёх- и четырёхмерные)	Пара: «свойство» - «свойство» («функтор»)	Пара: «размер» - «размер» («функция»)	Состоят в отношениях, выражаемых многомерными метрологическими шкалами
	Пара: «cвойство»- «функтор»	Пара: «размер» - «функция» («функционал»)
	Пара: «функтор» - «функтор»	Пара: «функция» - «функция» («оператор»)

Как следует из рис. 1, значения качества К и свойства С являются гомоморфными. А далее, - табл. 1, значения С и И колонок 2 и 4 являются изоморфными. А это значит, что бинарные отношения между значениями И той или иной из математических моделей, - отношения в «знаковой системе», полностью передают отношения значений С (значений «эмпирической системы) порождающих эти модели свойств, а через них, - передают отношения значений К познаваемых качеств (обоснование проявляемости познаваемых качеств в получающихся математических моделях свойств и, таким образом, - возможности именования их математическими моделями качеств). В табл. 1 показано, что отношения всех рассмотренных значений (таковых качества, свойства и их математических моделей) выражаются так называемыми метрологическими шкалами (ниже, - «шкалами»), - разновидностями этих отношений.

А теперь обратим внимание на то, что известная в настоящее время теория шкал {в данном случае, - таковых неметрических (наименований, порядка) и метрических (разностей, отношений, абсолютных)] [7]}, основанная в 1946 - 1967 гг. американскими психологами С. Стивенсом, П. Суппесом, Дж. Зинесом, распространяется только на верхнюю строку в табл. 1, - т.е. современная теория шкал распространяется только на простые свойства-физические величины. А это значит, что современная теория шкал не распространяется на три нижних строчки табл.1, т.е. она, таким образом, не распространяется на сложные, - многомерные, свойства. А это значит, что, если современная теория шкал охватывает, таким образом, информационные операции [4] измерений (метрические шкалы [7]) и контроля (неметрические шкалы [7]), то она совершенно не охватывает такие незаменимые при познании сложных (здесь, дву-, трёх- и четырёхмерных - табл. 1) свойств информационных операций, как измерительные (определительные), контрольные испытания [познание дву- (ГОСТ 16504-81) и трёхмерных свойств] и идентификация {познание четырёхмерных свойств, - например, восприятие функциональных операторов в метрическом пространстве [8], здесь, - количественная (статических [9], динамических [10] характеристик объектов) и качественная идентификация}.

И, наконец, обратим внимание на то, что если в случае простых (одномерных) свойств-физических величин шкалы (таким образом, - одномерные) представляют собой отношения значений (чисел, событий) такой информационной характеристики структуры простого свойства, как размер, то в случае сложных (многомерных) свойств-векторов шкалы (таким образом, - многомерные) должны, соответственно, представлять собой отношения значений таких информационных характеристик структуры сложных свойств, как функция, функционал и оператор. Но это возможно сделать только в том случае, если названное понятие «отношения» применить не непосредственно к этим значениям, а к значениям норм названных функции, функционала, оператора в соответствующих функциональных пространствах [8].

Заключение.

Современная теория шкал распространяется на простые (одномерные) свойства-физические величины и не распространяется на сложные (многомерные, - вектора простых) свойства. А это значит, что современная теория шкал охватывает только информационные операции измерений (метрические шкалы) и контроля (неметрические шкалы). Но она не охватывает такие воспринимающие сложные свойства информационные операции, как измерительные (определительные), контрольные испытания и идентификация. Как оказывается, в случае сложных свойств соответствующие многомерные шкалы должны представлять собой не, как в случае простых свойств-физических величин, отношения определённостей-значений (чисел, событий) такой информационной характеристики, как размер, и не отношения определённостей-значений таких информационных характеристик структуры сложных свойств, как функция, функционал, оператор. В случае сложных свойств соответствующие многомерные шкалы должны представлять собой отношения значений норм этих характеристик в соответствующих функциональных пространствах.

Литература.

1. Бондаревский А.С. Информационная экспликация категорий качества и свойства // Современные наукоёмкие технологии, - N 6, 2008

2. Стивенс С.С. Математика, измерение и психофизика // Экспериментальная психология. - М.: ИИЛ, 1960

3. Шрейдер Ю.А. Равенство, сходство, порядок. - М.: Наука, 1971

4. Бондаревский А.С. Информационные операции: понятие, канонические классы и виды // Международный журнал прикладных и фундаментальных исследований. - N 8, 2011

5. Букур И., Деляну А. Введение в теорию категорий и функторов, - М.: Электронная библитека механико-математического факультета МГУ, 1972

6. Суппес П., Зинес Дж. Основы теории измерений // Сб. Психологические измерения. - М.: Мир, 1967.

7. Кузнецов В.А., Ялунина Г.В. Основы метрологии, - М.: Изд-во стандартов, 1995.

8. Вулих Б.З. Введение в функциональный анализ. - М.: Наука, 1967

9. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Множественная регрессия. - М.: «Диалектика», 2007

10. Льюнг Л. Идентификация систем. Теория для пользователя. - М.: Наука, 1991