С. А. Оганисян
Государственный
инженерный университет Армении
Применение теории качественной
обратной связи в многомерных системах управления
В теории автоматического управления существуют
методы, которые позволяют учитывать параметрические неопределенности в системах
с обратной связью. Одним из таких методов является теория качественной обратной
связи (КОС), предложенная И. Горовицем [1,2,3]. Теория КОС широко применяется в одномерных системах регулирования,
но в многомерных системах автоматического регулирования (МСАР) использование
этой теории к настоящему времени носит ограниченный характер. Для применения
теории КОС к многомерным системам в работе предлагается воспользоваться методом
характеристических передаточных функций (ХПФ) [4] .
Рассмотрим
однотипную МСАР, матричная структурная схема которой представлена на
рис. 1. В таких МСАР сепаратные каналы имеют одинаковые передаточные функции, а
взаимные связи между каналами являются жесткими и характеризуются вещественной
числовой матрицей. Однотипные МСАР широко распространены в различных
технических приложениях, например, в аэрокосмической технике, химической
промышленности и других.
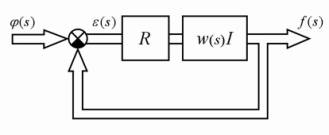
Рис. 1 Обшая структурная схема однотипной МСАР
На рис. 1: ![]() ,
, ![]() и
и ![]() -
- ![]() -мерные векторы входа, ошибки и выхода,
-мерные векторы входа, ошибки и выхода, ![]() -
- ![]() матрица жестких
взаимных связей,
матрица жестких
взаимных связей, ![]() - передаточная
функция отдельных каналов.
- передаточная
функция отдельных каналов.
Будем считать, что матрица ![]() неопределена, то есть
неопределена, то есть
![]() , (1)
, (1)
где
![]() элементы матрицы
элементы матрицы ![]() .
.
Для применения класической теории КОС к МСАР воспользуемся
методом ХПФ. Согласно этому методу,
передаточную матрицу разомкнутой системы ![]() можно представить в
виде
можно представить в
виде
![]() , (2)
, (2)
где
![]() - собственные
значения матрицы
- собственные
значения матрицы ![]() ;
; ![]() - соответствующие
собственные векторы;
- соответствующие
собственные векторы; ![]() - модальная матрица,
составленная из векторов
- модальная матрица,
составленная из векторов ![]() ;
; ![]() называются
характеристическими передаточными функциями. С помощью ХПФ
называются
характеристическими передаточными функциями. С помощью ХПФ ![]()
![]() -мерная МСАР может быть представлена как совокупность
-мерная МСАР может быть представлена как совокупность ![]() независимых одномерных
систем, к которым можно применить теорию КОС с использованием диаграмм Никольса.
независимых одномерных
систем, к которым можно применить теорию КОС с использованием диаграмм Никольса.
Поясним применение теории на конкретном примере.
Пример.
Рассмотрим двумерную однотипную МСАР, которая представлена на рис 2, где ![]() статический
регулятор, передаточная функция
статический
регулятор, передаточная функция ![]() имеет вид
имеет вид
![]() ,
(3)
,
(3)
а матрица ![]() равна
равна
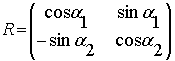 . (4)
. (4)
Углы ![]() и
и ![]() в матрице
в матрице ![]() могут принимать
значения в некоторых областях
могут принимать
значения в некоторых областях ![]() ,
, ![]() : Зона неопределенности показана на рис. 3.
: Зона неопределенности показана на рис. 3.
Ставится следующая задача: выбрать коэффициент
регулятора ![]() так, чтобы система
была устойчивой, а её показатель колебательности по отношению к вектору ошибки
не превышал значение
так, чтобы система
была устойчивой, а её показатель колебательности по отношению к вектору ошибки
не превышал значение ![]() . Для решения задачи следует на диаграмме Никольса построить характеристический
годограф разомкнутой системы, и
запретные окружности для заданнного значения
. Для решения задачи следует на диаграмме Никольса построить характеристический
годограф разомкнутой системы, и
запретные окружности для заданнного значения ![]() и граничных значений неопределенных параметров.
и граничных значений неопределенных параметров.
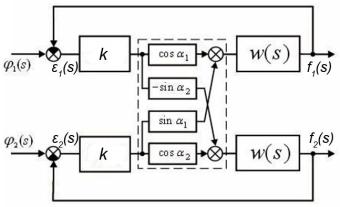
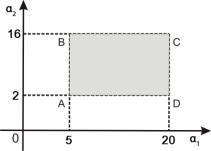
Рис. 2 Структурная схема двухмерной Рис.3 Зона неопределенности
однотипной МСАР
На рис. 4 на диаграмме Никольса построены
годограф ![]() для
для ![]() (линия 1) и
(линия 1) и ![]() (линия 2), точки
(линия 2), точки ![]() для углов
для углов ![]() и
и ![]() , соответствующих конечным точкам зоны неопределенности, и запретные
зоны для
, соответствующих конечным точкам зоны неопределенности, и запретные
зоны для ![]() (отбражения окружностей
на плоскость диаграмм Никольса).
(отбражения окружностей
на плоскость диаграмм Никольса).
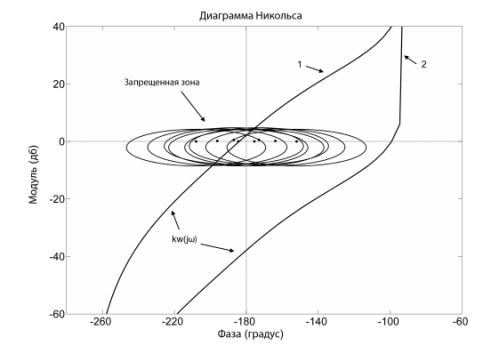
Рис. 4 Диаграмма Никольса
Для устойчивости системы необходимо, чтобы
годограф ![]() не охватывал точки
не охватывал точки ![]() и находился вне зоны
запретных окружностей.
и находился вне зоны
запретных окружностей.
Из рис. 4 видно, что система при ![]() неустойчива, а при
неустойчива, а при ![]() - устойчива. Следовательно,
при
- устойчива. Следовательно,
при ![]() и заданной непределенности
матрицы взаимных связей задача решена и система является устойчивой.
и заданной непределенности
матрицы взаимных связей задача решена и система является устойчивой.
Рассмотренный подход применим к однотипным МСАР
любой размерности.
Литература
1. Isaac Horowitz, Invited paper Survey of quantitative feedback theory
(QFT), INT.J, CONTROL, 1991, vol. 53, No. 2, 255-291
2. Isaac M. Horowitz, Marcel Sidi, Synthesis of feedback systems with large
plant ignorance for prescribed time-domain tolerances, INT. J. CONTROL, 1972,
vol. 16, No.2,287-300
3. Constantine H. Houpis, Steven J. Rasmussen, Quantitative feedback
theory: fundamentals and applications, 1999 by Marcel Dekker, Inc.
4. Гаспарян О. Н., Теория
многосвязных систем автоматического регулирования, ГИУА, Изд.-во “Асогик”,
Ереван, 2010.