ФУНКЦИОНАЛЬНЫЕ МЕТОДЫ ЛОГИЧЕСКОГО ВЫВОДА

к. ф.-м. н., доц. Евсеев В.И.

Казанский (приволжский) федеральный университет,

кафедра прикладной информатики

vladislaw.evseev@yandex.ru

 

1.Функциональное обоснование правил вывода

1. Общая схема правила вывода может быть формализована в следующем виде:

.

(1)

 Формула (1) имеет смысл выводимости из посылок Q1(А,В,С,...),... Qп(А,В,С, ...) при условии их одновременной истинности, логического след­ствия S(А, В, С, ...).

Таким образом, мы приходим к методу проверки правила вывода: полагая, что

=1, ..., =1.

одновременно нужно доказать выполнение =1 при любых допустимых значениях А, В, С, ... .

Схемы натурального вывода в зависимости от числа входящих в посылки операций, подразделяются на бинарный, тернарный, дважды бинарный (и т.д.) уровни.

Рассмотрим некоторые примеры проверки формул натурального вывода предложенным методом.

2. Рассмотрим классические модусы в системе вывода:

а) modus ponens (утверждающий тип)

,

 

 б) modus tollens (отрицающий тип)

.                                                 

 

                                   a)

б) .

 

 

Проведём анализ первого выражения . Для его анализа получаем из условий посылок

 (А ® С) = 1 –  (А) +  (А)· (С);

полагая  (А ® С) = 1, находим

  (А) =  (А) ·(С).

Аналогично

 (В® С)=1 –  (В) + (В)·   (С);

 

Учитывая, что (В ® С) = 1, имеем

/

Выводя следствие, получаем

 (А  В) = (А) + (В) –  (А)· (В),

((А В) ® С) = 1 – (А  В) () =1 –  (А В) +  (А  В)  (С)            = 1 – (А) – (В) +   (А)·  (В) + (А)·  (С) + (В)· (С) –

 (А)· (В)· (С) = 1– [ (А) – (А)· (С)]– [(В) – (В)·  (С)]+    (А)[ ( В) – (В)· (С)] = 1

 

Выделенные выражения в скобках равны нулю в силу условий посылок, поэтому формула доказана.

2. Функциональные методы анализа умозаключений

1. Разделительные умозаключения подразделяются на категорические и условные.

Рассмотрим сначала два основных вида категорических  разделительных умозаключения.

а) Отрицающе-утверждающий тип (modus toliendo ponens):

1 форма

((А  В) & ) ® В;

(3)

 2 форма

((А  В) & ) ® А.

(4)

 б) Строго разделительный тип (modus pomendo toliens):

1 форма

((AB) & А) ® ;

(5)

 2 форма

((АВ) & ) ® В.

(6)

2. Проведем проверку формулы (3).

Введем стандартные обозначения:

Q = А В;    S = Q & ;    Т = S ® В.

Для значений функций истинности получаем

q = а + b – аb;     s = b – аb;

отсюда следует

t = 1 – s + sb = 1 – b + аb + b – аb = 1.

Значит, Т – тавтология.

Отметим, что этот модус (как и все остальные) можно записать в форме правила вывода

МТР (1 форма):                           .

 Проверку остальных случаев рекомендуем провести читателям самостоятельно.

3. Условно-разделительные умозаключения называются дилеммами.

Рассмотрим два основных случая дилемм:

а) простая конструктивная дилемма

(((А ® В) & (С ® В)) & (А  С)) ® В;

(7)

б) простая деструктивная дилемма

(((А ® В) & (А ® С)) & ()) ® .

(8)

Проведем анализ простой конструктивной дилеммы (3.5.5). Обозначая:

Q = А ® В,    S = С ® В,     М = А С,   N = Q & S & М,   Т= N® В, –

получаем для функций истинности

q =1 – а*аb,    s = 1 – с + bс,    m =а+с – ас,    n= qsm,    t = 1 – t + nb.

Вычисления приводят к результату:

n = bс – ас + аbс,                                                                                               t = 1 – ас(1 – b).

Следовательно, данная формула имеет «дефектный блок» (А &  & С), значит тавтологией не является. Поэтому запишем простую конструктивную дилемму в форме правила вывода, определяя формулой:

ПКД:                    .

(8)

В этой форме ПКД является выводимой. Действительно, так как

I(А ® В) = 1, то а = аb;                                                                               I(С ® В) = 1, то с = bс;                                                                               I(А  С) = 1, то а + с – ас = 1.

При этом

t = 1 – ас(1 – b) = 1 – ас + аbс,

но с = bс,  то есть

t  = 1 – аbс + аbс = 1.

Значит, ПКД является законом логики только в форме (3.5.7).

Аналогично можно показать, что простая деструктивная дилемма не является тавтологией, но становится выводимой в форме

ПДД:                       .

(9)

3. Функциональные методы в анализе полисиллогизмов

1. Логически обусловленные или взаимосвязанные последовательности (цепочки) силлогизмов образуют полисиллогизмы.

Рассмотрим их основные виды:

а) эпихейрема (в форме правила вывода)

ЭП:                       ;

(10)

 б) прогрессивный сорит

ПС:                       ;

(11)

 в) регрессивный сорит

РС:                       ;

(12)

г) прогрессивный полисиллогизм

ППС:                       ;

(13)

д) регрессивный полисиллогизм

РПС:                       .

(14)

Их проверка проводится по методике правил вывода .

2. Рассмотрим  методику проверки эпихейремы.

По условиям правила вывода:

  (В ® С) = 1, значит, b = bс;

[напомним, что (B ® С) = 1 – b + bс],

(А ® В) = 1, значит, а = аb;                                                                       ((Q ® А) = 1, значит, q = аq;                          (15)                                                                 (D ® Q) = 1, значит, d = dq.

Это – условия посылок. Из них нужно вывести следствие. Для следствия получаем

( D ® С) = 1 – d + dс.

Теперь «поднимаемся» по системе указанных равенств, конструируя значение функции d = (D):

                   d = dq = dаq = dаbq = dаbсq.

Подставляем найденное значение в формулу следствия:

(D ® С) = 1 – dаbсq + dаbсq · с = 1,

так как подчеркнутые слагаемые взаимно уничтожаются.

3. Аналогично проводится проверка прогрессивного сорита

Составляем условия посылок:

(А ® В) = 1, значит, а = аb;                                                                        (С ® А) = 1, значит, с = ас;               (16)                                                           (D ® С) = 1, значит, d = dс;

(Q ® D) = 1, значит, q = dq.

Функция истинности следствия имеет вид:

(Q ® В) = 1 – q + qb.

Теперь конструируем усложненное значение «q», перемещаясь по системе построенных равенств:

q = dq = dсq = dасq = dаbсq.

Это значение q подставляем в функцию  (Q ® В):

(Q ® В) = 1 – dаbсq + dаbсq · b = 1.

 4. Регрессивный сорит может быть записан и доказан в форме тавтологии:

(((А ® В) & В ® С)) & (С ® D)) ® (А ® D).

(17)

Введем обозначения:

Р = А ® В;   Q = В ® С;   S = С ® D;   N = Р & Q;                                    М = N & S;   R = А ® D;   Т = М ® R.

Для соответствующих функций истинности получаем:

р  = 1 – а + аb;   q = 1 – b + bс;   n = рq;                                                       s = 1 – с + сd;   r = 1 – а + аd;   m = ns;   t = 1 – m + mr.

Отсюда следует:

n = 1 – а – b + bс + аb;                                                                                 m = 1 – а – b – с + bс + аb + ас + сd – аbс – асd + аbсd.

Теперь для значения функции истинности следствия получаем

t = 1 – m + mr = 1 – m + m +                                                                           + (-а + аd)(1 – а – b – с + bс+ аb + ас + аd – аbс  – асd + аbсd).

Раскрывая скобки и приводя подобные члены, окончательно получаем t = 1. Таким образом, (Т) = 1,  то есть, Т – тавтология (закон логики).

Заметим, что эпихейрема также может быть доказана как тавтология (закон логики). В то же время прогрессивный и регрессивный полисиллогизмы тавтологиями не являются, но представляют собой выводимые формулы.

Проверка методом тавтологии для логических функций многих переменных представляет чисто технические трудности, и сам результат оказывается непрогнозируемым.

 

                            Литература:

 

1.    Евсеев В.И. Матричные методы  в логике. Учебно-методическое пособие. Казань. 2014 г.

2.    ЕвсеевВ.И. Логика. Монография. Изд.ТАРИ. Казань. 2001 г.
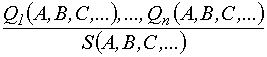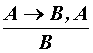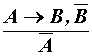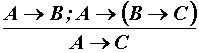
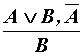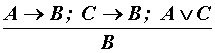
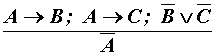
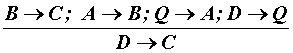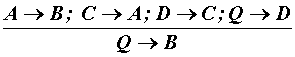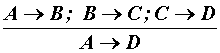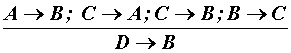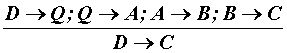