С.К. Лисин к.т.н., А. И. Федотов д.т.н.

СПб национальный минерально-сырьевой университет «Горный», СПб государственный политехнический университет, Россия

ИССЛЕДОВАНИЕ АНАЛОГОВЫХ МОДЕЛЕЙ ВОСПРОИЗВЕДЕНИЯ

ПАРАМЕТРОВ ПРЕЦИЗИОННЫХ ИЗМЕРЕНИЙ

Необходимость повышения точности, надежности, эффективности использования, создаваемых средств контактного контроля, связана с проведением анализа и синтеза элементной структуры измерительных механизмов. В процессе измерения преобразователи контактного типа (кодовые, индуктивные, цифровые …) получают непрерывную информацию при непосредственной связи измерительного наконечника с поверхностью объекта измерения. Поэтому достоверность воспроизведения входной измеряемой величины оценивается в процессе анализа точности измерительных механизмов.

Широко распространенными измерительными механизмами, используемыми в средствах управляющего и универсального контактного контроля, являются рычажные или рычажно-зубчатые механизмы. Конструкция рычажно-зубчатого измерительного прибора содержит измерительный стержень, измерительный механизм и шкальное или цифровое отсчетные устройства. Определение параметров измерительных механизмов аналоговых средств измерений, свидетельствует о целесообразности рассмотрения их моделей [1-4]. Подобные измерительные механизмы, содержащие синусно-кулисные передачи, преобразуют вращательное движение синусной передачи во вращательное движение кулисы и кулисного рычага. Такие передачи являются высокоточными передачами при ограниченных угловых перемещениях (в диапазоне углов до 5⁰), в силу высокого качества изготовления (простых по форме) контактных элементов подвижных звеньев.

Требования к повышению точности прецизионных приборов и преобразователей обусловили необходимость аналитической оценки схемной (теоретической) погрешности измерительного механизма. В данной статье описываются простые по функциональному назначению рычажные передачи, которые для расширения эксплуатационных возможностей прибора объединяются в составные множительные передачи. Приборы, оснащаемые рычажными механизмами, используются в измерительных устройствах станков, переналаживаемых комплексов для контроля предельных отклонений размеров деталей и отклонений формы инструментов.

С практической точки зрения, эффективными оказываются механизмы, обеспечивающие составной контроль отклонений размера и отклонений формы изделия. Подобные измерительные устройства должны иметь, с одной стороны, соответствующие диапазоны измерений, а, с другой стороны, должны отвечать требуемой точности. Теоретическая (схемная) погрешность рычажно-зубчатого механизма является частью предела основной допускаемой погрешности измерительного прибора в целом. В зависимости от величины допускаемой теоретической погрешности производится предварительный схемный анализ и выбор соответствующего вида рычажного механизма. Иными словами, задача анализа точности и синтеза включает выбор структурной схемы механизма и расчет параметров его звеньев, которые позволяют обеспечить требуемую теоретическую погрешность.

Здесь задача обеспечения требуемой точности будет рассматриваться с помощью частных и идеальных функций положения [2,3]. В общем виде теоретическая погрешность определяется разностью функций положения реального и идеального механизмов

x, g, g,…, g) – . (1)

Функция положения , реализующая связь между перемещениями ведущего и ведомого звеньев, зависит от координаты x и размерных параметров g, g₂,…, g подвижных звеньев. Функция зависит от номинальных значений постоянных параметров A_i множительной цепи и воспроизводит теоретическую функцию положения идеального механизма.

На входе рычажного механизма в большинстве случаев используется синусный механизм (с фиксированной длиной синусного рычага). В качестве входного механизма может также использоваться механизм с кулисным входным рычагом. Однако влияние перекосов в поступательной паре и эксцентриситетов во вращательной паре проявляется в синусном механизме значительно меньше. Такие механизмы работают по симметричной схеме расположения пределов измерения от нулевого положения. Зубчатый механизм прибора для линейных измерений устанавливается на выходе измерительной цепи и имеет наименьший коэффициент влияния. Зубчатый механизм воспроизводит линейную зависимость между перемещениями звеньев и не имеет теоретической погрешности.

Вследствие значительных погрешностей изготовления зубчатых пар погрешность оснащаемых ими приборов может устанавливаться в пределах 0,01 мм и более. Поэтому в рычажно-зубчатых измерительных приборах зубчатые передачи устанавливаются предельно близко к отсчетному устройству или сами содержат элементы отсчетного устройства. Благодаря этому однооборотные зубчатые механизмы позволяют проектировать измерительные приборы высокой точности (с погрешностью 0,0005 мм).

Количественная оценка теоретической погрешности является наиболее сложной и наиболее необходимой процедурой, позволяющей аналитическим путем определить ресурс повышения точности и эффективности использования рычажно-зубчатых механизмов [2,3].

Исследуем теоретическую погрешность и её компоненты на примере рычажного синусно-кулисного механизма, относящегося к механизмам с ведущей внутренней кулисой. Частная функция положения рычажного симметричного механизма имеет вид

= arcsin – arcsin . (2)

Зависимость углового выходного перемещения кулисного рычага также может быть выражена в виде отрезка степенного ряда

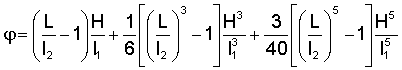. (3)

Принимая, например, z = 228; z = 16 в качестве параметров зубчатой передачи и длину стрелки R = 22 мм, определим передаточное отношение i, связывающее линейное перемещение стрелки с угловым перемещением кулисного рычага (l) 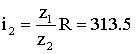. (4)

Общая функция положения механизма примет вид

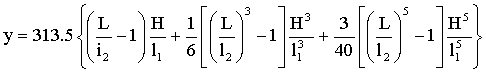. (5)

В рассматриваемом случае измеряемое значение H изменяется от – 140 до + 140 мкм. Теоретическая погрешность схемы определяется разностью функций, выражающих законы движения реального и идеального механизмов

, (6)

где – номинальное передаточное отношение, равное 470 при цене деления 2мкм и интервале деления 0.94мм.

Подставив в (6) найденные выражения получим

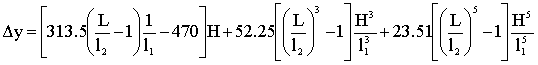. (7)

Номинальные значения параметров схемы l, l, L, z, z, R, входное измеряемое перемещение H, в конечном итоге, определяют величину теоретической погрешности рассматриваемого рычажно-зубчатого измерительного механизма. Все члены разложения частной функции в степенной ряд (3) имеют знак (+), так как отношение параметров реального механизма всегда больше 1.

С учетом этого обстоятельства и принимая во внимание основные свойства функции положения, касающиеся её симметричности, нечетности, диапазона изменения аргумента – 1 x + 1, устанавливаем, что наилучшее равномерное приближение может осуществляться только с помощью полинома Чебышева третьей степени

T₃ (x) = 4x - 3x. (8)

Значения некоторых параметров исследуемого механизма определим, исходя из условия наилучшего равномерного приближения гладкой функции многочленом фиксированной степени, когда в качестве узлов интерполяции используются корни многочлена Чебышева. Задаваясь величинами параметров l = 5 мм, L = 27,54 мм и приравняв коэффициенты полинома Чебышева (8) к коэффициентам соответствующих степеней (7) с заменой переменной x на H = 0.14 мм, получим величину радиуса синусного механизма l = 3.01 мм, исходя из минимума теоретической погрешности.

Рассмотрим частную функцию положения рычажного измерительного механизма с ведущей внешней кулисой

= arcsin + arcsin . (9)

Разложение функции положения в виде отрезка степенного ряда имеет вид

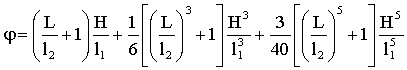. (10)

Задача синтеза элементов средств линейных измерений решается в процессе проведения аналитических и экспериментальных исследований, направленных на снижение или исключение теоретической погрешности. Процедуры, связанные с достижением требуемой точности измерительных приборов и преобразователей контактного типа, сводятся к необходимости проведения синтеза элементов измерительных механизмов. Элементный синтез множительных передач механизмов реализуется с помощью соответствующих функций положения.

Повышение точности многорычажных измерительных механизмов базируется на принципе рационального комбинирования составом различных структурных элементов. Измерительную цепь устанавливают так, чтобы максимально скомпенсировать теоретическую погрешность различных по структурному типу составляющих передач. Пусть функция φ(x) = B(x), описывающая линейную зависимость входной величины x симметричного механизма, аппроксимирована многочленом седьмой степени

φ = Bx + Bx + Bx + Bx,

где B, B, B, B– коэффициенты, зависящие от параметров звеньев механизма. Тогда теоретическая погрешность φ механизма определяется из выражения

φ = B₃x³ + B₅x⁵ + B₇x⁷ . (11)

В известных средствах универсального и активного контактного контроля применяют одноступенчатый измерительный механизм выпускаемых в настоящее время индикаторных рычажно-зубчатых головок 1ИГ и 2ИГ с ценой деления 1мкм и 2мкм соответственно. Перечисленные рычажные и зубчатые механизмы, используемые в измерительных головках или рычажные механизмы, применяемые в индикаторах контакта, отличаются только конструкцией отсчетного устройства.

Проведем схемный анализ симметричных рычажных механизмов (рис. 3, 4) с точки зрения перспективности их использования для средств контактного контроля с расширенными пределами измерения и с фиксированными требованиями к точности.

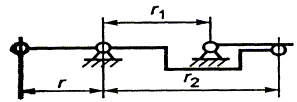
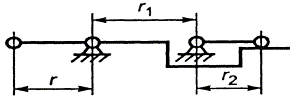
Рис.3. Механизм с ведущим внешним кулисным рычагом	Рис.4. Механизм с ведущей внешней кулисой

Известно, что функция положения рычажного механизма может быть заменена многочленом третьей степени

φ = Bx + Bx.

Погрешность нелинейности рычажной передачи будет определяться членом разложения Bx. Проанализируем поведение функции Bx при одновременном изменении схемных параметров плоского рычажного механизма, сохраняя при этом постоянным общее передаточное отношение.

Принимая во внимание тот факт, что коэффициенты B и B зависят от линейных параметров рычажных механизмов, задача нахождения их оптимальных значений сводится к минимизации члена Bx при условии сохранения общего передаточного отношения рычажной передачи.

Разложение в степенной ряд частной функции положения рычажного механизма (рис. 3) записываются в виде

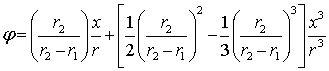, (12)

Степенной ряд функции положения рычажного механизма (рис. 4) имеет вид

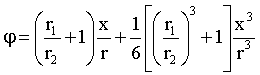, (13)

где – длина синусного рычага; – расстояние между опорами механизма; – длина кулисного рычага. Из выражений (12) и (13) можно получить аналитическое соотношение , выразив функцию через параметр кулисных передач, представленных на рис. 3 и 4. Изменение значений производится при условии B = /r = const. Графические зависимости для механизма с ведущим внешним кулисным рычагом (рис. 3) и механизма с ведущей внешней кулисой (рис. 4) представлены на рис. 5.

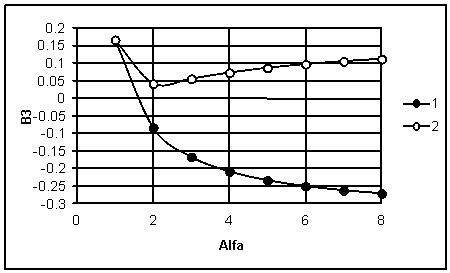
2

1

Рис. 5. 3ависимость коэффициента B от параметра :

1 – для механизма с ведущим внешним кулисным рычагом;

2 – для механизма с ведущей внешней кулисой

Анализ кривых 1 и 2 (рис. 5) показывает, что синтезируемый кулисный механизм (рис. 4), который воспроизводит функцию положения (13), является предпочтительным по условию повышения точности для использования в средствах измерений контактного типа.

Литература:

1. Бундур М.С. Повышение эксплуатационно - технических характеристик технологического оборудования/ М.С. Бундур, В.А. Прокопенко, Н.А.Пелевин// Научно – технические ведомости. – 2012 - № 4.- С.121-127.

2. Лисин, С.К. Средства измерений и контроля линейно-угловых величин: учеб. пособие/ С.К. Лисин.– СПб.: Изд-во СЗТУ, 2010. - 116 с.

3. Лисин, С.К. Теория и средства измерений /С.К. Лисин, А.И. Федотов. – СПб.: Изд-во Политех. ун-та, 2010. – 260 с.

4. Лисин, С.К. Технические измерения /С.К. Лисин, А.И. Федотов. – СПб.: Изд-во НМСУ «Горный», 2012. – 66 с.