К.ф.-м.н. Долгарев И.А.

ЯВНО ЗАДАННАЯ ПОВЕРХНОСТЬ

3-МЕРНОГО ПРОСТРАНСТВА-ВРЕМЕНИ ГАЛИЛЕЯ

Поверхность 3-мерного пространства-времени Галилея, заданная явной функцией, однозначно определяется метрической функцией и двумя коэффициентами ее второй квадратичной формы.

Геометрия 3-мерного коммутативного пространства-времени Галилея изучается в [1] наряду с некоммутативными геометриями галилеевых пространств той же размерности. Основная теорема теории поверхностей пространства-времени Галилея доказана в [2] – это аналог теоремы Петерсона - Бонне евклидовой геометрии. Ниже рассматривается явное задание поверхности пространства Галилея и доказывается основная теорема для этого случая. Доказательство более простое, чем в общем случае.

1. Пространство-время Галилея размерности 3

Пространство событий размерности 3 обозначается и является пространством-временем Галилея. Каждое событие происходит в некоторый момент времени и имеет пространственные координаты в некоторой плоской системе отсчета. Событие записывается в виде . Паре событий и соответствует вектор

.

Все векторы составляют галилеево векторное пространство . Над векторами производятся обычные операции сложения и умножения на действительные числа. Если , и , то

= + = ,

= ;

есть множество действительных чисел.

Пространство-время Галилея относится к пространствам с квазискалярным произведением векторов, в данном случае – галилеевым скалярным произведением векторов. Пусть действительное аффинное пространство, его линейное пространство. В линейном пространстве определено галилеево скалярное произведение векторов и , обозначаемое и равное

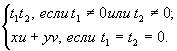= (1)

Галилеево скалярное произведение векторов определено в [1, c. 32-35]. Евклидово скалярное произведение векторов и определяется равенством

= .

Таким образом, для векторов и в равенствах (1) определено евклидово скалярное произведение. На основании (1) вектор , , называется галилеевым, а вектор называется

евклидовым. Векторы

составляют базис Б линейного пространства , и базисом пространства ; . Имеется однозначное разложение вектора в базисе Б:

= , .

Составляющая вектора называется временной, составляющая называется пространственной. Оболочку вектора обозначаем , оболочку обозначаем . Векторные подпространства и пространства являются, соответственно, 1-мерным и 2-мерным евклидовыми векторными пространствами; галилеево векторное пространство есть прямая сумма евклидовых пространств:

= ,

компоненты прямой суммы связаны галилеевым скалярным произведением (1). – временная составляющая, – пространственная составляющая.

По (1) получаем Галилеев скалярный квадрат вектора

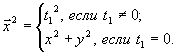
Галилеевой нормой (длиной, модулем) вектора называется :

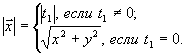(2)

Для векторов галилеева пространства неравенство треугольника на выполняется. Например, если , то ; . Имеем: .

Векторы и называются перпендикулярными, если их скалярное произведение равно нулю, т.е. = 0. Для всякого галилеева вектора и всякого евклидова вектора по (1) выполняется

.

Следовательно, всякий Галилеев вектор перпендикулярен всякому евклидовому вектору. Так как временная составляющая галилеева векторного пространства 1-мерна, то различные два галилеевых вектора могут задавать одно и тоже временное направление. Время течет из прошлого в будущее, имеет два направления – в прошлое и в будущее. Галилеевы векторы и задают одно и тоже направление, если их временные компоненты имеют один и тот же знак: положительный или отрицательный.

В результате определения галилеева скалярного произведения векторов в линейном пространстве аффинного пространства , аффинное пространство превращается в пространство-время Галилея . Точки аффинного пространства становятся точками пространства-времени Галилея, они называются еще событиями. События вида являются временными и составляют в временную компоненту, обозначаемую ; события вида являются пространственными и составляют в пространственную компоненту – евклидову плоскость . Пространство-время Галилея есть прямая сумма оси времени и евклидовой плоскости :

= .

Два события и одновременны, если соответствующий им вектор евклидов, т.е. : временные компоненты событий и совпадают. События и не одновременны, если их временные компоненты различны, т.е. вектор Галилеев. Множество всех событий пространства-времени Галилея обладают тем свойством, что векторы, соответствующие каждой паре событий из этого множества, являются евклидовыми. Согласно галилеевой норме векторов (2), эти события составляют 2-мерное евклидово подпространство пространства-времени Галилея . Таким образом, множество всех одновременных между собой событий является евклидовой плоскостью пространства-времени Галилея. Это пространственные (пространственноподбные) плоскости пространства-времени Галилея. Через каждую точку пространства-времени Галилея проходит единственная евклидова плоскость. Все евклидовы плоскости Галилея параллельны между собою.

Всякий Галилеев вектор определяет в галилееву прямую. Через точку и вектор проходит единственная галилеева прямая в направлении вектора : . Аффинная прямая из является галилеевой прямой в . Точка и евклидов вектор определяют в евклидову прямую. Уравнения прямых в линейны.

Галилеев вектор и евклидов вектор вместе с точкой-событием определяют в галилееву плоскость .

Все галиллевы векторы , временные компоненты которых имеют один и тот же знак, определяют в временное направление, оно совпадает с полупространством в , границей которого является евклидова плоскость. По одну сторону от евклидовой плоскости время течет в одном направлении, по другую сторону – в противоположном. Не существует угла между галилеевыми направлениями, так как время 1-мерно.

Галилеево расстояние между событиями и определяется равенствами

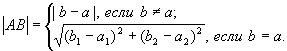(3)

если события и не одновременны, то это есть интервал времени между событиями, длительность события . Если события и одновременны, то есть пространственное расстояние – протяженность события .

2. Поверхности пространства-времени Галилея

Событие, зависящее от времени и пространственного параметра , описывается векторной функцией

, . (4)

Функция задает в поверхность. Поверхности 3-мерного пространства-времени Галилея изучаются в [1]. Дифференцируются галилеевы векторные функции покомпонентно, см. [1]. Считаем, что поверхность регулярна класса . Параметризация (4) поверхности называется естественной. Записываем поверхность в виде временной и пространственной составляющих

= +, (5)

где единичный вектор направления времени, = есть вектор евклидовой плоскости пространства-времени Галилея , это векторное поле на области евклидовой плоскости. Первая квадратичная форма поверхности (4) имеет вид

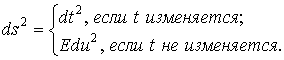(6)

коэффициент есть

, (7)

это метрическая функция поверхности (4), форма (6) имеет тот же вид (2) для галилеевых расстояний. Единичный евклидов вектор нормали равен

. (8)

Вектор перпендикулярен евклидову вектору касательной линии поверхности (4) и галилееву вектору касательной линии поверхности, вектор , согласно (2), является единичным. В каждой обыкновенной точке поверхности существует касательная плоскость , она является галилеевой плоскостью. Все это означает, что рассматриваемая поверхность (4) имеет только галилеевы касательные плоскости и не имеет евклидовых касательных плоскостей, т.к. вектор касательной не является евклидовым. Вторая квадратичная форма поверхности (4) такова

, (9)

ее коэффициенты вычисляются по формулам

(10)

как скалярные произведения евклидовых векторов. В [3] по формулам (7), (8) и (10) составлена система уравнений с частными производными

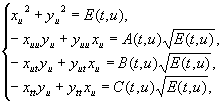(11)

решением которой являются функции – пространственные компоненты функции (4), определяющей поверхность пространства-времени Галилея по заданным функциям (7), (10), – коэффициентам первой и второй квадратичных форм поверхности. При начальных условиях, задающих точку поверхности и неколлинеарные векторы касательной плоскости, поверхность определяется однозначно. Тем самым устанавливается аналог теоремы Петерсона-Бонне.

3. Явно заданная поверхность

Пусть теперь поверхность пространства-времени Галилея задана явной скалярной функцией , . Рассматриваем эту поверхность в векторном задании

= . (12)

По известным коэффициентам (7) и (10) квадратичных форм (6) и (9) поверхности (12) и начальным условиям указанного выше вида, согласно [2], поверхность (12) определяется однозначно. Рассмотрим другую схему (по сравнению с [2]) нахождения поверхности (12). В обозначениях (5) поверхность (12) имеет вид

= +, = . (13)

Частные производные функции (12) таковы: , и

, . (14)

По (7) и (8) имеем соответственно

. (15)

Находим частные производные второго порядка на основе функций (14):

, , . (16)

Согласно (10) и (15), коэффициенты второй квадратичной формы поверхности (12) равны

, , . (17)

По первым формулам в (15) и (17) имеем:

, , . (18)

Следовательно, для получения поверхности достаточно задать метрическую функцию поверхности и коэффициенты ее второй квадратичной формы. По (15) и (17) составляем, как и (11), систему дифференциальных уравнений с частными производными

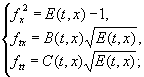(19)

решение этой системы уравнений есть функция , удовлетворяющая указанным выше начальным условиям, определяющая поверхность пространства-времени Галилея однозначно. Начальные условия приобретают вид

. (20)

Система уравнений (11) в рассматриваемом случае принимает вид (19).

Теорема 1. Решение системы уравнений с частными производными (19), удовлетворяющее начальным условиям (20), однозначно определяет поверхность пространства-времени Галилея , описываемую явной функцией , по заданной метрической функции и двум коэффициентам второй квадратичной формы поверхности.

# Второе и третье уравнения системы (19) перепишем в виде

, ;

функция является решением уравнения с полным дифференциалом

. (21)

Заданные функции , удовлетворяют условию

, (22)

так как по (17): . Полученное решение и функция , см. первое уравнение системы (19), определяют функцию как решение уравнения с полным дифференциалом

. (23)

Единственная функция выделяется начальными условиями (20). #

Решение системы уравнений с частными производными (19) сведено к последовательному решению двух уравнений с полным дифференциалом (21) и (22).

Согласно доказательству теоремы 1, коэффициенты квадратичных форм поверхности (12) удовлетворяют условиям (21) и тому, что (22) есть уравнение с полным дифференциалом. Второе из условий принимает еще форму, учитывающую значение производной , см. (18), и то, что . Таким образом, второе условие есть

. (24)

Теперь, задавая функции

, (25)

нужно учитывать (22) и (24). Выполняется следующая теорема.

Теорема 2. Если заданы функции (25), удовлетворяющие условиям (22) и (24) и начальные условия (20), то решение системы дифференциальных уравнений с частными производными (19) однозначно определяет поверхность пространства-времени Галилея, описываемую явной функцией , а, значит, и векторной функцией (12); коэффициенты квадратичных форм этой поверхности совпадают с (25). #

Пример 1. Найдем поверхность пространства-времени Галилея по заданным коэффициентам ее квадратичных форм: .

Согласно (15), получаем: . Условие (19) выполняется, уравнение (18) имеет вид

,

его решение: . Теперь получим уравнение вида (20). Так как , то уравнение (20) конкретизируется в виде

.

Решение этого уравнения есть 2-параметрическое семейство поверхностей

.

Начальные условия выделяют поверхности

.

Полученные функции определяют параболоиды – эллиптический и гиперболический.

Пример 2. Даны функции

; .

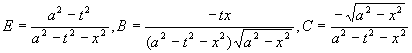В пространстве-времени Галилея укажем поверхность, метрическая функция которой совпадает с данной функцией , коэффициенты второй квадратичной формы которой есть и которая проходит через точку , касаясь плоскости .

Для заданных функций выполняется условие (22), т. е. имеется уравнение с полным дифференциалом вида (21). Находим:

.

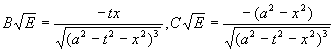При сокращении уравнения

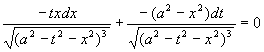
на ненулевой множитель получаем , а это выражение не является полным дифференциалом никакой функции. Для функций и имеем

== .

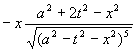Условие (22) выполняется. Решением уравнения является функция

.

По заданному уравнению касательной плоскости имеем , следовательно, . Из условия находим

и проверка показывает, что справедливо условие (24): . Решением уравнения с полным дифференциалом

при начальных условиях является функция

.

Тем самым решена система дифференциальных уравнений с частными производными (19), коэффициенты ее есть заданные функции , и удовлетворяются начальные условия . Схема решения этой системы уравнений совпадает с изложенной в доказательстве теоремы 1. Мы получили параметрическое задание поверхности

,

проходящей через точку и касающуюся плоскости в точке . Полученная поверхность есть верхняя полусфера .

Список литературы.

1. Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

2. Долгарев И.А. Нахождение поверхности в пространстве Галилея по ее квадратичным формам. // Известия высших учебных заведений. Поволжский регион. – 2006, № 5(26), С. 51 – 60. - (Естественные науки).

3. Долгарев И.А. Системы дифференциальных уравнений в частных производных для поверхностей пространства Галилея: дис. … канд. физ.-мат. наук - Пенза: ПГУ, 2007. – 119с.