М. П. Ленюк
Чернівецький факультет НТУ”ХПІ”
Скінченне гібридне
інтегральне перетворення типу
Фур’є – Бесселя - Лежандра на сегменті [R0,R3] полярної осі
Побудуємо на множині ![]() інтегральне перетворення, породжене гібридним диференціальним
оператором (ГДО).
інтегральне перетворення, породжене гібридним диференціальним
оператором (ГДО).
![]() (1)
(1)
У рівності (1) ![]() - одинична функція Гевісайда [1],
- одинична функція Гевісайда [1], ![]() -диференціальний оператор Фур’є другого порядку [2],
-диференціальний оператор Фур’є другого порядку [2], ![]() - диференціальний оператор Бесселя [3],
- диференціальний оператор Бесселя [3], ![]() - узагальнений диференціальний
оператор Лежандра [4]:
- узагальнений диференціальний
оператор Лежандра [4]:
![]()
![]()
Означення: Областю задання
ГДО ![]() назвемо множину G вектор-функцій
назвемо множину G вектор-функцій ![]() з такими властивостями:
з такими властивостями:
1)
вектор-функція ![]() неперервна на
неперервна на ![]() ;
;
2)
функції ![]() задовольняють крайові
умови
задовольняють крайові
умови
![]() (2)
(2)
3)
функції ![]() задовольняють умови
спряження
задовольняють умови
спряження ![]()
![]() (3)
(3)
Умови на коефіцієнти: ![]()
![]()
Визначимо числа
![]()
вагову функцію
![]() (4)
(4)
та скалярний добуток
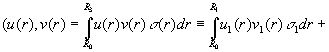
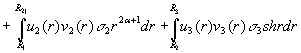 (5)
(5)
Зауважимо, що із умов спряження
(3) випливає базова тотожність: для ![]() та
та ![]() має місце тотожність
має місце тотожність
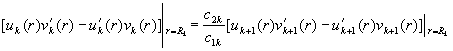 (6)
(6)
Покажемо, що ГДО ![]() самоспряжений. Згідно
правила (5) для
самоспряжений. Згідно
правила (5) для ![]() та
та ![]()
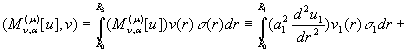
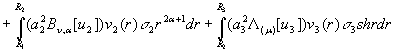 (7)
(7)
Проінтегруємо в (7) під знаком інтегралів два рази частинами:
![]()
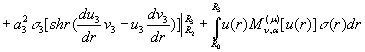 (8)
(8)
Якщо
![]() то в силу крайової
умови в точці
то в силу крайової
умови в точці ![]() маємо:
маємо:
![]()
![]()
![]() (9)
(9)
Якщо ![]() то в силу крайової
умови в точці
то в силу крайової
умови в точці ![]() маємо:
маємо:
![]()
![]() (10)
(10)
В силу базової тотожності (6) в
точці ![]() знаходимо, що
знаходимо, що
![]()
![]() (11)
(11)
тому, що
внаслідок вибору чисел ![]() та
та ![]() вираз
вираз
![]()
В силу базової тотожності (6) в
точці ![]() знаходимо, що
знаходимо, що
![]()
![]() (12)
(12)
тому, що
внаслідок вибору чисел ![]() та
та ![]() вираз
вираз
![]()
В
силу рівностей (9)-(12) у формулі (8) позаінтегральні вирази
рівні нулю і ми одержуємо рівність
![]() (13)
(13)
Рівність
(13) показує, що ГДО ![]() самоспряжений. Звідси випливає, що
його спектр дійсний. Оскільки ГДО
самоспряжений. Звідси випливає, що
його спектр дійсний. Оскільки ГДО ![]() на множині
на множині ![]() немає особливих
точок, то його спектр дискретний [5]. Йому відповідає дійсна
спектральна функція. Власні елементи ГДО
немає особливих
точок, то його спектр дискретний [5]. Йому відповідає дійсна
спектральна функція. Власні елементи ГДО ![]() ( власні числа й відповідні їм
власні функції) знайдемо як ненульовий розв’язок відповідної спектральної задачі Штурма-Ліувілля.
( власні числа й відповідні їм
власні функції) знайдемо як ненульовий розв’язок відповідної спектральної задачі Штурма-Ліувілля.
Нехай
![]() -спектральний параметр, а функції
-спектральний параметр, а функції ![]() - компоненти спектральної вектор-функції
- компоненти спектральної вектор-функції
![]() (14)
(14)
Розглянемо
регулярну спектральну задачу Штурма-Ліувілля: знайти не нульовий розв’язок
сепаратної системи звичайних диференціальних рівнянь Фур’є, Бесселя та Лежандра
![]()
![]() (15)
(15)
![]()
за однорідними крайовими умовами
![]() (16)
(16)
та однорідними умовами спряження
![]() (17)
(17)
Фундаментальну
систему розв’язків для диференціального рівняння Фур’є ![]() утворюють функції
утворюють функції ![]() та
та ![]() [2]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя
[2]; фундаментальну
систему розв’язків для диференціального рівняння Бесселя ![]() утворюють функції
Бесселя
утворюють функції
Бесселя ![]() та
та ![]() [3];
фундаментальну систему розв’язків для диференціального рівняння Лежандра
утворюють функції
[3];
фундаментальну систему розв’язків для диференціального рівняння Лежандра
утворюють функції ![]() та
та ![]() [4];
[4];
![]()
Лінійність
спектральної задачі Штурма-Ліувілля (15)-(17) дозволяє покласти
![]()
![]()
![]() (18)
(18)
![]()
Крайові умови (16) та умови спряження (17)
для визначення шести величин ![]() дають однорідну
алгебраїчну систему із шести рівнянь:
дають однорідну
алгебраїчну систему із шести рівнянь:
![]()
![]()
![]() (19)
(19)
![]()
Введемо
до розгляду функції
![]()
![]()
![]()
![]()
![]()
Алгебраїчна
система (19) має відмінний від нуля розв’язок тоді й тільки тоді, коли її
визначник рівний нулю [6]:
![]()
![]() (20)
(20)
Ми
одержали трансцендентне рівняння для обчислення власних чисел ГДО ![]() .
.
Згідно з роботою [7] маємо
твердження.
Теорема
1 (про
дискретний спектр). Корені ![]() трансцендентного
рівняння
трансцендентного
рівняння ![]() складають дискретний
спектр ГДО
складають дискретний
спектр ГДО ![]() : дійсні, різні, симетричні відносно
: дійсні, різні, симетричні відносно ![]() й на півосі
й на півосі ![]() утворюють монотонну
зростаючу числову послідовність з єдиною точкою згущення
утворюють монотонну
зростаючу числову послідовність з єдиною точкою згущення ![]() .
.
Підставимо
в алгебраїчну систему (19) ![]() й відкинемо останнє рівняння в силу лінійної залежності.
й відкинемо останнє рівняння в силу лінійної залежності.
Припустимо, що ![]() , де
, де ![]() підлягає визначенню.
Тоді перше рівняння системи перетворюється в тотожню рівність, а наступні два
рівняння дають алгебраїчну систему з двох рівнянь для визначення величин
підлягає визначенню.
Тоді перше рівняння системи перетворюється в тотожню рівність, а наступні два
рівняння дають алгебраїчну систему з двох рівнянь для визначення величин ![]()
![]() (21)
(21)
Визначник алгебраїчної системи (21) обчислюється
безпосередньо:
![]() .
.
Алгебраїчна система (21) має єдиний розв’язок [6]:
![]()
![]() (22)
(22)
При відомих ![]() для визначення
для визначення ![]() маємо алгебраїчну систему з двох
рівнянь:
маємо алгебраїчну систему з двох
рівнянь:
![]() (23)
(23)
Визначник алгебраїчної системи (23) обчислюється
безпосередньо:![]()
![]()
![]()
Алгебраїчна
система (23) має єдиний розв’язок [6]:
![]() (24)
(24)
![]()
Підставимо
визначені за правилами (22) та (24) величини ![]() у формули (18).
Отримуємо функції:
у формули (18).
Отримуємо функції:
![]()
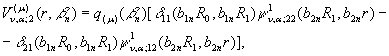 (25)
(25)
![]()
![]()
Згідно рівності (14) спектральна
вектор-функція ![]() визначена. При цьому її квадрат норми
визначена. При цьому її квадрат норми
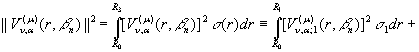
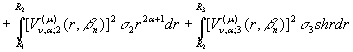 (26)
(26)
Згідно
з роботою [7] сформулюємо твердження.
Теорема
2
(про дискретну функцію). Система власних функцій ![]()
ортогональна на множині ![]() з ваговою функцією
з ваговою функцією ![]() , повна й замкнена.
, повна й замкнена.
Теорема
3
(про зображення рядом Фур’є). Будь-яка вектор-функція ![]() зображається за
системою
зображається за
системою ![]() абсолютно й
рівномірно збіжним на множині
абсолютно й
рівномірно збіжним на множині ![]() рядом Фур’є:
рядом Фур’є:
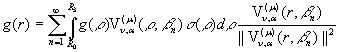 (27)
(27)
У системі ортонормованих власних функцій
![]()
![]()
ряд Фур’є (27) набуває вигляду
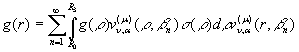 (28)
(28)
Ряд Фур’є (28) визначає пряме ![]() й обернене
й обернене ![]() скінченне гібридне інтегральне перетворення (СГІП), породжене на множині
скінченне гібридне інтегральне перетворення (СГІП), породжене на множині ![]() ГДО
ГДО ![]() :
:
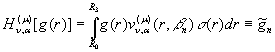 (29)
(29)
![]()
![]() (30)
(30)
Визначимо
величини та функції:
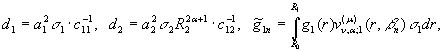
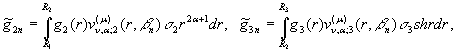
![]()
Теорема 4 (про основну тотожність). Якщо вектор-функція ![]() неперервна на множині
неперервна на множині
![]() , а функції
, а функції ![]() задовольняють крайові
умови
задовольняють крайові
умови
![]() (31)
(31)
та умови
спряження
![]() (32)
(32)
то має місце основна тотожність СГІП ГДО ![]() :
:
![]()
![]() (33)
(33)
Доведення: За правилом (29)
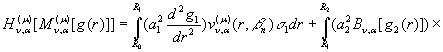
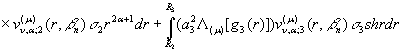 (34)
(34)
Проінтегруємо під знаками інтегралів два рази
частинами:
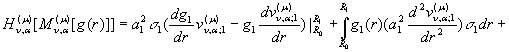
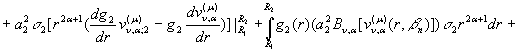
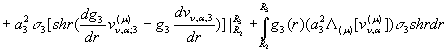 (35)
(35)
Якщо ![]() , то
, то
![]()
![]()
![]() (36)
(36)
Якщо ![]() , то
, то
![]()
![]()
![]() (37)
(37)
Скористаємося базовою тотожністю
для випадку, коли умови спряження неоднорідні:
![]()
![]() (38)
(38)
При ![]() в точці спряження
в точці спряження ![]() знаходимо, що
знаходимо, що
![]()
![]()
![]() (39)
(39)
тому, що в силу вибору чисел ![]() та
та ![]() вираз
вираз
![]()
При ![]() в точці спряження
в точці спряження ![]() знаходимо, що
знаходимо, що
![]()
![]()
![]() (40)
(40)
тому, що в силу вибору чисел ![]() та
та ![]() вираз
вираз
![]()
Із диференціальних тотожностей
![]()
![]()
![]()
знаходимо диференціальні рівності
![]()
![]() (41)
(41)
Якщо в рівності (35) підставити функціональні
співвідношення (36)-(41), то будемо мати:
![]()
![]() (42)
(42)
Оскільки
![]() ,
,
то одержана тотожність (42) співпадає з тотожністю
(33).
Доведення
теореми завершено.
Одержані
правила (29), (30) та (33) складають математичний апарат для одержання
інтегрального зображення аналітичного розв’язку відповідних задач математичної
фізики неоднорідного середовища.
Список
використаної літератури:
1. Шилов Г.Е. Математический
анализ. Второй специальний курс. – М.: Наука, 1965. –
328с.
2. Степанов В.В. Курс дифференциальних уравнений. – М.: Физматгиз, 1959. – 468с.
3. Ленюк М.П. Исследования основных краевых задач для диссипативного волнового
уравнения Бесселя. - Киев, 1983. – 62с.
– (Препринт / АН УССР. Ин-т математики; 83.3).
4. Конет І.М., Ленюк М.П.
Інтегральні перетворення типу
Мелера-Фока. – Чернівці: Прут, 2002. – 248с.
5. Ленюк М.П., Шинкарик М.І.
Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина 1. –
Тернопіль: Економічна думка,
2004. – 368с.
6. Курош А.Г. Курс высшей алгебры.
– М.: Наука, 1971. – 432с.
7. Комаров Г.М., Ленюк М.П.,
Мороз В.В. Скінченні гібридні інтегральні перетворення, породжені
диференціальними рівняннями другого порядку. - Чернівці: Прут, 2001. – 228с.