УДК 539.376

А.Г. ТАМРАЗЯН, д-р техн. наук, академик РИА, профессор (МГСУ), (Россия)

Д.Г. КЛЕКЧЯН, канд. техн. наук (ЕАСГУ), (Республика Армения)

Особенности расчета железобетонных элементов с учетом ползучести и старения бетона

Напряженно-деформированное состояние железобетонных элементов и конструкций со временем из-за ползучести и старения неизменно меняется. Эти изменения непосредственно зависят как от меры полазучести , так и от закономерности изменения модуля деформации бетона. Аналитическую зависимость принято представлять по формуле Н.Х. Арутюняна[1,2]:

, (1)

где - опытные параметры. Однако недостаток этой формулы заключается в том, что значение определяется не на базе , которое легко получить непосредственным испытанием в самом начале процесса , а , которое в момент не может быть известным. Поэтому в практических расчетах мы рекомендуем пользоваться формулой

, (2)

которая освобождена от отмеченного недостатка.

Расчет конструкций с учетом ползучести значительно зависит от аналитической функции меры ползучести . Учитывая характер ползучести бетонов, аналитическая функция должна учитывать следующие условия. Влияние возраста бетона при загружении, поскольку, чем моложе бетон при загружении, тем интенсивнее происходит его ползучесть. Длительность загружения . Можно предложить обобщенную формулу меры ползучести

, (3)

где характеризует процесс взросления бетона, а длительность загружения. Вид и должны быть такими, чтобы удовлетворялись следующие условия.

С ростом монотонно растет, но с убывающей скоростью, т.е. при :

. (4)

Это условие означает:

. (5)

– с ростом монотонно убывает с убывающей скоростью, что приводит к неравенствам:

; ; . (6)

Эти условия будут удовлетворены, если

; ; ; и т.д.

Из обобщенной функции (1) соответствующими подстановками можно получить известные в технической литературе[1,2,3] разные аналитические формулы . Так например, чтобы получить меру ползучести теории наследственности[2,3]

, (7)

необходимо в (1) подставить

. (8)

Мера ползучести теории старения[3]

(9)

получится подстановкой

. (10)

Мера ползучести академика Н.Х. Арутюняна[1]

, (11)

требует подстановку

. (12)

Мера ползучести проф. С.Г. Есаяна[3] и требуемая подстановка

(13)

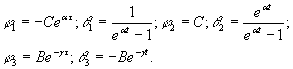(14)

Из эмпирических формул можно привести, например, меру ползучести, предложенную проф. С.В. Александровским[2]:

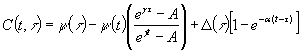, (15)

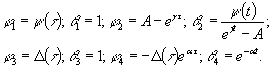(20)

Если действующие в элементе нормальные напряжения со временем сохраняются постоянными, то связь – будет:

. (21)

При переменных нормальных напряжениях связь – выразится интегральным уравнением Вольтерра второго рода:

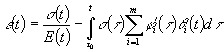. (22)

Введем понятие коэффициента изменения напряжений со временем:

, (23)

где напряжение, приложенное в начальный момент времени :

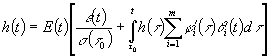. (24)

В интегродифференциальном уравнении (24) входят две неизвестные и . Для решения этого уравнения необходимо иметь уравнение связи. Учитывая условия равновесия и совместности деформаций, получится второе уравнение связи –:

, (25)

где и – постоянные, значения которых в каждом отдельном случае зависят от условий задачи.

Подставив (25) в (23) и учитывая, что при , получим недостающую вторую связь –

, (26)

и тогда (24) превратится в интегральное уравнение для определения

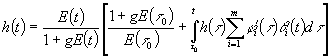. (27)

Решение интегродифференциального уравнения (27) является весьма сложной математической задачей. Значение ищем в виде степенного ряда Тейлора, разложенного по степеням

, (28)

где положительный параметр

. (29)

Входящие в (29) коэффициенты определяются через :

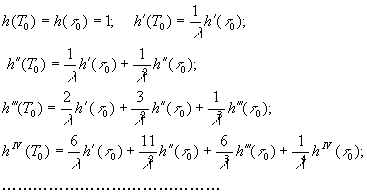(30)

Коэффициенты определяются из исходного интегрального уравнения (27) его поочередным дифференцированием по и подстановкой в полученных выражениях . Например значения и будут

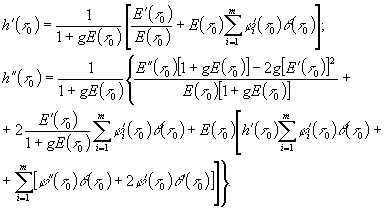(31)

При :

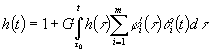. (32)

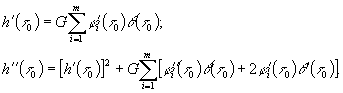(33)

где через обозначено выражение

. (34)

Заметим, что если взять значения параметра по формуле

, (35)

то уже третий член ряда (29) превращается в ноль, что значительно активизирует его сходимость и дает возможность с необходимой точностью получить значение неизвестного , оставив первые два члена ряда (29):

. (36)

Пример. Трубобетонный элемент (с модулем сдвига бетона , и стальной трубы ) начиная с момента времени находится под воздействием постоянного крутящего момента . Требуется определить закономерность изменения со временем касательных напряжений в бетоне вызванное его ползучестью.

Функцию меры ползучести бетона представим, например, по формуле Н.Х. Арутюняна (1). Тогда интегральное уравнение (24) получит вид

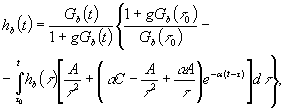. (35)

где , а параметры определены испытанием бетона на ползучесть при сдвиге.

Двойным дифференцированием интегральное уравнение (35) превратится в дифференциальное уравнение второго порядка с переменными коэффициентами

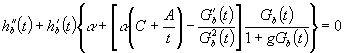(32)

с решением

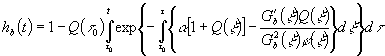, (33)

где введены обозначения

, . (34)

Поскольку требуется определить закономерность изменения , вызванной ползучестью бетона, то принимая получим

, (35)

где

.

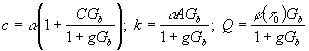Функция

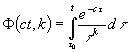(36)

табулированная неполная гамма функция [2].

Учитывая уравнения равновесия и совместности деформаций бетона и металлической трубы, интегральное уравнение для определения будет иметь вид

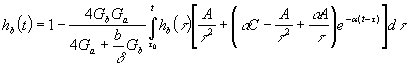, (37)

где –диаметр бетонного цилиндра, –толщина стенки металлической трубы.

Решим числовой пример при следующих данных

см²/кг.сила; см²/кг.сила; день^–1;

; кг.сила/см²; кг.сила/см²; 14день.

Результаты подсчетов при 14, 45, 60, 90, 180, 360, дням по точным и приближенным формулам приведены в таблице.

в днях	45	60	90	180	360
точные значения	0,384	0,328	0,300	0,296	0,296	0,296
приближенные значения	0,370	0,315	0,295	0,293	0,293	0,293

Сравнение точных и приближенных результатов подсчета показывает, что расхождения между ними не превосходит 4%-а, что вполне приемлемо для практических расчетов.

Библиографический список

1. Арутюнян Н.Х. Некоторые вопросы теории ползучести. –М.: Гостехиздат, 1952. –324 с.

2. Александровский С.В. Расчет бетонных и железобетонных конструкций на изменение температуры и влажности с учетом ползучести. –М.: Стройиздат, 1973. –432 с.

3. Есаян С.Г. Реологическое моделирование вязкоупругих, упругопластических и вязкоупругопластических сред.–Ереван, Чартарагет, 209, –368 с.