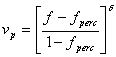Сеничев В.Ю., Терешатов
В.В., Макарова М.А., Волкова Е.Р., Якушев Р.М., Федосеев М.С.
Институт технической
химии Уральского отделения РАН, Пермь, Россия
АНАЛИТИЧЕСКОЕ ОПИСАНИЕ ЗависимостИ напряжение–деформация для
сегментированных эластомеров полиЭФИРуретанового типа
Известно, что эластичные полиуретановые
материалы являются одним из самых ценных материалов, применяемых в самых
различных отраслях техники и медицины [1]. В зависимости от используемых при
синтезе компонентов они представляют собой полиуретаны или полиуретанмочевины.
Полимерные цепи в молекулах этих материалов состоят из чередующихся жестких и
эластичных сегментов. Различие в полярности таких сегментов может вызывать
фазовое разделение с образованием в эластомере дисперсной жесткой фазы, играющей
роль усиливающего нанодисперсного наполнителя. При этом резко повышается модуль
системы, увеличивается прочность, но величина критических деформаций при
растяжении остается на достаточно высоком уровне (300-500%). Такие свойства
двухфазные полиуретановые (и полиуретанмочевинные) эластомеры имеют в широком
диапазоне концентрации жестких сегментов вплоть до появления эффекта резкого
снижения деформативности при достижении концентрации жестких сегментов
определенного порогового значения, выше которого деформация материала идет
частично уже в режиме пластического течения. Обычно такой порог наблюдается при
объемной концентрации жестких сегментов 40-40% объемных. Теоретическое
рассмотрение деформации сегментированных эластомеров представляет собой сложную
задачу, что связано с двойственной природой нанодисперсной фазы. С одной стороны, ее можно рассматривать в
качестве аналога минеральных наполнителей и, таким образом, связывать изменение
характеристик сегментированных эластомеров с объемной долей доменов жестких
блоков (микромеханистическая модель) [2]. В этой модели модуль дается как
функция объемной концентрации жестких сегментов и температуры:
|
|
(1) |
Где
EH -модуль жесткой фазы (авторы
приняли его равным 5 ГПа),
EFS – модуль наполненной мягкой фазы, а vP
–объемная доля эластически активной жесткой фазы, которая определяется
следующим образом:
|
|
(2) |
Здесь
δ– это перколяционная экспонента, а fperc –порог перколяции для
жесткой фазы. Перколяционная экспонента обычно находится между 1.5 и 2.5 в
зависимости от типа системы и того свойства, которое описывает модель
перколяции (модуль, проводимость). Порог перколяции зависит от морфологии
перколяционых кластеров, и таким образом от несовместимости между двумя фазами.
Недостатком данной модели является то, что невозможно численно оценить объемную
долю жесткой фазы в том случае, если имеет место ограниченная совместимость
жестких сегментов и эластичной матрицы,
что характерно для полиуретанов и полиуретанмочевин на основе полиэфиров. С другой стороны, домены жестких блоков можно
также рассматривать в качестве узлов физической сетки, относительно стабильных при невысоких температурах. На наш взгляд, это наиболее
продуктивный подход, ввиду того, что концентрация таких узлов может быть
экспериментально определена независимым путем [3]. Такое рассмотрение позволяет применить к рассмотрению
деформирования сегментированных эластомеров подход, использованный нами ранее
для описания зависимости
напряжение-деформация однофазных эластомеров [4]. Данный
подход учитывает как конечную растяжимость полимерных цепей, так и изменение эластичности на начальной стадии
деформирования эластомера. В рамках данного подхода было выведено уравнение для
зависимости напряжения от деформации при простом растяжении эластомеров,
имеющих сетку с трехфункциональными узлами:
|
|
(3) |
где λ-степень относительного растяжения, a- коэффициент
нерастяжимости цепи, ![]() ,
, ![]() -плотность химической сетки,
-плотность химической сетки,
![]() - структурный параметр (
- структурный параметр (![]() ), который можно отнести к относительной доле цепей,
ориентирующихся при воздействии высоких деформаций; параметры b,d – постоянные для
широкого круга сеток. Величина a может
приблизительно быть сопоставлена с величиной степени относительного растяжения
при разрыве λmax:
), который можно отнести к относительной доле цепей,
ориентирующихся при воздействии высоких деформаций; параметры b,d – постоянные для
широкого круга сеток. Величина a может
приблизительно быть сопоставлена с величиной степени относительного растяжения
при разрыве λmax: ![]() .
Как было установлено, уравнение (3) хорошо описывает зависимости
напряжение-деформация для однофазных эластомеров [4].
.
Как было установлено, уравнение (3) хорошо описывает зависимости
напряжение-деформация для однофазных эластомеров [4].
В рамках настоящей работы были рассмотрены
сегментированные (двухфазные) эластомеры полиуретанового типа на основе простых
и сложных полиэфиров. Простые полиэфируретаны серии BPL (Табл.1) были
изготовлены на основе олиготетраметиленгликоля (полифурит) с молекулярной
массой 1000, олигооксипропилентриола с молекулярной массой 370 (лапрол 373) и
метилен-орто-бис-хлоранилина (MOCA). Предварительно часть
полифурита была использована для получения псевдофорполимера СКУ-М-2.5. При
получении данного продукта мольное соотношение полифурит: дифенилметандиизоцианат
составляло 1:2.5, что обеспечивало заметное содержание в полученном
псевдофорполимере свободного диизоцианата (около 33% мольных). Готовый
псевдофорполимер отверждали смесью полифурита, лапрола 373 и MOCA.
Методика подготовки образцов приведена в работе [4].
Таблица
1 Состав полиуретановых образцов серии BPL на основе простых
полиэфиров (в мольных долях)
|
Образец |
СКУ-М-2.5 |
Полифурит |
Лапрол
373 |
MOCA |
Доля
жестких сегментов, масс. |
|
BPL-1 |
1.08 |
0.95 |
0.05 |
0 |
0 |
|
BPL-2 |
1.08 |
0.85 |
0.05 |
0.1 |
0.03 |
|
BPL-3 |
1.08 |
0.75 |
0.05 |
0.2 |
0.06 |
|
BPL-4 |
1.08 |
0.6 |
0.05 |
0.35 |
0.11 |
Сложные полиэфируретаны серии LBA
(Табл.2) были изготовлены на основе гидроксилсодержащего олигоэфира ОМА-2100 с
молекулярной массой 2000, триметилолпропана (этриол) и MOCA. Олигоэфир ОМА
представляет собой продукт конденсации адипиновой кислоты, диэтиленгликоля и
бутандиола, при равном мольном соотношении олигодиолов между собой. Предварительно
часть олигоэфира ОМА-2100 была использована для получения форполимера СКУ-7ЛБА.
При получении форполимера соотношение олигоэфир: 2,4-толуилендиизоцианат
выдерживалось 1:2.06. Готовый форполимер отверждали смесью ОМА-2100 и MOCA.
Методика подготовки образцов аналогична серии BPL.
Таблица
2 Состав полиуретановых образцов серии LBA на основе сложных
полиэфиров (в мольных долях)
|
Образец |
СКУ-7ЛБА |
ОМА-2100 |
этриол |
MOCA |
Доля
жестких сегментов, масс. |
|
LBA-1 |
1.08
|
0.8 |
0.1 |
0.1 |
0.01 |
|
LBA -2 |
1.08 |
0.6 |
0.1 |
0.3 |
0.04 |
|
LBA -3 |
1.08 |
0.4 |
0.1 |
0.5 |
0.07 |
|
LBA -4 |
1.08 |
0.2 |
0.1 |
0.7 |
0.11 |
У отвержденных образцов была определена
плотность пространственной сетки (Табл.3). Ее значение было установлено с
использованием модуля растяжения образцов, набухших в этилацетате. Как было
показано ранее [3], плотность сетки, определенная с использованием
растворителей, не разрушающих доменную структуру, для сегментированных
эластомеров представляет собой суперпозицию двух сеток: истинной химической
сетки и сетки, узлы которой являются доменами жестких блоков.
|
|
|
|
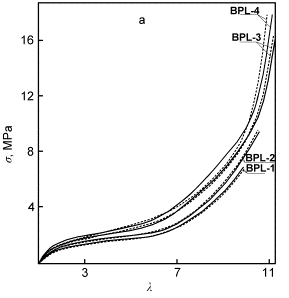
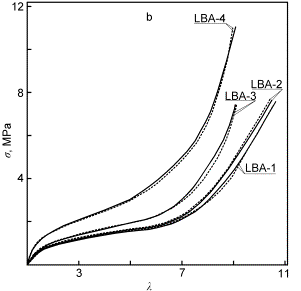
Рис.1.
Зависимость деформация-напряжение для изученных сегментированных
полиэфируретановых эластомеров BPL(a)
и LBA(b). Экспериментальные
зависимости обозначены сплошными линиями, расчет по уравнению (3) - пунктиром. |
|
Таблица
3. Параметры уравнения (3) для исследованных эластомеров
|
Образец |
NC ·104, моль/см3 |
α |
|
a |
d |
|
BPL-1 |
1.44 |
0.08 |
0.15 |
0.5 |
0.2 |
|
BPL-2 |
1.56 |
0.08 |
0.15 |
0.5 |
0.2 |
|
BPL-3 |
1.80 |
0.08 |
0.15 |
0.5 |
0.2 |
|
BPL-4 |
2.16 |
0.08 |
0.15 |
0.5 |
0.2 |
|
LBA-1 |
1.18 |
0.09 |
0.1 |
0.5 |
0.2 |
|
LBA-2 |
1.22 |
0.088 |
0.1 |
0.5 |
0.2 |
|
LBA-3 |
1.48 |
0.095 |
0.1 |
0.5 |
0.2 |
|
LBA-4 |
2.33 |
0.095 |
0.1 |
0.5 |
0.2 |
Величина
параметра d выбрана равной 0.2,
остальные структурные параметры определены, используя программу OriginPro 8.6.0.
На рисунке 1 показаны расчетные и
экспериментальные кривые растяжения. Как видно из графиков, разработанная ранее
авторами модель может успешно использоваться для описания деформационного
поведения сегментированных эластомеров в области невысокого содержания жесткой
фазы без каких-либо корректировок.
Литература
1. Prisacariu, C. Polyurethane elastomers from morphology to mechanical aspects. Springer-Verlag: Wien, NewYork, 2011.
2.
Ginzburg V.V.,
Bicerano J., Christenson C.P., Schrock A.K., Patashinski A.Z. Modeling
Mechanical Properties of segmented Polyurethanes. In Nano- and micromechanics
of polymer blends and composites / edited by Karge-Kocsis J. and Fakirov S.
Munich, Carl Hanser Verlag, 2009.
3.
Tereshatov V.V., Tereshatova E.N.,
Volkova E.R. Two types of physical networks in cross-linked segmented
polyurethanes. Polymer Science. A. V. 37. 1995. 1157-1163.
4.
Tereshatov V.V., Senichev V.Yu. Stress-Strain Dependence of Cross-Linked
Single-Phase Polyether Urethane. J. of Macromolecular Sci. Part B:
Physics.
V.53. P.575-587.