К. ф.-м. н. Махина Н.М.

Брянский государственный университет им. ак. И.Г. Петровского, Россия

Ортогональность некоторых систем функций

в пространствах аналитических функций с весом

Обозначим , – некоторая односвязная область на комплексной плоскости ; функция конформно отображает на , – обратная функция для .

Пусть также – класс кривых таких, что , где , – произвольные точки на кривой, – длина кратчайшей дуги кривой, соединяющей точки (см., например, [1], с. 280); – класс кривых, являющихся гладкими жордановыми всюду, кроме конечного числа точек , в которых кривая образует углы 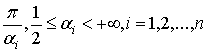(см. [3]).

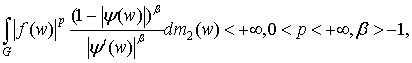Обозначим также – класс измеримых по Лебегу в области функций таких, что где – плоская мера Лебега; – подпространство пространства , состоящее из аналитических функций.

Заметим, что с учетом оценок, следующих из известной теоремы Кебе (см. [1, с. 5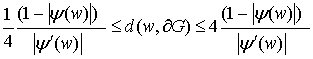1]):

, (1)

пространство в определенном смысле эквивалентно пространству измеримых по Лебегу в области функций таких, что – расстояние от точки до границы области .

В работе [3] для односвязной области , , показано, что система функций 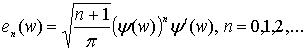, является базисом в пространстве , если при , и если при , где .

В нашей работе мы строим базисы в весовых пространствах функций , , аналитических в областях с границей класса , т.е. в областях Лаврентьева (см., например, [2], [4]). Для этого сначала докажем ортогональность рассматриваемой системы функций.

Теорема. Пусть – односвязная ограниченная область, , функция конформно отображает на , причем – некоторая точка из , , – обратная функция для .

Если , , 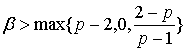то система функций

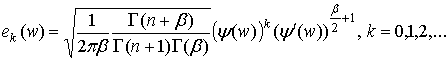, (2)

ортогональна в пространстве .

Доказательство.

Покажем, что система функций (2) является ортогональной в пространстве , то есть

Пусть тогда , используя двойное неравенство, которое выводится из теоремы Кёбе (см. [1, с. 51])

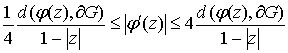, (3)

заметим, что 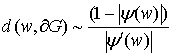, тогда достаточно доказать

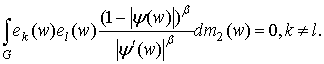
Но .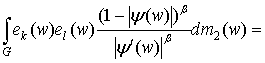

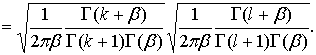
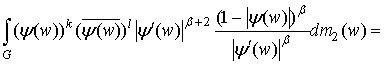
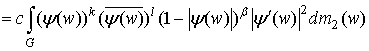Снова переходя к единичному кругу с помощью замены получим: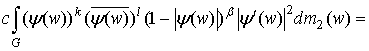

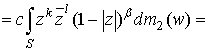
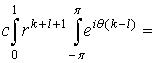0 при .

Итак, данная система ортогональна.

Литература

1. Голузин Г.М. Геометрическая теория функций комплексного переменного / Г.М. Голузин. – М.: Наука, 1966.

2. Привалов И. И. Граничные свойства аналитических функций / И.И. Привалов. – М.-Л.: ГИТТЛ, 1950.

3. Шихватов А.М. Об -пространствах функций, аналитических в области с кусочно-аналитической границей / А.М. Шихватов // Математические заметки. – 1976. – Т. 20, № 4. – С. 537-548.

4. Pommerenke Ch. On univalent functions, Bloch functions and VMOA / Ch. Pommerenke // Math. An. – 1978. – V. 236. – P. 199-208.