Комолов В.М., к. физ.-мат. н. Латынин Ю.М.

                Украинская инженерно-педагогическая академия, г. Харьков

 

 Об эквивалентности ряда формул  плоского косоугольного треугольника

 

          I. В соответствии с теоремой о проекциях [1] для произвольного плоского треугольника со сторонами a,b,c и противолежащими им углами α,β,γ (рис. 1) для определения длины стороны   с  справедливо соотношение:

 

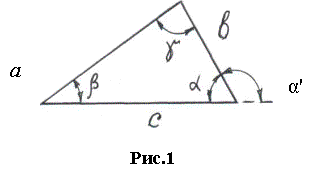                                                c= a∙cosβ +b∙cosα  .                                               (1)

 

 

 

С другой стороны, длину этой же стороны с по теореме косинусов находят через две другие стороны a,b треугольника и угол γ, против которого она лежит:                                  

                                 с = a∙cosβ +b∙cosα = .                       (2)

 В тоже время   сумму 2-х тригонометрических функций в (1), используя [2], можно представить в виде:

                                c= a∙cosβ +b∙cosα= a∙cosβ −b∙cosα' =     

                  =2

                 =                (3)                                                                                          

         Углы  в вершинах треугольника отсчитывают в одном направлении. Если  ось 0X  совпадает со стороной с треугольника и отсчет их производят против часовой стрелки [2], то в соотношении (3)  α'= π−α. Таким образом, имеем два представления для длины с стороны треугольника: (2) и (3). Найдем условие, при котором правые части формул (2) и (3) совпадают. Учитывая, что, а угол   под знаком радикала       

                                         ,                                (4)

получим соотношение         ,           (5)

которое тождественно правой части (2). Для полного совпадения (2) и (3) необходимо, чтобы второй сомножитель в формуле (3), а именно соsθ, был равен 1. Это достигается, если

                        .

Вычислим tgθ, как тангенс от суммы двух аргументов и, учитывая tgθ≡0, обратим в ноль числитель. После несложных преобразований получим, что

                            .            (6)

 В этом соотношении для суммы (разности) тангенсов от половинного аргумента сокращаем одинаковый знаменатель для слагаемых в квадратных скобках      (он отличен от нуля). В конечном итоге получаем математическое выражение

                                                      ,                                        (7)

которое есть теорема синусов для рассматриваемого косоугольного треугольника:          

Таким образом, формула косинусов (теорема о проекциях) есть частный случай (при учете теоремы синусов) обобщенной теоремы сложения для тригонометрических функций.

          II. Покажем, что теорему тангенсов и формулу тангенсов можно свести к одному и тому же  соотношению, каждая из них может быть преобразована в другую и наоборот. Приступая  к доказательству этого утверждения, уточним определения. Теорема тангенсов (в ряде источников ее называют формулой Региомонтана) связывает отношение разности 2-х сторон треугольника к их сумме с отношением тангенса половины разности противолежащих углов к тангенсу половины суммы этих же углов, рис.1):

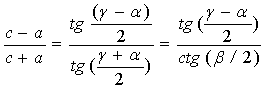                                                             .             (8)

 Формула тангенсов при  а > с   (рис.2):                                                             

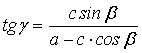                        .                                   (9)

Подпись: Рис. 2Подобные соотношения для других сторон и углов получают из формул (7),(8) при циклической перестановке сторон а,b,с  и соответственно противолежащих им углов α,β,γ.

 

Сначала преобразуем формулу тангенсов (9), чтобы получить угол γ в явном виде. Преобразуем числитель и знаменатель (9), выражая  аргументы тригонометрических функций  через половинный угол β/2.

                                  ;                   (10)

                          .        (11)

Подставим  (10) и (11) в соотношение (9) и получим, что

                 

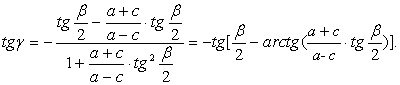
Откуда следует, что

                                  .             (12)

Теорему тангенсов (8) можно привести к такому же виду:

                                              

 Откуда                       

 Так как сумма всех углов треугольника  α +β +γ= π, то

                                      ;

и                             .

Окончательно, для угла γ:

                                    .                                      (13)

 Итак (12),(13) идентичны, формула Региомонтана и формула тангенсов тождественны и могут быть представлены совпадающими соотношениями (12), (13).

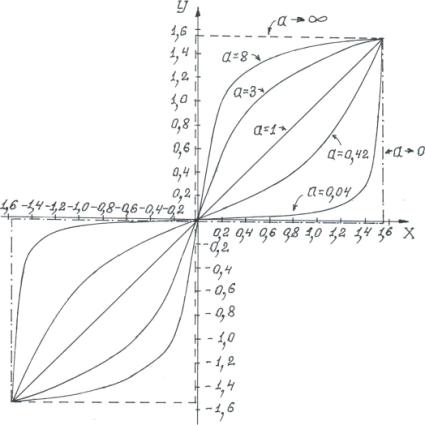
         III. Приложение: Функция  f(x)= arctg(a∙tgx) используется в [2]  и будет применяться в последующих публикациях. Поэтому исследуем ее поведение на интервале изменения аргумента − π/2 < х <π/2   и  параметра  0 <a<∞. На концах интервала, т.е. в точках х = ± π/2, функция не определена и имеет разрыв. Однако, поскольку существуют пределы

             lim f(x)=-π/2                              lim f(x)=+π/2  

             x→-π/2+0                                  x→π/2-0  ,                                                                                                                   

то, полагая  f(-π/2 ) и  f(π/2 ) равными именно этим значениям, получим, что  функция f(x) будет не только определена, но и непрерывна, включая крайние точки границы интервала. При а =1  f(x)=arctg(a∙tgx)≡х  по определению функции arctgx.  Соответственно при  х  >0

                        

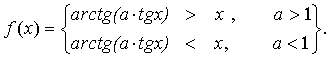
 В предельных случаяx а → 0 и а→+∞   график функции arctg(a∙tgx)  представляет отрезки прямых линий (рис.3).

Рассмотрим поведение функции f(x)=arctg(a∙tgx) при любых   -∞ <x < ∞. Для получения графика функции на интервале kπ-π/2<x<kπ+π/2, где к – любое целое число, полагаем z = x–kπ, тогда x = z +kπ, где  -π/2 ≤z ≤π/2:

               

Таким образом, область определения функции f(x)=arctg(a∙tgx) представляет собой бесконечное число открытых интервалов (kπ–π/2, kπ+π/2). В каждом

 

из этих интервалов функция f(x)  монотонно возрастает. Монотонность нарушается при a→0; a→∞. Точка пересечения ее графика с осью х − это одновременно и точка перегиба. Касательные в этих точках составляют с положительным направлением оси  х  угол ψ = arctga.

 

Рис.3. График функции y= arctg(a∙tgx)
 
 

 


 

Рис. 3. График функции Y= arctg(a∙tgx)

Выводы: Для плоского треугольника доказано, что формулу косинусов (теорему о проекциях) можно представить обобщенной формулой сложения [2]. Получено единое математическое соотношение для теоремы тангенсов и формулы тангенсов, что позволяет утверждать об их тождественности.

         Литература:

1.  Бронштейн И.Н., Семендяев К.А. Справочник по математике  для инженеров и  учащихся втузов. -13-е изд..- М.: Наука, гл. ред. физ.-мат. лит. 1986.- 544 с.

2. Комолов В.М.  Обобщение теорем сложения для тригонометрических функций. www.Rusnauka.com/, Материалы междунар. конф. «Современная Европейская наука-2014», London, Publishing House «Education and Science» s.r.o., Mathеmatics,Т.15,C.38-42.