И.А. Долгарев
ПОВЕРХНОСТИ
ПРОСТРАНСТВА-ВРЕМЕНИ ГАЛИЛЕЯ В ЯВНОМ ЗАДАНИИ
АННОТАЦИЯ. Явное
задание поверхности пространства-времени Галилея упрощает доказательство основной
теоремы теории поверхностей.
КЛЮЧЕВЫЕ СЛОВА. Задание поверхности одной функцией; метрическая функция поверхности;
форма кривизны галилеевой поверхности; определяемость галилеевой поверхности
метрической функцией и одним коэффициентом формы кривизны.
Регулярная
поверхность пространства-времени Галилея описывается векторной функцией
![]()
![]() ,
,
![]() , (1)
, (1)
здесь ![]() временной параметр,
временной параметр, ![]() пространственный параметр, [1]. Ввиду
регулярности поверхности, от параметризации (1) всегда можно перейти к
параметризации
пространственный параметр, [1]. Ввиду
регулярности поверхности, от параметризации (1) всегда можно перейти к
параметризации
![]()
![]() ,
, ![]() , (2)
, (2)
Пространственный
параметр обозначен через ![]() .
В [1] и последующих работах, в том числе и в [2], поверхности изучаются в параметризации (1). В геометрии евклидова
пространства, см., например, [3], рассматриваются явно заданные поверхности,
т.е. поверхности задаются одной функцией
.
В [1] и последующих работах, в том числе и в [2], поверхности изучаются в параметризации (1). В геометрии евклидова
пространства, см., например, [3], рассматриваются явно заданные поверхности,
т.е. поверхности задаются одной функцией ![]() ,
или в виде
,
или в виде ![]() ,
при этом некоторые формулы теории упрощаются. И поверхность
пространства-времени Галилея будем задавать одной явной функцией, как в (2).
Ниже установлено, что поверхность 3-мерного пространства-времени Галилея с
точностью до положении в пространстве определяется ее метрической функцией и
одним коэффициентом формы кривизны.
,
при этом некоторые формулы теории упрощаются. И поверхность
пространства-времени Галилея будем задавать одной явной функцией, как в (2).
Ниже установлено, что поверхность 3-мерного пространства-времени Галилея с
точностью до положении в пространстве определяется ее метрической функцией и
одним коэффициентом формы кривизны.
1.
Пространство-время
Галилея
В линейном пространстве ![]() действительного аффинного пространства
действительного аффинного пространства ![]() введено галилеево скалярное произведение
векторов. Пусть
введено галилеево скалярное произведение
векторов. Пусть ![]() =
=![]() базис пространства
базис пространства ![]() над полем
над полем ![]() действительных чисел. Галилеевым скалярным
произведением векторов
действительных чисел. Галилеевым скалярным
произведением векторов ![]() =
=![]() и
и ![]() =
=![]() называется число:
называется число:
![]() =
= 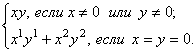 (3)
(3)
Линейное
пространство ![]() с галилеевым
скалярным произведением векторов называется галилеевым векторным пространством
с галилеевым
скалярным произведением векторов называется галилеевым векторным пространством ![]() , а аффинное пространство
, а аффинное пространство ![]() стало пространством-временем Галилея
стало пространством-временем Галилея ![]() . Галилеевой нормой вектора
. Галилеевой нормой вектора ![]() называется
называется ![]() =
=![]() и
и
![]() =
= 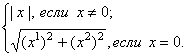 (4)
(4)
В ![]() неравенство
треугольника не выполняется. Векторы
неравенство
треугольника не выполняется. Векторы ![]() ,
, ![]() , называются
, называются
галилеевыми, или временными векторы ![]() называются евклидовыми.
Векторы из
называются евклидовыми.
Векторы из ![]() и точки пространства
и точки пространства ![]() называются еще событиями.
называются еще событиями.
Расстоянием ![]() между событиями
между событиями ![]() и
и ![]() называется:
называется:
![]() =
= 
Прямые и плоскости
аффинного пространства являются прямыми и плоскостями пространства Галилея ![]() . Репер
. Репер ![]() =
=![]() пространства
пространства ![]() считается
ортонормированным. Координатная плоскость
<O,
считается
ортонормированным. Координатная плоскость
<O, ![]() ,
,
![]() > является евклидовой, а плоскости <O,
> является евклидовой, а плоскости <O, ![]() ,
,![]() >, <O,
>, <O, ![]() ,
,![]() >
являются плоскостями Галилея – это 2-мерные галилеевы пространства. Через
всякую точку
>
являются плоскостями Галилея – это 2-мерные галилеевы пространства. Через
всякую точку ![]() галилеева
пространства
галилеева
пространства ![]() проходит единственная
плоскость Евклида, ее уравнение
проходит единственная
плоскость Евклида, ее уравнение ![]() ; таким образом, выполняется
; таким образом, выполняется
УТВЕРЖДЕНИЕ. В каждый момент времени в
пространстве-времени Галилея существует единственная плоскость Евклида.
Остальные плоскости
пространства Галилея, проходящие через точку
А есть плоскости Галилея. В пространстве ![]() временная
составляющая 1-мерна. Поэтому все галилеевы векторы пространства, временная
компонента которых имеет один и тот же знак, задают одно и то же временное
направление в
временная
составляющая 1-мерна. Поэтому все галилеевы векторы пространства, временная
компонента которых имеет один и тот же знак, задают одно и то же временное
направление в ![]() . Временное направление в
. Временное направление в ![]() в точке
в точке ![]() задается открытым
полупространством, границей которого является евклидова плоскость пространства
задается открытым
полупространством, границей которого является евклидова плоскость пространства ![]() , проходящая через точку
, проходящая через точку ![]() .
.
1. ЛЕММА. Всякий
галилеев вектор перпендикулярен всякому евклидову вектору.
# Галилеев вектор есть ![]() ,
,
![]() , евклидов вектор
, евклидов вектор ![]() .
Т.к.
.
Т.к. ![]() , то скалярное произведение
, то скалярное произведение ![]() вычисляется по первой строчке в определении
(3), получаем
вычисляется по первой строчке в определении
(3), получаем ![]() ,
что означает
,
что означает ![]() .
#
.
#
Для евклидова вектора
введена ![]() функция
(каппа-функция), получающаяся при дифференцировании единичного вектора, [1, c.
59].
функция
(каппа-функция), получающаяся при дифференцировании единичного вектора, [1, c.
59].
2.
ЛЕММА. В случае двумерного евклидова
вектора ![]() производная
единичного вектора направления
производная
единичного вектора направления ![]() равна
равна
![]() =
= ![]() ,
где
,
где ![]() ,
,
![]() . (5)
. (5)
Скалярный множитель ![]() в разложении (5) называется
в разложении (5) называется ![]() функцией
(каппа-функцией) евклидова вектора
функцией
(каппа-функцией) евклидова вектора ![]() ,
а также вектора
,
а также вектора ![]() .
.
Вектор ![]() =
= ![]() перпендикулярен вектору
перпендикулярен вектору ![]() единичной дли-
единичной дли-
ны, т.е. ![]() ,
,
![]() ,
,
![]() .
В галилеевой теории кривых кручением кривой
.
В галилеевой теории кривых кручением кривой ![]() называется
называется ![]() функция вектора
функция вектора ![]() ,
[1, c. 61].
,
[1, c. 61].
Линии и поверхности
аффинного пространства ![]() являются
соответственно линиями и поверхностями пространства-времени Галилея
являются
соответственно линиями и поверхностями пространства-времени Галилея ![]() . Галилеево скалярное произведение векторов выявляет
галилеевы свойства линий и
поверхностей.
. Галилеево скалярное произведение векторов выявляет
галилеевы свойства линий и
поверхностей.
1.
Регулярная поверхность
Изучается
регулярная поверхность
пространства-времени Галилея, заданная как отображение g : ![]() ®
® ![]() ,
и описываемая функцией
,
и описываемая функцией
![]()
![]() ,
, ![]() , (2)
, (2)
Функцию ![]() рассматриваем в виде
рассматриваем в виде ![]() . Составляющая
. Составляющая ![]() является временной, составляющая
является временной, составляющая ![]() является пространственной, т.е. евклидовой.
Векторы производных
является пространственной, т.е. евклидовой.
Векторы производных ![]() ,
, ![]() не коллинеарны. Всякая
точка
не коллинеарны. Всякая
точка ![]() поверхности
поверхности ![]() является обыкновенной. Поверхность
является обыкновенной. Поверхность
![]()
является проекцией
поверхности (2) на плоскость
Евклида. Имеется взаимно однозначное соответствие ![]()
![]() «
« ![]() Для частных производных
Для частных производных ![]() выполняются равенства:
выполняются равенства:
![]() ,
, ![]() ,
,
производные
![]() линейно независимы. Имеется касательная
плоскость поверхности (2)
линейно независимы. Имеется касательная
плоскость поверхности (2)
![]() =
= ![]() .
.
Она является галилеевой.
Вектор нормали ![]() касательной плоскости
касательной плоскости ![]() перпендикулярен и вектору
перпендикулярен и вектору ![]() .
Считаем вектор
.
Считаем вектор ![]() единичным, в соответствием с леммой 2, имеем
единичным, в соответствием с леммой 2, имеем
![]() . (7)
. (7)
Это вектор нормали
поверхности и, понятно, вектор нормали ![]() линии
поверхности. Нормаль поверхности
линии
поверхности. Нормаль поверхности ![]() во всякой ее обыкновенной точке
во всякой ее обыкновенной точке ![]() есть
есть ![]() =
= ![]() .
.
2. Основные квадратичные формы поверхности
Полный
дифференциал функции ![]() равен
равен ![]() .
Квадрат его длины
.
Квадрат его длины ![]() вычисляется в соответствии с (4):
вычисляется в соответствии с (4):
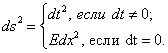 (8)
(8)
Значение
компоненты во второй строке:
![]() . (9)
. (9)
Функция ![]() называется метрической функцией поверхности
называется метрической функцией поверхности ![]() ,
она связана с измерениями на поверхности. Величина (8) называется метрической формой поверхности (2)
пространства Галилея.
,
она связана с измерениями на поверхности. Величина (8) называется метрической формой поверхности (2)
пространства Галилея.
На
поверхности (2) рассматривается произвольная галилеева линия, проходящая через точку Р:
![]() =
= ![]() . (10)
. (10)
Выписываем
вектор ![]() касательной к этой линии:
касательной к этой линии: ![]() =
= ![]() ,
, ![]() ,
, ![]() .
Продифференцируем его по
.
Продифференцируем его по ![]() :
:
![]() =
= ![]() + 2
+ 2![]()
![]() +
+
![]()
![]() .
.
Вектор ![]() нормали (7) поверхности (2) нормален
нормали (7) поверхности (2) нормален ![]() линии
поверхности в точке
линии
поверхности в точке![]() и, по лемме 1, нормален вектору
и, по лемме 1, нормален вектору ![]() .
Вектор нормали (7) записывается в виде
.
Вектор нормали (7) записывается в виде
![]() . (11)
. (11)
Линия
(10) является нормальным сечением поверхности ![]() (2). Поэтому, нормальная кривизна
(2). Поэтому, нормальная кривизна ![]() линий на поверхности:
линий на поверхности:
![]() .
.
В
равенстве ![]() =
= ![]() + 2
+ 2![]()
![]() +
+
![]()
![]() введем обозначения:
введем обозначения:
![]() = q,
= q,
![]() ,
,
![]() ,
,![]() . (12)
. (12)
Кривизна
линий на поверхности вычисляется по формуле
![]() = Aq2 +
2Bq + C,
(13)
= Aq2 +
2Bq + C,
(13)
коэффициенты
А,В,С вычислены в точке Р. Значение нормальной кривизны линий на
поверхности зависит от значения величины
q: ![]() – это функция
направления в области
– это функция
направления в области ![]() задания поверхности.
задания поверхности.
Вычислительные формулы
введенных коэффициентов (12) с учетом (11):
![]() ,
, ![]() ,
, ![]() . (14)
. (14)
Правую часть равенства (13) на
основе первого равенства из (12) записываем в виде квадратичной формы
![]() .
(15)
.
(15)
Она называется формой кривизны поверхности пространства-времени Галилея.
Коэффициенты формы кривизны поверхности (2) выписаны в (14).
3. Полная кривизна галилеевой поверхности. Некоторые свойства
поверхности
Нормальная
кривизна ![]() линии поверхности равна:
линии поверхности равна:
![]() = A.
(16)
= A.
(16)
Функция
![]() (13) обладает
экстремумом. Из
(13) обладает
экстремумом. Из ![]() : находим направление qэ экстремальной кривизны линий на поверхности:
: находим направление qэ экстремальной кривизны линий на поверхности:
![]() .
.
Экстремальное значение кривизны линий на
поверхности по (12) таково
![]() .
(17)
.
(17)
Имеется два главных направления на поверхности:
направление ![]() линии и экстремальное.
Произведение нормальных кривизн линий на поверхности в главных направлениях
называется полной кривизной поверхности:
линии и экстремальное.
Произведение нормальных кривизн линий на поверхности в главных направлениях
называется полной кривизной поверхности:
![]() . По (16) и (17):
. По (16) и (17):
![]() . (18)
. (18)
Для
поверхностей 3-мерного евклидова пространства установлено, [3], что
коэффициенты формы кривизны поверхности выражаются через коэффициенты
метрической формы. Тем самым изменяется содержание внутренней геометрии
евклидовых поверхностей. По виду коэффициентов метрической формы и формы
кривизны поверхности (9) и (14) приходим к выводу, что коэффициенты формы
кривизны галилеевой поверхности не выражаются через коэффициент метрической
формы. Галилеевы поверхности обладают традиционной внутренней геометрией.
Формула (18) полной кривизны поверхности позволяет классифицировать
обыкновенные точки поверхности, [2]. Для поверхности (2) по (18) и (14)
получаем:
![]() .
.
Эта формула полной крвизны галилеевой
поверхности совпадает с формулой полной кривизны евклидовой поверхности в явном
задании, см. [4, c. 263].
Если галилеева поверхность задана функцией (1),
то метрическая функция поверхности и коэффициенты формы кривизны вычисляются по
формулам:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (19)
. (19)
Формулы (9) и (14) проще только что приведенных.
4.
Основная теорема теории
поверхностей
В теории поверхностей пространства-времени
Галилея выполняется утверждение, аналогичное основной теореме теории
поверхностей 3-мерного евклидова пространства: регулярная евклидова поверхность
определяется с точностью положения в пространстве коэффициентами своих
метрической формы и формы кривизны (теорема Петерсона-Бонне), см. [3]. Заданы
дифференцирумые функции на односвязной области евклидовой плоскости ![]() ,
по коэффициентам (19) составлена система дифференциальных уравнений с частными
производными
,
по коэффициентам (19) составлена система дифференциальных уравнений с частными
производными
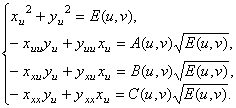 (20)
(20)
Решением
системы уравнений является семейство поверхностей (1), для которых заданные
функции служат метрической функцией и коэффициентами формы кривизны;
соответствующие начальные условия выделяют единственную поверхность с заданными
коэффициентами основных квадратичных форм.
Коэффициенты (9) и (14) позволяют получить систему
уравнений, проще чем (20).
Так
как по (9):![]() ,
то
,
то ![]() ,
,
![]() ,
следовательно, поверхность (2) определяется коэффициентами
,
следовательно, поверхность (2) определяется коэффициентами ![]() . Вместо системы уравнений (20) имеем
. Вместо системы уравнений (20) имеем
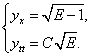 (21)
(21)
ТЕОРЕМА.
[5] Если на односвязной области
евклидовой плоскости заданы класса ![]() функции
функции ![]() ,
,
![]() ,
– метрическая функция и коэффициент формы
кривизны поверхности (2), то функция
,
– метрическая функция и коэффициент формы
кривизны поверхности (2), то функция ![]() ,
задающая галилееву поверхность (2) является
решением системы дифференциальных уравнений с частными производными (21). Начальные условия вида
,
задающая галилееву поверхность (2) является
решением системы дифференциальных уравнений с частными производными (21). Начальные условия вида ![]() ,
,
![]() ,
,
![]() выделяют
единственную поверхность, проходящую через точку
выделяют
единственную поверхность, проходящую через точку ![]() и
имеющую векторы касательных
и
имеющую векторы касательных ![]() ,
,
![]() .
Метрическая функция
.
Метрическая функция ![]() и
коэффициент
и
коэффициент ![]() формы кривизны найденной поверхности совпадают с заданными.
формы кривизны найденной поверхности совпадают с заданными.
Решение
системы уравнений (21) тривиально.
ПРИМЕР. Заданны функции: ![]() .
Отыскиваем функцию
.
Отыскиваем функцию ![]() .
По условию имеем:
.
По условию имеем:
![]() ,
, ![]() .
.
Последние
равенство дает ![]() .
Приходим к уравнению
.
Приходим к уравнению
![]() .
.
Его
решение есть 2-параметрическое семейство поверхностей ![]() .
Начальные условия
.
Начальные условия ![]() выделяют поверхности
выделяют поверхности
![]() ,
,
определяющие параболоиды – эллиптический и
гиперболический.
В линейное пространство аффинного
пространства могут быть введены различные скалярные произведения векторов, в
результате получаются евклидово, псевдоевклидово, галилеево и другие пространства.
Линии и поверхности аффинного пространства обладают как евклидовыми, так и
галилеевыми свойствами, выявляются они посредством введения соответствующего
скалярного произведения векторов. Можно определить галилеевы квадратичные формы
евклидовой поверхности и получить евклидову поверхность по заданным галилеевым
квадратичным формам, [6].
Список литературы
1. Долгарев А. И. Классические методы в дифференциальной
геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.
2. Долгарев И. А. Системы
дифференциальных уравнений в частных производных для поверхностей пространства
Галилея: дис. … канд. физ.-мат. Наук. -
Пенза: ПГУ, 2007. – 119с.
3. Долгарев А.И. Новый вид
основной теоремы Гаусса в евклидовой теории поверхностей. // Materiali IX mezinarodni vedecko-praktika conference «Dni
vedy – 2013» - Dil 32. Matematika. Vystavba a architektura: Praga. Publiching House “Education
and Skience”. s.r.o. – 2013. С. 55 – 60.
4. Рашевский П.К. Курс
дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.
5. Долгарев И. А. Галилеевы
квадратичные формы евклидовой поверхности.// Метрическая геометрия поверхностей
и многогранников – Междунар. конф. памяти Ефимова Н.В., МГУ, Москва, 18 – 21
авг. 1210. Сборник тезисов. – Москва: МАКС Пресс 2010. С. 24 – 25.
6. Долгарев И. А. и
Долгарев А. И. Галилеевы идеи в курсе
евклидовой дифференциальной геометрии.// Вестник Красноярского педуниверситета
им. В.П. Астафьева, 2013 № 1(23), Красноярск, 2013, С. 232 – 235.