Kraeva E.M.
Siberian State Aerospace University named after M.F.
Reshetnev, Russia
Calculation of turbulent flows for an centrifugal impeller
in a field of centrifugal forces
In the
centrifugal impellers of semi-open and open type, there is unevenness in flow and
vortex interaction along the radius main fluid flow and in the lateral axil of
the pump [1]. Blades convey energy to fluid flow, a portion of which moves in the
lateral axil with a lag from the main. In the result, flow is formed, the same
as in the channel behind the poorly streamlined body. This flow is
characterized by the appearance of return currents and vortices [2]. This
process is determined by the ratio of width to channel length, the thickness of
the boundary layer on the walls and the relative height of the blade.
Interaction of flows in the axil and in the channels leads to the circulation
of the vortex flow in the area behind the ledge.
For a centrifugal impeller, motion of fluid flow in the
circumferential direction in the gap 
with respect to
the blades leads to the formation the circulation zone in channels of the
impeller due to the stream flows around cavities. Interaction between the jet
and the liquid in the channels the impeller leads to the circulation flow in
the channel behind the blade.
The flow is uniform due to its
preload in the axial gap 
and parameters of circulation zone do not depend on the number 
due to self-similarity of turbulent jets [2].
Then for the mixing zone, position of its boundary with respect to the X-axis
can be written as
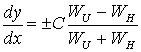, (1)
where Ñ
is experienced coefficient, 
[1].
(2)
For symmetric about the axis X boundaries of the mixing
zone 2, that separate the flow in the channel from the flow in the gap 
, its position can be defined by the
expression [3]
. (3)
To
investigate the pressure fields, we designed a special device that allowed to find
out the picture of the fluid flow in the channels of the impeller and to
measure pressure distribution along the channel walls.
Tests were
performed at an angular speed of rotation of the centrifugal impeller ω = 310
rad / sec.
Analysis of
obtained data gives reason to believe that the channels have the intense vortex
with an axis in the radial direction shifted to the pressure side of the blade.
In the relative motion value of the velocity with which the fluid flows around
channels, can be determined 
.
Circulation
zone in the channel can be divided into two areas: intensive rotational motion
in a circle with a radius râ, and the circulating
fluid motion along the trajectories of the elliptical character. Based on the
above, taking into account the equations (3) of the radius of the vortex zone
of intensive rotational motion is determined by the expression:
râ = 0.519 (b - 0,08829B). (4)
One of the
characteristics of the vortex area is the ratio of the circumferential velocity
and the free stream velocity Wu at the outer edge of the
vortex zone
.
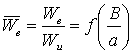Analytical
calculation of the value 
on the basis of the data in [2]
for channels of an impeller gives = 0.22. However, the experimental data [1]
give reason to take it equal to 0.3.
Then the
expression for the angular velocity of rotation of the vortex in channels of an
impeller at a radius R taking into account the values of 
= 0.3 and dependence (4) can be written as
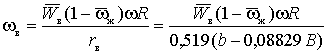. (5)
Experimental data generally confirm the accepted model of
jet-vortex flow in a three-zone field of centrifugal forces, which allows us to
calculate its parameters.
This work was
supported by the grant of the President of Russian Federation MK-1371.2013.8.
References
1. Kraeva E.M. High-speed centrifugal pump units. Siberian Stat
Aerospace University – Krasnoyarsk, 2011. - 212 p.
2. Abramovich G.N. The theory of turbulent
jets.
- Moscow. : Fizmatgiz,1960. -716 p.
3. Hagen R.L. Danak A.M. Heat transfer in the field of
the turbulent boundary layer separation over a dimple // Heat Transfer.1967. –
No 4. – P. 62–69.