The honored science and education member of the RANS, corresponding-member of the IAS of HS, Dr.S. (eng.). Professor,

Pil E.A. Russia, Saint-Petersburg,

VARIANTS OF MACROECONOMICS DEVELOPMENT AFTER BEING AFFECTED BY DIFFERENT FORCES

When affected by external or internal forces (or by both of them combined), economic shells deform, and their deformation can be sorted into the following types presented in the table.

At the simultaneous expansion (retraction) of economic shells (or at their expansion and retraction combined) it is implied that it may take place proportionally, i.e. according to one mathematical law and by one and the same relative value percentagewise, as well as disproportionally, i.e. according to different mathematical laws and by different values percentagewise.

Complex deformation of an economic shell is understood as deformation during which there is simultaneous influence of external and internal forces applied to different locations. That said in one or several areas the economic shell retracts under the influence of external forces, and in one or several locations it expands under the influence of internal forces. In this case external and internal forces affecting the economic shell may be similar or different in value.

As forces P_V affecting an economic shell may differ in their relative value, let us introduce the following three levels for them:

· P_b is a major external (internal) force;

· P_m is a medium external (internal) force;

· P_s is a minor external (internal) force.

In view of the fact that the table 1 has only 11 different variants from 64 according to which the change of all the three economic shells are possible, below we will view several of them, as the conclusions made for these variants will be valid for the rest of them.

Table 1 Types of economic shells deformation as affected by external and internal forces PV
№ п/п	Big business	Medium-size business	Small business
1.	with no changes	with no changes	with no changes
2.	with no changes	with no changes	expansion
3.	with no changes	with no changes	compression
4.	with no changes	with no changes	complex deformation
5.	with no changes	expansion	with no changes
6.	with no changes	expansion	expansion
7.	with no changes	expansion	compression
8.	with no changes	expansion	complex deformation
9.	with no changes	compression	with no changes
10.	with no changes	compression	expansion
11.	with no changes	compression	compression

The 1^st deformation type is that all the three economic shells stay unchanged

This state may be in the following three cases:

· where all the values of forces P_b, P_m, and P_s are equal to zero, i.e. P_b = P_m = P_s = 0;

· where all the values of forces P_b, P_m and P_s are very small and do not affect the economic shells that is why they can be ignored (Fig. 6а straight line 2);

where all the values of external and internal forces P_b, P_m, and P_s are balanced, as they act upon the same points of the economic shell from opposite sides.

Here P_b, P_m, and P_s – big, medium-size and small forces which influences on an economy shell.

This deformation type may be regarded as an exception. In this case all the three economic shells are active, i.e. all companies process their orders within the term, and the assets of enterprises stay unchanged. Here the population which also stays unchanged consumes all the produced goods and services. In other words there is balance set between consumption Qvc and produced goods Qvg and services Qvs. This balance can be noted down in the form of the formula Qvc = Qsg + Qvs. Quantity and quality of goods and services, as well as weather conditions do not change. There is no influence of adjacent space.

Let us introduce a new characteristic, the volume of an economic shell V_e which will allow us to note the following formulas of the case in question (1-3)

V_bb1 = V_bb2 = ,…, V_bbi = const. (1)

V_mb1 = V_mb2 = ,…, V_mbj = const. (2)

V_sb1 = V_sb2 = ,…, V_sbz.= const. (3)

Here V_bb is the volume of the economic shell of big business, unit³; V_mb is the volume of the economic shell of medium-size business, unit³, and V_sb is the volume of the economic shell of small business, unit³. The “unit” is understood to be a currency unit adopted in the country (countries) in question or its equivalent in the hard currency.

This state of economic shells may be represented in the more universal formula (4)

V_e = f(t) = const. (4)

where: V_e is the volume of an economic shell, unit³; f is a function (a mathematical dependence) according to which the state of an economic shell changes; t is time.

The 2^nd deformation type is that all the three economic shells expand

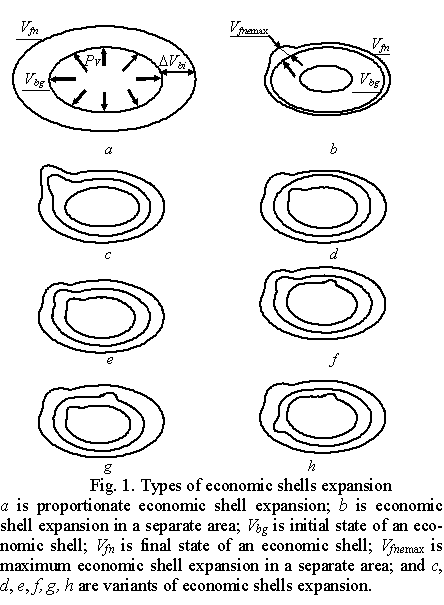
It can take place only in case all the forces act from within (Fig. 1).

In this case there may be the following three variants:

· all the economic shells expand in proportion to their previous states on all the axes (Fig. 1а);

· all the economic shells expand in disproportion to their previous states on all the axes;

· all the economic shells expand in one or several separate areas (Fig. 1b, 1c, 1d, and 1e).

Fig. 1b shows two economic shells for clarity, though in fact V_bg = V_fn. Here V_bg is the initial state of the volume of an economic shell before influence of external (internal) forces, unit³; V_fn is the final state of the volume of an economic shell after influence of external (internal) forces.

Let us view these expansions separately:

Proportionate expansion of all the economic shells means that they are affected by similar internal forces equally over the whole surface. In this case all the economic shells expand in proportion by certain percentage. Here we need to take into account that the forces affecting the economic shells in this case differ in value, as it is difficult to imagine that force acting upon the economic shell of small business may bring the same change to other economic shells percentagewise. Possible variants of shell expansion are presented in Fig. 2.

To describe the states of the shells let us introduce the value of relative increase (decrease) of the volume of an economic shell DV_er, as it allows us to characterize more fully the changed state of an economic cell and to compare them at their expansion and retraction (5)

DV_er = 100(V_fn – V_bg) / V_fn, % [or DV_er = (V_fn – V_bg) / V_fn]. (5)

where: DV_er is the value of a relative change of the volume of an economic shell, unit, (%). Value DV_er is better measured in percentage terms.

The value of a relative change may naturally be over one, as well as below one (a variant of the shell retraction), or equal to zero (a variant of insignificant affecting forces or slow response), i.e. we can note the following limits of existence of DV_er: 0 ³ DV_er ³ 1.

Now let us introduce the parameter that is the difference of the volumes of economic shell DV_e between the initial V_bg and final V_fn states which can be noted in the following form DV_e = V_fn – V_bg. (Fig. 2b)

Depending on the values of V_bg and V_fn the parameter DV_e may be positive at V_fn > V_bg where the economic shell expands (Fig. 2), as well as negative at V_bg > V_fn where the economic shell retracts (Fig. 4), or equal to zero DV_e = 0 (this case is described above in the first deformation type section). Economic shell expansion corresponds to the market activation, and its retraction means a situation of crisis.

Let us designate the time in which an economic shell expands (retracts) as Dt_e (Fig. 2d), and it is calculated according to the formula (6)

Dt_e = t_fn - t_bg = (t_in - t_bg) + (t_fn - t_in). (6)

In order for all the three economic shells to expand (retract) in proportion by the same percentage, let us introduce the value of the expansion (retraction) coefficient K_ec which indicates by how much we need to increase (or decrease) the force affecting small, medium-size or big business so that the other shells undergo similar proportionate changes, i.e. we can note down, for example, P_mb = K_eci P_sb or P_bb = K_ecj P_sb. Here indications “i” and “j” of coefficients K_ec are introduced in order to differentiate them for medium-size and big business respectively.

As in the case in question a certain number of forces act on an economic shell, they can be presented as follows (7)

If we apply the coefficient K_ex deduced above, we can note down the universal formula (8)

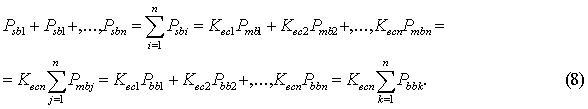
In view of the fact that in the example in question we see proportionate expansion of all the economic shells, the quantity of forces affecting them theoretically must be the same which is presented in the formula (8). In practice the quantity of forces affecting the economic shells may naturally vary.

For the values of the expansion (retraction) coefficient of an economic shell we can note down the following limits 0 > K_ec >> 1.

Based on these formulas we can suggest the following definition for the case in question:

Knowing the values of forces acting upon one of the economic shells and the values of expansion (retraction) coefficients K_ec, for the given forces we can calculate the value of expansion (retraction) of other economic shells.

The formula (8) is universal and it can be regarded as a “fundamental” law in economics, as it is true not only for this case in question, but for all other variants presented in the table. If we integrate the formula (8) over time we will be able to learn when and how the economic shells will change and to have time to react to these changes so that to minimize negative factors. Thus, we will be able to forecast future changes in economic shells by influencing them at this moment due to external and internal forces affecting them.

As economic shells cannot expand significantly over a short time period, let us introduce the notion of a coefficient of maximum single expansion K_ecemax and time t_ecemax within which this expansion can take place. The values of K_ecemax will be within the following limits: 0 > K_ecemax > 1. Here we must mention at once that t_ecemax 0. Thus, we can note down the value of a single final state of the volume of an economic shell after internal forces affect it (9)

V_fn = K_ecemax V_bg f(t_ecemax). (9)

Now let us introduce value DV_en by which the volume of an economic shell may increase (decrease) in case of a maximum single expansion (retraction). It is calculated according to the formula (10)

DV_en = V_fn - V_bg. (10)

Economic shells expand in one or several separate areas. Fig. 1b, 1c, 1d, 1e, and 1f present possible variants of such expansion which may be the following:

· One economic shell expands in a location and two others fully expand proportionally or disproportionally (Fig. 1b). Based on this let us introduce the value of the maximum flexure of an economic shell V_fnemax which shows how its volume can change so that it does not change into a higher economic shell. This value is applicable for medium-size and small business, but it is invalid for the case presented in Fig. 1с;

· Two economic shells expand in one location, and the third one expands proportionally. Economic shells expansion in one location is understood to be an expansion where the vector of forces acting on these shells is situated on one line that is perpendicular to the points in question. In this case deformation may take place on two neighboring shells, i.e. on the economic shells of medium-sized and big business (Fig. 1с) or on the shells of medium-sized and small business. Deformations of economic shells may also take place through a shell, i.e. economic shells of small and big business expand in certain areas (Fig. 1d), while the economic shell of medium-sized business expands proportionally. Here we may see a variant in which during deformation of two neighboring economic shells expansion of the smaller one will pass through the bottom limit of the higher shell (Fig. 1с). Then the question arises if we can already attribute this company to the new economic shell, in our example to big business. In order for us not to face any conflict in examples like this further, let us consider a company (companies) to have in fact changed one economic shell to another only if it has definitely merged with or crossed another economic shell in some point or area, i.e. in our example a company of medium-sized business will stay in it. This example is not covered by the law where, for instance, the economic shell of medium-sized business passes through the former bottom limit of big business while expanding, as the limits of big business have moved towards increase together with it. This law is also false for proportional retraction, but not for small business, especially if there is only one person working for a company;

· All three economic shells expand in one location (Fig. 1e);

· Two economic shells expand in one location and the third one in another location (Fig. 1f and 1g);

· Three economic shells expand in different locations (Fig. 1h).

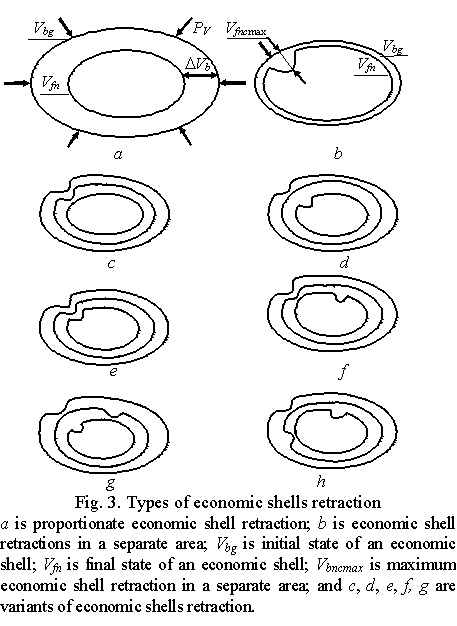
The 3^rd deformation type is that all the three economic shells retract

In this case all the forces acting upon economic shells act from the outside (Fig. 3).

In such event the following three variants are possible:

· all the economic shells retract in proportion to their previous states on all the axes (Fig. 3а);

· all the economic shells retract in disproportion to their previous states on all the axes;

· all the economic shells retract in one or several separate areas (Fig. 3b).

· Fig. 3b shows two economic shells for clarity though in fact V_bg = V_fn.

Let us view these retractions separately:

Proportionate retraction of all the economic shells means that they are affected by similar external forces equally over the whole surface. In this case all the economic shells retract in proportion by certain percentage. Here we also need to take into account that the forces affecting the economic shells in this case differ in value.

Similarly with the material described above let us introduce the notion of a coefficient of maximum single retraction K_eccmax and time t_eccmax within which this retraction can take place.

Thus, we can note down the value of a final state of the economic shell volume after external forces affect it (11)

V_fn = K_eccmax V_bg f(t_eccmax). (11)

If an economic shell moves into the area of another economic shell while retraction, it becomes part of this shell and all the laws of this economic shell are true for it. But this is not true for the variant shown in Fig. 3с. When small business “slips through” its bottom limit it stops acting, i.e. goes bankrupt.

Disproportionate retraction of all the economic shells. In case similar external forces affect all the three economic shells at once, their reaction will be different, thus, retraction of volume of these shells will change in different ways. In this case the following equations according to the rules must be true where the big business economic shell retracts by the value -DB_b (-DB_bmax) (12)

A similar formula can also be noted down in case medium-sized business is affected by external forces where the economic shell of medium-sized business retracts by the value -DM_b (-DM_bmax) (13)

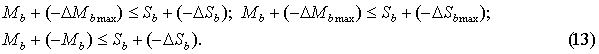
Economic shells retract in one or several separate areas. Fig. 3b, 3c, 3d, 3e, 3f, and 3h present possible variants of such retraction which can be the following:

· One economic shell retracts in a location and two others fully retract proportionally or disproportionally (Fig. 3b);

· Two economic shells retract in one location, and the third one retracts proportionally. Economic shells retraction in one location is understood to be a retraction where the vector of forces acting on these shells is situated on one line that is perpendicular to the points in question. In this case deformation may take place on two neighboring shells, i.e. on the economic shells of medium-sized and big business (Fig. 3с), or on the shells of the small and medium-sized business. Deformations of economic shells may also take place through a shell, i.e. economic shells of small and big business retract in certain areas (Fig. 3d), while the economic shell of medium-sized business fully retracts;

· All three economic shells retract in one location (Fig. 3e);

· Two economic shells retract in one location, and the third one in another location (Fig. 3f and 3g);

· Three economic shells retract in different locations (Fig. 3h).

The 4^th deformation type is that the shells of big and medium-sized business expand and the shell of small business retracts

This case is presented in Fig. 4.

That said there might be the following three variants:

· two economic shells expand and one retracts in proportion to their previous states on all the axes (Fig. 4а);

· two economic shells expand and one retracts in disproportion to their previous states on all the axes;

· two economic shells expand and one retracts in one or several separate areas (Fig. 4b).

· This deformation type of economic shells where medium-sized and big businesses expand is possible within the following variants:

· The shells of medium-sized and big business expand due to acquisition of small business;

· The shells of medium-sized and big business expand due to laws in force having negative effects on small business;

· The shells of medium-sized and big business expand due to acquisition of small business and laws in force having negative effects on small business.

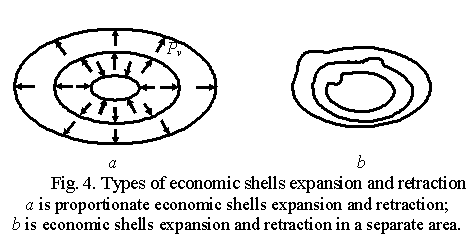
For this deformation type the descriptions made above for economic shells expansion and retraction are applicable.

However, we must specify here that acquisition of small business will lead to unbalanced percentage of the number of small business to medium-sized and big business companies and, moreover, this leads to monopolization of certain areas of the economy with all that it implies.

The 5^th deformation type is that the big business shell expands and the shells of medium-sized and small business retract

This type of economic shells deformation is presented in Fig. 5 and similar conclusions made above are true for it.

Here three similar variants are possible:

· one economic shell expands and two retract in proportion to their previous states on all the axes (Fig. 5а);

· one economic shell expands and two retract in disproportion to their previous states on all the axes;

· one economic shell expands and two retract in one or several separate areas (Fig. 5b).

This case means that big business acquires medium-sized and small ones which will lead primarily to price growth for goods and services that disappear when small and medium-sized companies go bankrupt or are acquired by big business.

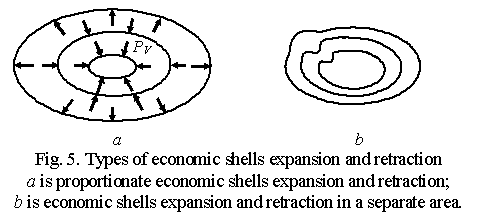
The 6^th deformation type is that the shells of big and small business retract and the medium-sized business shell expands

For this deformation type there are the following three variants possible:

· two economic shells expand and one retracts in proportion to their previous states on all the axes (Fig. 6а);

· two economic shells expand and one retracts in disproportion to their previous states on all the axes;

· two economic shells expand and one retracts in one or several separate areas (Fig. 11b).

In the type of deformations in question there is an interesting case represented in Fig. 11b where the big business shell retracts in one location, and the medium-sized business shell expands in the same location winning new released market outlets. When these two economic shells intercross, a company (companies) of medium-sized business change places with a company (companies) of big business. Let us call this process “rotation” of a company and give it the following definition.

The process of a company (companies) moving from a lower economic shell to a higher one due to increased production of a goods or services in a certain market area released by a company (companies) from a higher shell is called rotation.

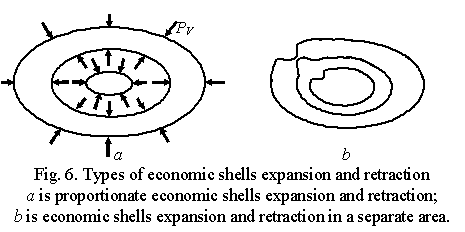
Thus, one company (companies) was gradually replaced by another company (companies).

The 7^th deformation type is that the shells of big and medium-sized business expand and the small business shell stays unchanged

For this deformation type there are the following three variants possible:

· two economic shells expand in proportion to their previous states on all the axes (Fig. 7а);

· two economic shells expand in disproportion to their previous states on all the axes;

· two economic shells expand in one or several separate areas (Fig. 7b).

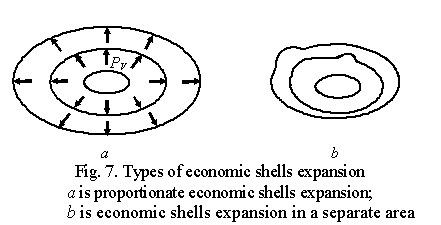
If two economic shells expand, and small business stays unchanged, thus, either it was influenced by the country’s legislation and the population doesn’t want to develop it, or big and medium-sized businesses have taken over the markets and do not let small business develop.

The 8^th deformation type is that the shells of big and medium-sized business retract and the small business shell stays unchanged

For this deformation type there are the following three variants possible:

· two economic shells retract in proportion to their previous states on all the axes (Fig. 8а);

· two economic shells retract in disproportion to their previous states on all the axes;

· two economic shells retract in one or several separate areas (Fig. 8b).

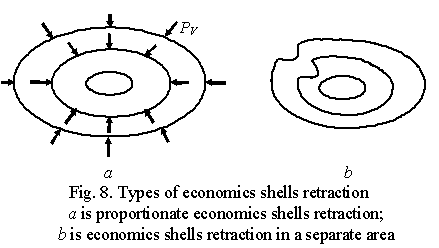
This variant shows worsening economic state of markets for big and small business due to decreasing purchasing power of the population which can afford mostly inexpensive goods, services and food. This will concern employees of big and medium-sized business, as either their salaries will decrease, or they will be excessed. As for the number of small business employees and their salaries, they will not change, that is why their consumer basket will stay unchanged.

As the main economic index of any country is gross domestic product (GDP), let us introduce the notion of theoretical GDP volume of a state V_TGDP that will be constructed from the total of theoretical volumes of economic shells of big V_tbbi, medium-sized V_tmbj and small business V_tsbz.