Экономические науки/8. Математические методы в экономике

К.ф.-м.н. Попова Н.В.

Федеральное государственное бюджетное образовательное учреждение высшего образования «Российский экономический университет имени Г.В. Плеханова»

Теоремы об оценке облигаций как математические

Известны пять теорем об оценке облигаций [1; 2, С. 456-458]. Это теоремы о свойствах цены облигации. Теоремы сформировались в результате наблюдений на рынке облигаций. В работе [1] они сформулированы и доказаны как математические теоремы. Применение математических методов в анализе инвестиций за последние десятилетия признано эффективным и необходимым. Появились другие доказательства этих теорем, например в работах [3,4,5], их обобщение на облигации, по которым основная сумма долга выплачивается в течение долгого времени, например, ипотечные облигации [6].

Представление теорем как математических потребовало сформулировать условия, при которых утверждения теорем верны, и предложить подходящий математический аппарат. Теоремы доказаны в условиях определенности: облигация не имеет кредитного риска и не может быть отозвана эмитентом до установленной даты погашения. Для доказательств использованы следующие теоремы из математического анализа: критерий монотонности дифференцируемой функции, теорема Лагранжа, критерий выпуклости дважды дифференцируемой функции. В теоремах доказаны зависимости от доходности и срока до погашения абсолютного или относительного (процентного) изменения цены облигации. Возникает вопрос: для чего нужны математические доказательства? Что они дают нового?

Известно, что примеры и эксперименты для математики не имеют доказательной силы. Лишь после того, как получено математическое доказательство, утверждение приобретает «абсолютный и вечный» характер, как всякая математическая истина (при тех условиях, при которых доказано утверждение). Таким образом, наличие математического доказательства некоторого утверждения о свойствах объекта инвестирования изменяет статус этого утверждения. Это уже не просто утверждение на основе отдельных, хотя и часто встречающихся наблюдений. Утверждение, будучи доказанным, выражает объективно существующее явление, проявляющееся при определённых условиях, и может быть использовано как данность в других исследованиях. Согласно [2, С.458], свойства цены, сформулированные в этих теоремах, «важны для прогнозирования влияния процентных ставок на курсы облигаций».

Можно отметить и другие преимущества применения математических методов в финансовом анализе. Можно утверждать, что математические доказательства свойств облигации в некоторых случаях позволяют объяснить, с чем эти свойства связаны. Например, теорема о зависимости величины изменения цены облигации от направления изменения её доходности (теорема 4 Малкиела [1], другое доказательство в работе [4, С. 129-130]). Из доказательства теоремы следует, что наблюдаемое на рынке свойство цены облигации, такое как большая чувствительность цены к снижению доходности к погашению, нежели чем к ее увеличению объясняется выпуклостью зависимости цена – доходность.

Применение математических методов показало также их возможности уточнять свойства цены облигации. Например, теорема о зависимости цены облигации от срока до погашения (теорема 3 Малкиела [1], другое доказательство в работе [3, С. 23]). Доказано не только само утверждение о поведении цены облигации при фиксированной доходности, но и установлен характер зависимости цена – срок до погашения. При условии неизменности доходности к погашению цена облигации, продающейся с премией (дисконтом), является возрастающей вогнутой (убывающей выпуклой) функцией числа купонных периодов до погашения.

В настоящее время теоремы, впервые доказанные Малкиелом в [1], являются основой теории финансовых инвестиций с фиксированным доходом в условиях определенности. Несмотря на серьезные ограничения этой теории, ее результаты необходимы как часть общей теории инвестирования. В рамках этой теории доказаны основные инвестиционные свойства облигации [3,4]. Очевидно, что развитие и углубление этой теории имеют значение не только для самой теории, но и для практического инвестирования, так как способствуют обоснованности инвестиционных решений. Ниже приводится доказательство одной из теорем в этой теории. Теорема посвящена влиянию уровня процентных ставок рынка на величину изменения цены облигации при изменении её доходности на заданную величину. Согласно [7, С. 507], «Чем выше уровень доходности, тем ниже изменчивость цены». Изменчивостью цены называют относительное изменение цены облигации при изменении рыночной процентной ставки. Математическая теорема для доказательства данного утверждения имеет следующий вид:

Теорема. Чем выше уровень процентных ставок рынка, тем меньше абсолютное и относительное изменение цены облигации при изменении ее доходности на заданную величину.

Доказательство. Пусть r – исходный уровень доходности. Предположим для определённости, что доходность облигации увеличилась на величину (это заданная величина, не зависит от r). Требуется доказать, что абсолютное и относительное снижения цены облигации при увеличении ее доходности на величину − убывающие функции r.

Дифференцируем: , поскольку − выпуклая функция и её производная – возрастающая функция на множестве . Как видим, поведение абсолютного изменения цены облигации объясняется выпуклостью зависимости цена - доходность.

Докажем утверждение теоремы об относительном изменении цены облигации. Дифференцируем:

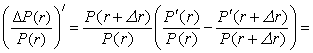
поскольку и , где и – дюрация облигации при уровнях доходности и r соответственно. Теорема доказана. Другое доказательство этой теоремы можно посмотреть в работе [8].

В табл. 1 показано поведение величин и купонной облигации в зависимости от r для Δr = 0,1%. Как видим, вычисления подтверждают утверждения теоремы и соответствуют рыночным наблюдениям.

Таблица 1

A = 100, m = 1, f = 10%, n = 5, Δr = 0,1%.

r
1%	143,681	139,269	4,412	0,0307
2%	137,708	135,463	2,245	0,0163
3%	132,058	130,581	1,477	0,0112
4%	126,711	125,625	1,086	0,0086
5%	121,647	120,798	0,849	0,0070
6%	116,849	116,159	0,691	0,0059
7%	112,301	111,723	0,577	0,0051
8%	107,985	107,492	0,493	0,0046
9%	103,890	103,462	0,427	0,0041
10%	100,000	99,625	0,375	0,0038
11%	96,304	95,971	0,333	0,0035
12%	92,790	92,493	0,298	0,0032
15%	83,239	83,017	0,222	0,0027
18%	74,983	74,810	0,173	0,0023
20%	70,094	69,945	0,149	0,0021

Из доказательства второй части теоремы следует, что данное свойство изменчивости цены облигации объясняется зависимостью дюрации облигации от её доходности. Если учесть, что по величине оценивают процентный риск облигации, а дюрация облигации рассматривается как мера её процентного риска, то это объяснение согласуется с выводом о поведении процентного риска облигации, который можно сделать на основе свойств дюрации. А именно: чем выше доходность облигации, тем меньше её дюрация, а, следовательно, тем меньше её процентный риск, т.е. величина . Теорема доказана в условиях определенности. Доказательства других теорем в условиях определенности можно посмотреть в работах [9-11].

Вывод. Представление в работе [1] теорем, связанных с оценкой облигаций, как математических показало преимущества математических методов и положило начало развитию теории финансовых инвестиций с фиксированным доходом в условиях определенности. Результаты этой теории необходимы при принятии инвестиционных решений.

ЛИТЕРАТУРА

1. Malkiel B. Expectations, bond prices, and the term structure of interest rates. – Quarterly Journal of Economics, 1962, Vol.76, No.2. – p.197–218.

2. Шарп У. Ф., Александер Г. Дж., Бэйли Дж. В. Инвестиции. – М.: ИНФРА-М, 1999. – 1028 с.

3. Барбаумов В. Е., Гладких И. М., Чуйко А. С. Финансовые инвестиции с фиксированным доходом (количественный анализ): Учебное пособие. – М.: Изд-во РЭА им. Г.В.Плеханова, 2006. - 112 с.

4. Мельников А.В., Попова Н.В., Скорнякова В.С. Математические методы финансового анализа. М.: АНКИЛ, 2006. – 440 с.

5. E.R. Lawrence and S.Shankar A Simple and Student-Friendly Approach to the Mathematics of Bond Prices. Quarterly Journal of Business and Economics, Vol. 46, No. 4 (Autumn, 2007), pp. 91-99.

6. Joel R. Barber A General Relationship between Prices of Bonds and their Yields. Quarterly Journal of Finance and Accounting. Vol. 49, No. 3/4 (Summer/Autumn 2010), pp. 75-85.

7. Фабоцци Ф. Дж. Управление инвестициями. – М.: ИНФРА-М, 2000.– 932 с.

8. Попова Н. В. Рыночные теоремы и их продолжение // Вестник РЭУ им. Г.В. Плеханова. – 2013. – № 7(61). - С. 93 - 101.

9. Попова Н.В. Влияние срока до погашения на изменчивость цены облигации. Вестник финансового университета. № 3(75), 2013. С.72-84

10. Барбаумов В.Е., Попова Н.В. Влияние уровня доходности рынка на поведение цены облигации. Менеджмент и Бизнес-Администрирование. №3, 2015. С. 52-57.

11. Попова Н.В. Влияние частоты купонных платежей на показатель дюрации облигации. Вестник финансового университета. № 4(88), 2015. С.104-115.