Д.т.н., професор Лукашенко В.М., к.т.н., доцент Уткіна Т.Ю.,
к.т.н. Лукашенко А.Г., аспірант Лукашенко Д.А., Дубіцький К.О.

Черкаський державний технологічний університет, Україна

МЕТОДИКА ФУНКЦІОНАЛЬНОГО АНАЛІЗУ МНОЖИНИ
МОДЕЛЕЙ АКСЕЛЕРОМЕТІВ

Область застосування інтегральних акселерометрів є надзвичайно широкою: від аерокосмічної техніки до робототехніки. Це обумовлює широкий діапазон пропонованих до них вимог за основними параметрами. Питанням побудови, управління й застосування акселерометрів присвячено ряд робіт А. Юдіна, О. Коленченко, С. Сисоєвої, Д. Ларіонова, О. Казакевича, А. Лєбєдєва, І. Петрова, О. Тузова, B. Scannell, V. Lara, Ch. J. Fisher та інших. Однак, в цих роботах недостатньо відображено, як із безлічі сучасних моделей акселерометрів швидко вибрати найкращу або визначити вузьке місце для подальшого її вдосконалення. Задача особливо актуальна при відсутності математичного опису багатьох взаємозв’язаних параметрів моделей акселерометрів [1-2].

Метою роботи є прискорення процедури визначення найкращої моделі або вузького місця у множині сучасних моделей акселерометрів для рекомендації їх усунення за рахунок синтезу теорії неповної подібності та розмірностей з використанням діаграм Венна.

Для досягнення цієї мети поставлені та вирішені наступні задачі:

- складено перелік сучасних моделей акселерометрів з основними технічними параметрами;

- створено узагальнену математичну модель за основними технічними параметрами акселерометрів;

- виявлена наявність взаємозв’язку між параметрами та при відсутності її аналітичного виразу використовуються властивості теорії неповної подібності та розмірностей;

- на підставі евристики створені умовні критерії подібності та їх фізичне тлумачення;

- побудовано багатокритеріальну знакову модель залежності основних технічних параметрів сучасних моделей акселерометрів у безрозмірних координатах з використанням діаграм Венна;

- проведено функціональний аналіз множини акселерометрів та запропоновані рекомендації щодо усунення вузького місця у відповідних підмножинах акселерометрів.

Рішення поставленої задачі. Відомо [3-4], що фізичне моделювання на основі теорії неповної подібності та розмірностей з використанням діаграм Венна є одним з ефективних методів вирішення таких складних задач при проектуванні нових компонентів. Це дозволяє спростити процес визначення близького по суті прототипу та визначити напрямки вдосконалення існуючих сучасних компонентів, що скорочує час на проектування і, як наслідок, знижує вартість компонентів. Запропонована методика функціонального аналізу множини компонентів, алгоритм якої містить задачі, що зазначені вище, показана на прикладі 8 типів акселерометрів. Їх перелік наведено в табл. 1.

Таблиця 1

Перелік сучасних моделей акселерометрів з основними технічними параметрами та умовні критерії подібності

№	Фірма	Модель	Діапазон вимірюваних прискорень (g)	Діапазон робочих температур, K		Умовні критерії подібності
				min	max	KQ	KG
1	Analog Devices	ADXL313	±0,5/ ±1,.0 / ±2 / ±4,0	233	378	0,38	4
2		ADXL345	±2 / ±4 / ±8	243	358	0,32	3
3	Bosch Sensortec	BMA280	±2 / ±4 / ±8	233	358	0,35	3
4		BMA250E	±2 / ±4	243	348	0,30	2
5	Murata	SCA830-D06	±1 / ±2	243	398	0,39	2
6		SCA3100-D07	±5 / ±6	243	393	0,38	2
7	STMicroelectronics	AIS326DQ	±2 / ±6	243	378	0,36	2
8		LIS2DS12	±2 / ±4 / ±8 / ±16	243	358	0,32	4

Узагальнена математична модель за основними технічними параметрами акселерометрів, що приведені в табл. 1, має наступний вигляд:

(1)

де  – максимальні і мінімальні значення температури акселерометра; – кількість діапазонів вимірюваних прискорень акселерометра.

З формули (1) видно відсутність аналітичного виразу між параметрами.
В цьому випадку застосовуються властивості теорії неповної подібності та розмірностей і створюється критеріальне рівняння на основі прийнятих критеріїв, що приймає наступний вигляд

(2)

де 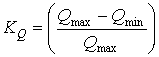 – величина, яка характеризує температурний діапазон акселерометра.

Результати розрахунку умовних критеріїв наведені в табл. 1.

На базі критеріального рівняння (2), π-теореми та даних акселерометрів (табл. 1) будується функція критеріїв за основними технічними параметрами в безрозмірних координатах.

Для функціонального аналізу універсальної множини  та наглядного відображення співвідношень між підмножинами будуються діаграми Венна.

На рис. 1 сформована універсальна множина , яка представляє сукупність 8 сучасних моделей акселерометрів, та поділена на підмножини

Сукупність умовних критеріїв обраних моделей акселерометрів, що утворюють множину , має наступний опис

(3)

Функціональний аналіз універсальної множини  та наглядне зображення співвідношень між підмножинами прискорюється завдяки візуалізації розташованих підмножин сучасних моделей акселерометрів. Це дозволяє визначити найкращі та рекомендувати напрямок їх удосконалення наступним чином. Компоненти підмножини  мають найбільшу кількість діапазонів вимірюваних прискорень, в порівнянні з моделями підмножини , а моделі підмножини  мають найбільший температурний діапазон в порівнянні з моделями підмножини .

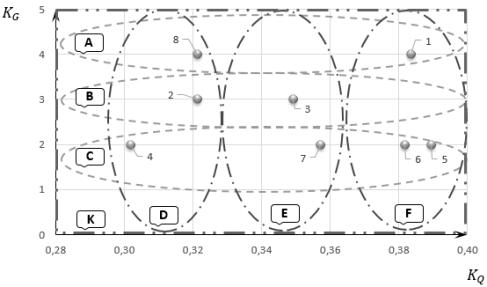
Рис. 1. Багатокритеріальна знакова модель залежності основних технічних параметрів
в безрозмірних координатах для сучасних моделей акселерометрів

Примітка: цифри 1, 2, …, 8 відповідають цифрам в табл. 1.

Підмножина, що утворена перетином (A Ç D) – має найбільшу кількість діапазонів вимірюваних прискорень та низький температурний діапазон, тому її доцільно вдосконалювати за напрямком збільшення температурного діапазону. Підмножина, що утворена перетином (A Ç F) – має широкий робочий температурний діапазон та найбільшу кількість діапазонів вимірюваних прискорень, тому за розглянутими параметрами – це найкращі моделі. Підмножина, що утворена перетином (C Ç D) – має вузький температурний діапазон та малу кількість діапазонів вимірюваних прискорень, тобто має найгірші параметри. Це відноситься до моделі № 4 AIS326DQ фірми STMicroelectronics. Підмножина, що утворена перетином (C Ç F) – має широкий температурний діапазон та малу кількість діапазонів вимірюваних прискорень: рекомендується напрямок удосконалення по розширенню діапазонів вимірюваних прискорень.

Запропонована методика функціонального аналізу підмножин універсальної множини  дозволила одночасно за робочим температурним діапазоном та кількістю діапазонів вимірюваних прискорень сучасних моделей акселерометрів виділити найкращу модель № 1 ADXL313 фірми Analog Devices.

Висновки:

1. На основі створеного переліку моделей акселерометрів створена узагальнена математична модель, аналіз якої показав відсутність аналітичного опису між визначеними технічними параметрами.

2. Визначено фізичне моделювання та розроблені умовні критерії подібності, на підставі яких побудована багатокритеріальна знакова модель функції критеріїв подібності в безрозмірних координатах для 8 моделей акселерометрів, яка завдяки використанню діаграм Венна поділена на підмножини.

3. В результаті проведеного функціонального аналізу універсальної множини визначено, що найкращим акселерометром є № 1 ADXL313 фірми Analog Devices та надані рекомендації для інших акселерометрів за напрямками вдосконалення.

Перспективою подальших досліджень є імплементація методики функціонального аналізу при проектуванні сучасних складних моделей комп’ютерних систем.

Література:

1. Юдин А. Новые акселерометры компании STMicroelectronics / А. Юдин // Компоненты и технологии. – 2009. – № 2. – С. 28–31.

2. Лебедев А. Цифровые МЭМС акселерометры в automotive-исполнении / А. Лебедев // Современная электроника. – 2008. – № 5. – С. 12–15.

3. Лукашенко А. Г. Виявлення резерву предмета дослідження на основі теорії неповної подібності та розмірностей / А. Г. Лукашенко, О. А. Кулигін, В. М. Лукашенко // Вісник ХНУ. – 2009. – № 3. – С. 184–187.

4. Рудаков К. С. Двоквадрантна образно-знакова модель визначення ефективного маршрутизатора / К. С. Рудаков, В. М. Лукашенко, Т. Ю. Уткіна // Вісник ХНУ. – 2015. – № 2. – С. 150–156.