Математика. Дифференциальные и интегральные уравнения 

 

к.ф.-м.н. Терентьев А.М. 

Нижегородский государственный университет им. Н.И. Лобачевского, Россия

 

Исследование динамической системы, моделирующей классический электродный эффект

 

Основы теории электродного эффекта заложены в новаторских работах Дж. Томсона (лорд Кельвин) и У. Свана [1, 2]. Классический электродный эффект для приземной атмосферы изучался многими авторами [3–5]. Однако, в большинстве работ рассмотрены приближенные или численные методы ввиду отсутствия полного аналитического и качественного исследования математической модели соответствующей классической задачи электродного эффекта.

В статье рассматривается система дифференциальных уравнений

                                                                                 (1)

                                                                               (2)

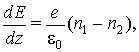                                                                                       (3)

описывающая динамику электродного эффекта в приземных слоях атмосферы при отсутствии ядерной конденсации [3, 4]. Здесь , ,  – неизвестные функции ; , , q, , e,  – положительные константы. Проводится полное исследование рассматриваемой системы на фазовой плоскости .

 

Преобразование исходной системы

Уравнения (1), (2) с учетом (3) записываются следующим образом:

                   

 

                      

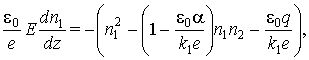
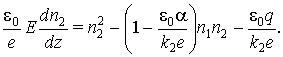
Тогда, используя обозначения 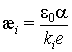 (), исходная система (1)–(3) представляется в эквивалентном виде

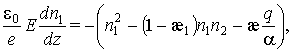                                                         (4)

                                                           (5)

                                                                                       (6)

Ставится задача проведения полного качественного исследования уравнения фазовых траекторий, соответствующего (4), (5).

Особые точки

 1. Из уравнений (1), (2) вытекает очевидное следствие

                                                      

дающее первый интеграл исходной системы

                                                                                                                                                (7)

Поэтому, для исследования поведения интегральных кривых системы (4)–(6) достаточно исключить из нее переменную  E.

 2. При  системе (4), (5) соответствует уравнение фазовых траекторий

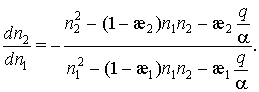                                                               (8)

При  из уравнений (4), (5) вытекает алгебраическая система

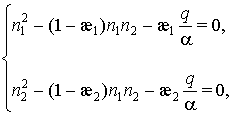                                                                     (9)

определяющая особые точки уравнения (8), расположенные в конечной части фазовой плоскости .

 3. При 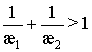 системе (9) удовлетворяют координаты только следующих пар точек

                

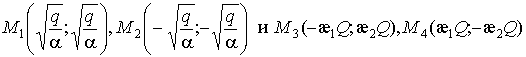
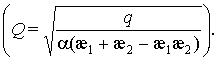
В случае 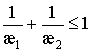 особыми в конечной части плоскости остаются только точки , .

 4. Характеристическое уравнение, соответствующее особой точке , имеет вид

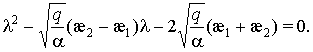                                                   (10)

Свободный член (10) отрицателен, собственные числа  действительные и разных знаков. Поскольку поле направлений, задаваемое уравнением (8), симметрично относительно начала координат, особые точки  и  – седла. Характеристическое уравнение, соответствующее точке , имеет вид

          (11)

дискриминант которого

                          

Свободный член (11) при условии 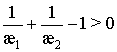 положителен, собственные числа  действительные и одного знака. В силу упомянутой симметрии поля направлений, задаваемого уравнением (8), особые точки  и  – узлы.

5. В конечной части плоскости  отсутствуют замкнутые траектории (в том числе и предельные циклы) уравнения (8), так как нет других особых точек, кроме узлов и седел, а к узлам примыкает интегральная (вытекает из (7)) прямая .

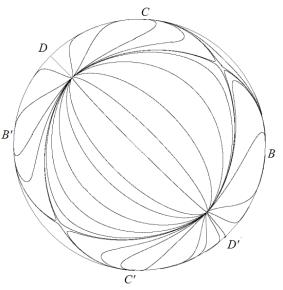
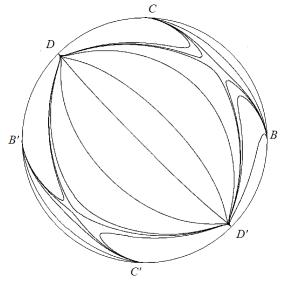
Поведение траекторий уравнения (8) на фазовой плоскости  представлено на рис. 1, 2.

Рис. 1

Рис. 2

 

Поведение траекторий на бесконечности

Исследуются бесконечно удаленные особые точки уравнения (8).

1. Первое преобразование Пуанкаре [6]

                                      

приводит к уравнению

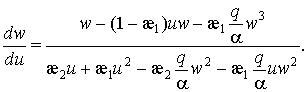                                                   (12)

При  (12) имеет две особые точки  и 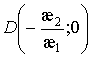. Особая точка  B при любых значения параметров суть узел. Особая точка  D при 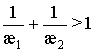 является седлом, а при 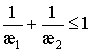 – узлом. Экватор сферы Пуанкаре (соответствует оси ) состоит из траекторий уравнения.

2. Второе преобразование Пуанкаре

                                      

приводит к уравнению

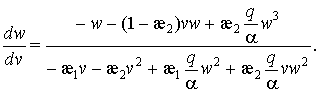                                                 (13)

Особая точка  для (13) при любых рассматриваемых значениях параметров является узлом.

3. Поведение траекторий уравнения (8) на "круге Пуанкаре" с 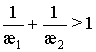случае  характеризует картина, представленная на рис. 1, а в случае 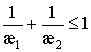 – на рис. 2.

4. Таким образом, качественные свойства решений исходной трехмерной математической модели (1)–(3) полностью определяются первым интегралом (7) и фазовым портретом на круге Пуанкаре (рис. 1, 2).

 

Список использованной литературы

1.     Thomson J.A. Conduction of electricity through gases. Cambridge: Univ. Press, 1903.

2.     Swan W. The atmospheric potential gradient and a theory as to the cause of its connection with others phenomena in atmosphere electricity, together with certain conclusions as to expression for the electric force between two parallel charged plates // Terr. Magn. Atmos. Elec. 1913. V. 18. Р. 163–164.

3.     Chalmers J.A. The theory of electrode effect // J. Atm. Terr. Phys. 1966. V. 28. 565–579.

4.     Hoppel W.A. Electrode effect: comparison of the theory and measurement. Pianetary Electrodynamics: Gordon and Beach Sci. Publ. 1969. P. 167–181.

5.     Терентьев А.М. Аналитическое и качественное решение классической задачи электродного эффекта // Вестник ННГУ им. Н.И. Лобачевского. 2011. № 4 (1). С. 146–148.

6.     Андронов А.А., Леонтович Е.А., Гордон И.И., Майер А.Г. Качественная теория динамических систем. М.: Наука, 1966.

© А.М. Терентьев, 2016