УДК 624. 01(02)

Ж.Б. Байнатов (проф.), С.Е. Нұразхан (магистрант)

(Казахский национальный исследовательский технический

университет имени К. И. Сатпаева,

Республика Казахстан, г. Алматы, wrts.nur@gmail.com)

Трансформируемая конструкция покрытия трибуны стадиона

Аннотация. Предлагаемая статья посвящена одной из наиболее быстро прогрессирующих областей современного строительства пространственного покрытия спортивных сооружений. Основной задачей при реконструкции существующих стадионов является решение покрытия трибуны. На сегодня 95% стадионов Казахстана не имеют хотя бы частичного покрытия. Возможно покрытие части трибун центрального стадиона в Алматы не является рациональным т.к. покрытия осуществляется частично и он не эффективно защищает трибуны от атмосферных воздействий. Кроме того консольный вариант несущих элементов покрытия уязвимы к сейсмическим воздействиям.

Ключевые слова: Шпренгельная балка, трехшарнирная арка, покрытия, трибуны, трансформируемые панели

 Annotation. This article is dedicated to one of the most rapidly progressing areas of modern construction of the spatial coverage of sports facilities. The main task of the reconstruction of the existing stadium is the solution to cover the stands. At present, 95% of Kazakhstan's stadiums are not at least a partial coating. Perhaps part of the cover of the central stadium in Almaty stands is not rational because the coating is carried out in part and it does not effectively protect the rostrum weatherproof. In addition the console version of the bearing elements covering vulnerable to seismic shocks.

Keywords: Truss beams, threehinge arch, cover, the rostrum,
transformable panels

Для покрытия больших площадей часто применяются вантовые системы. В вантовых системах элементы перекрытий – балки, фермы, складки, оболочки и т.п. подвешиваются к стальным канатам – вантам, передающим их воздействия на опоры. Однако вантовые и висячие системы перекрытий не всегда являются рациональным в основном из-за гибкости, использовать их в сейсмоопасных регионах не желательно.

Компоновка конструкций больших площадей выгодно осуществить из комбинированных конструкций, при этом надо учесть, что такие конструкций работают в основном на нагрузки от собственного веса, поэтому уменьшение собственного веса конструкций является главной задачей конструктора. С этой точки зрения рациональным вариантом является применение в большепролетных конструкциях стали повышенных прочности или легких сплавов как материалов, из которых можно изготовить самые легкие конструкций. Малый объемный вес алюминиевых сплавов при большой их прочности делает их весьма перспективными в качестве материала для несущих конструкций большепролетных зданий.

Нами предлагается для перекрытия открытых стадионов, конструкций большепролетных комбинированных арочных систем, которые расчленяются на отдельные плоские конструктивные элементы (арки, главные балки прогоны и т.п.), которые рассчитываются обычными методами строительной механики.

В нашем варианте перекрытии основными несущими конструкциями являются арки (Рис1.)

а)

б)

в)

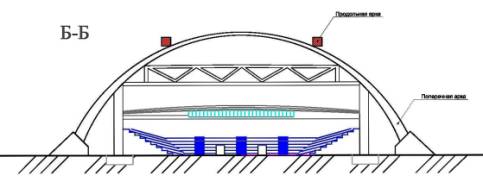
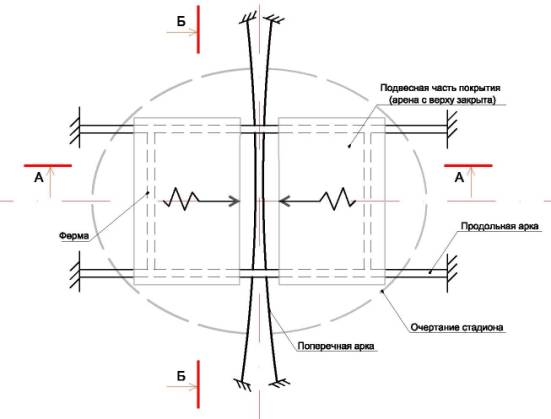
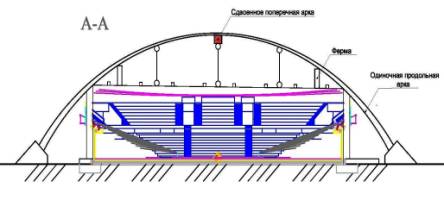
Рис-1. Общий вид плана покрытия и разрезы стадиона

а)- Схематичный план стадиона с трансформируемым покрытием (закрытое состояние);

б)- продольный разрез по А-А;

в)- поперечный разрез по Б-Б (другие составляющие элементы не показаны).

а)

б)

в)

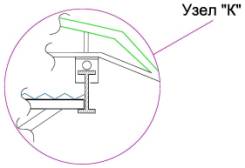
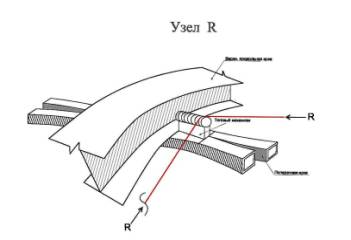
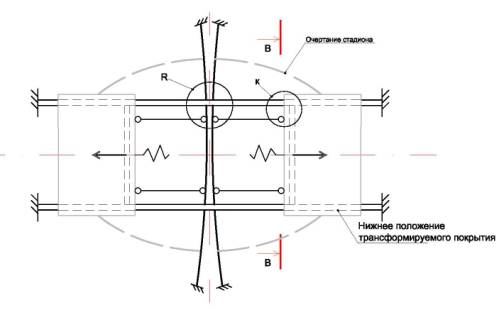
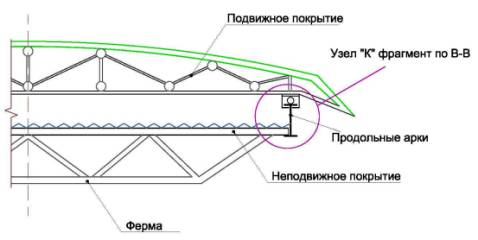
Рис-2. Общий вид плана покрытия стадиона и узлы;

а)- план стадиона с трансформируемым покрытием (открытое состояние);

б)- Узел и фрагменты расположения несущих элементов.

Особенность этого решения состоит в том, что по двум продольным аркам перемещаются панели покрытия то удаляясь то приближаясь друг к другу. Перемещение панели покрытия осуществляется цилиндрическим катком, размещенные на верхней полке продольных арок. Движение при вытягиваний или отпускание осуществляется электродвигателями размещенные на поясе поперечной арки. Разветвлёнными опорным частям.

При открытом положений покрытия стадиона трансформируемые панели будут расположены над торцевыми покрытиями.

Как показано на (Рис 1а) две, трех шарнирные арки расположены над беговой дорожкой вдоль стадиона, а третья сдвоенная трехшарнирная арка расположена в середине стадиона поперек двум продольным аркам. Кроме того а этой поперечной арке опираются продольные арки, в результате образуются пространственная перекрестная несущая система.

Продольные арки имеют высокое расположение и жесткие затяжки на подвесках для опирения главных балок перекрытия трибуны. К двум продольным аркам установлены трансформируемая часть перекрытий, причем они при необходимости закрываются приближаясь и состыкуясь с поперечной аркой, а при открытий удаляются от поперечной арки в сторону футбольного ворота.

Применение трехшарнирной арочной системы с затяжкой позволяет расчленять конструкцию на отправочные элементы, удобные по условиям перевозки и монтажа. Затяжка может использоваться для устройства подвесного потолка.

При расчете арки основным вопросом является поиск оптимального очертание и сечения оси арки.

Рассмотрим следующие два случая загружения арки:

1. Арка находится под действием сплошной равномерно распределённой нагрузки (Рис 2а). За начало координат примем левый опорный шарнир. Дифференциальное уравнение оси напишем так:

После двукратного интегрирования получим выражение ординат оси арки:

Входящие в него постоянные С₁ и С₂ определяются из условий:

при х=0 у=0 С₂=0

х=L₁ y'=0 C₁= L₁

В соответствии с этим уравнение ординат оси напишется так:

(1)

Следовательно, при действии сплошной вертикальной равномерно распределенной нагрузки рациональная ось арки очерчивается по параболе.

а) б)

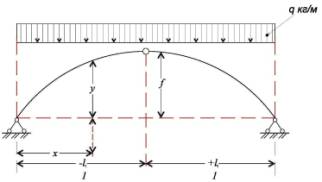
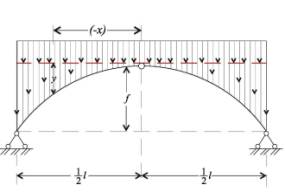
Рис-3а. Схемы загружения трехшарнирной арки.

а) - равномерно распределенная нагрузка;

б) – нагрузки с учетом (кармана) скопления.

2. Арка находится под действием вертикальной сплошной нагрузки, нарастающей соответственно очертанию оси арки. Такая схема загружения возможно когда сложная крыша полностью занесена снегом. (Рис -2а. б)). В этом случае нагрузка на каждый элемент арки определяется величиной

где γ – удельный вес нагрузки над осью арки. Приняв за начало координат средний шарнир на вершине арки, напишем дифференциальное уравнение оси арки:

Обозначив 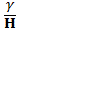через k², получим:

Так как правая часть этого уравнения – величина постоянная, то из решения этого дифференциального уравнения получим уравнение ординат оси арки

Входящие в это уравнение постоянные А₁ и А₂ определяются из условий:

при х=0 у=0, a потому

х=0 y'=0 А₁= 0

Таким образом уравнение рациональной оси при нагрузке указанного вида (Рис-3б) будет:

(2)

Это уравнение носит название катеноида Легея (Legay). Для определения величины входящего в это уравнение распора Н следует использовать условие положения пятовых шарниров, т.е. что при x= 0,5 l, y=f :

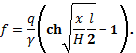
Для более удобного вычисления ординат Штрасснер (Strassner) преобразовал уравнение Легея. Он обозначил отношение нагрузки на опоре q_s к нагрузке в ключе q

Отсюда получаем:

Обозначив отношение через , получим уравнение катеноида по Штрасснеру (118):

(3)

В котором

Для облегчения вычисления ординат по этому уравнению пользуются специальными таблицами.[4]

ЛИТЕРАТУРА

1. Снитко Н.К. Строительная механика. –М.: Высшая школа, — 529 с.

2. С. И. Вайдман, Л. Ф. Теверовский, Д. В. Яковлев. Строительные конструкции. — Ленинград: Издательство литературы по строительству, — 344 с.

3. Строительные пространственные конструкции: учебное пособие / Н.В. Канчели. М. : АСВ, 2003. 112 с

4. Каменцев и Дучинский, Бесшарнирные арочные мосты

5. www.archi-dizain.blogspot.com