УДК 539.376

А.Г. ТАМРАЗЯН, д-р техн. наук, академик РИА, профессор (МГСУ), (Россия)

Д.Г. КЛЕКЧЯН, канд. техн. наук (ЕАСГУ), (Республика Армения)

О теории вязко-упруго-пластичности бетона

Многочисленные эксперименты показали, что упругость для бетона приемлема до определенного предела нормальных напряжений . О.Я. Берг[1], анализируя известные опытные данные, пришел к выводу, что когда , то отклонение связи – от прямолинейности настолько значительно, что недопустимо игнорирование пластичной сущности деформационного процесса бетонной среды, как при мгновенном, так и при длительном воздействии внешне-силовых факторов. Параметр определяет как границу упругости и пластичности, так и линейной и нелинейной ползучести бетона. Численное значение этого коэффициента, как считал О.Я. Берг, находится в пределах .

И так, при и если значение со временем остается постоянной, деформация будет меняться по закономерности

, (1)

где –некоторая функция от напряжения, выражающая нелинейную связь (пластичность) между напряжением и деформацией, –модуль упругости стареющего со временем материала (бетона), величина которой, соответственно к набиранию прочности (взрослению бетона), растет, –мера ползучести бетона, –момент приложения внешнесиловых воздействий.

Если со временем напряжение меняет свою величину, связь – будет выражаться интегродифференциальным уравнением

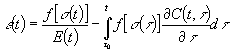. (2)

Очевидно, что (2) значительно отличается от уравнения нелинейной ползучести предложенной Н.Х. Арутюняном([2], стр. 291, формула (8.7)):

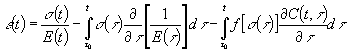. (3)

Разница между (2) и (3) имеет принципиальное значение для теории как нелинейной, так и линейной ползучести бетона (линейная ползучесть характеризуется подстановкой в (1)–(3) ) и в своей основе имеет следующее объяснение. При постоянных напряжениях связь – Н.Х. Арутюняном представляется так([2], стр. 290, формула (8.2)):

. (4)

Влияние только ползучести на деформацию должно выражаться через и никак иначе. Влияние на деформацию роста со временем к ползучести никакого отношения не имеет и необходимо это влияние выражать совершенно автономно. Очевидно, что в (4) изменение деформации, вызванное изменением со временем полностью игнорируется и в итоге вся эволюция деформации приписывается вязкости среды. В результате формула (4) дает искаженную картину ползучести.

Второе существенное отличие между (1) и (4) заключается в том, что (1) отражает истинную картину деформационного состояния бетона, поскольку нелинейность ползучести именно вызвана пластическим состоянием материала при . По (4) получается, что под данным напряжением бетон работает упругомгновенно, а ползучесть нелинейна. Это, конечно, искажает сущность нелинейности ползучести, поскольку нелинейную ползучесть вызвана именно пластическим состоянием среды.

В результате все это приводит к существенной разнице между уравнениями (2) и (3).

Мера ползучести имеет следующие характерные особенности.

а). с ростом растет, но с монотонно убывающей скоростью:

, если .

Этим отражается экспериментально установленным фактом, что даже при нелинейной ползучести деформация ползучести бетона имеет затухающую природу.

б). с ростом монотонно убывает, следовательно отрицательная функция. Это является следствием факта спада свойства ползучести с ростом .

Аналитическая функция меры ползучести должна отражать как вязкостную природу бетона, так и его взросление. В обабщенном виде эту функцию можно представить формулой

, (5)

где через –выражается влияние возраста бетона при его загружении, а через –влияние текучего времени, т.е. времени, при котором определяется значение деформации ползучести.

Из обобщенной формулы (6) можно получить любые комбинации аналитических функций меры ползучести. Например,

– мера ползучести теории наследственности[4]:

, (6)

, (7)

– мера ползучести реологической модели теории старения[4]:

, (8)

, (9)

– мера ползучести С.Г. Есаяна[4]

, (10)

, (11)

– мера ползучести Н.Х. Арутюняна[2]

, (12)

, (13)

– мера ползучести С.В. Александровского([3] :

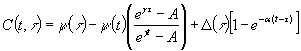, (14)

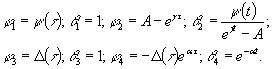(15)

Условие б) означает

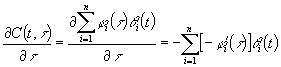. (16)

Поскольку , то: .

Интегральное уравнение

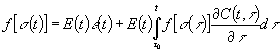(17)

по существу является интегральным уравнением Вольтерра второго рода по отношению к , если считать известной функцией.

Если требуется определить закономерность изменения , то необходимо, во- первых, иметь функцию в явном виде и, во- вторых, используя граничные условия и условие равновесия, найти вторую связь между напряжением и деформацией[4]:

, (18)

где параметр определяется из условий равновесия и совместности деформаций.

Подставив (18) в (17) и учитывая (16), получим

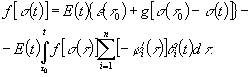(19)

Решение интегрального уравнения (19) проведем методом разложения неизвестной функции в степенной ряд по степеням

, (20)

, (21)

где некоторый положительный параметр.

Коэффициенты ряда (21) определяются через используя правила дифференцирования сложной функции:

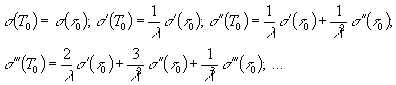(22)

Коэффициенты определяются поочередным дифференцированием интегрального уравнения (19) и подстановкой в полученных выражениях .

Очевидно, что если значение параметра определить по формуле

. (23)

то третий член ряда (21) превращается в ноль, что значительно актививизирует сходимость ряда и, как показывают многочисленные сравнительные расчеты, уже первые два члена с требуемой точностью дают решение задачи

. (24)

При необходимости, подставляя (24) в (19) и проведя интегрирование, находим второе приближение и т.д.

Пример. Требуется определить закономерность релаксации напряжений в бетонном стержне с учетом нелинейной ползучести. Т.е. необходимо получить ту закономерность спада напряжений , которая обеспечит условие . Поскольку по условию задачи требуется определение только с учетом нелинейной ползучести, то тогда, исключая влияние изменения на процесс (т.е. принимая ), исходное интегральное уравнение получит вид:

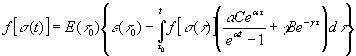. (25)

Дважды дифференцируя (25) по и подставляя получим значения и :

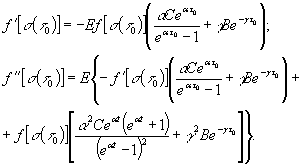(26)

Подставив (26) в (23) и (24) получим значение . Для определения необходимо иметь аналитический вид функции напряжения. Допустим

, (27)

где опытный параметр. Тогда необходимая закономерность изменения будет

. (28)

Библиографический список

1.Берг О.Я. Физические основы теории прочности бетона и железобетона.–М.: Стройздат,1961.-96 с.

2.Арутюнян Н.Х. Некоторые вопросы теории ползучести. –М.: Гостехиздат, 1952. –324 с.

3.Александровский С.В. Расчет бетонных и железобетонных конструкций на изменение температуры и влажности с учетом ползучести. –М.: Стройиздат, 1973. –432 с.

4.Есаян С.Г. Реологическое моделирование вязкоупругих, упругопластических и вязкоупругопластических сред. –Ереван, Чартарагет, 209, –368 с.