Аппроксимация таблично-графически заданных функций

Данилов А.М., д.т.н. проф., Гарькина И.А., д.т.н. проф.

Пензенский государственный университет архитектуры и строительства

Рассмотрим функцию , заданную таблично-графически на прямоугольнике (конечным набором графиков, выражающих зависимость функции от первой переменной при каждом из заданных значений второй переменной ). Займемся ее аппроксимацией полиномом

Для этого воспользуемся асимптотическими полиномами, которые применялись в [1] для аппроксимации функции на отрезке

,

где , (); символ означает: ; () – полиномы Чебышева первого рода: - точки, асимптотически близкие при к точкам альтернанса (точки, в которых разность непрерывной функции и ее полинома наилучшего приближения данной степени достигает поочередно значений , где - наилучшее приближение полиномами ).

Справедливо:

, .

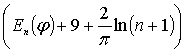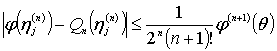
При аппроксимации (ограничимся полиномами степени ) функции двух переменных воспользуемся последовательной аппроксимацией асимптотическим полиномом по каждой из двух переменных (в итоге и получим требуемый вид асимптотического полинома от двух переменных).

Введем

; ;

при имеем .

После замены переменных получим .

Задача сведется к аппроксимации заданной таблично-графически функции (заданы графики функций , ). Впредь вместо используется обозначение (,, ). В дальнейшем необходимы значения , . Заданные значения (), вообще говоря, не совпадают с (). Если и точки эквидистантны, то достаточно удалить , тогда , ,,. В остальных случаях значения можно определить приближенно в виде

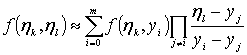
(интерполяционный полином Лагранжа степени ). Конечно, это неизбежно несколько снизит точность окончательного результата.

При каждом фиксированном значении получим аппроксимацию

,

где , ().

В свою очередь, при каждом получим аппроксимацию

,

где , ().

В итоге приходим к аппроксимации, где

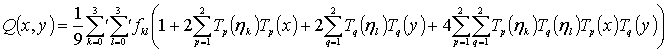Здесь , ; ,, .

После приведения подобных членов будем иметь:

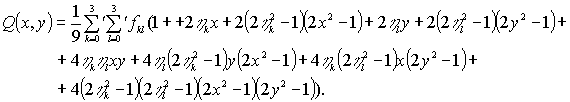
Таким образом, функция на прямоугольнике аппроксимируется асимптотическим полиномом от двух переменных

.

Коэффициенты () есть суммы произведений элементов матрицы на соответствующие элементы матриц , а именно: ,,, , ,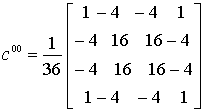

, , .

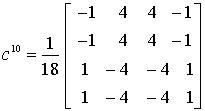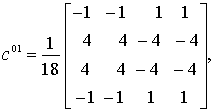
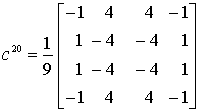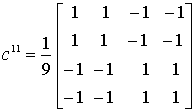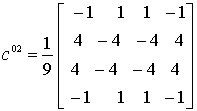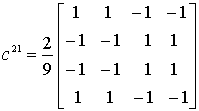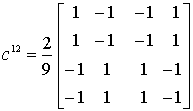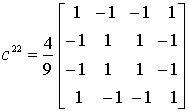Вернувшись к исходным переменным , окончательно получим аппроксимирующий заданную функцию на прямоугольнике асимптотический полином от двух переменных

; .

Подчеркнем, что гораздо целесообразнее оставить этот полином расположенным по степеням . Представление

требует вычисления новых коэффициентов :

,

,

,

,

,

,

,

,

,

что связано с неизбежным накоплением новых погрешностей.

Если среди значений , при которых заданы графики зависимости функции от , нет хотя бы некоторых из значений , то повышение степени аппроксимирующего полинома сверх , вообще говоря, лишь усложняет вычисления, но не увеличивает точность аппроксимации. Поэтому сделанный нами выбор аппроксимирующего полинома степени предполагает, что .

Литература

1. Этерман И.И. Аппроксимация функций асимптотическими полиномами /И.И.Этерман // Известия ВУЗов. Математика. – 1962. - №6. – С.162-171.