Шилинец В. А., Горавская Н. Г.
Белорусский государственный педагогический университет
РЕШЕНИЕ ОДНОЙ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МЕТОДАМИ F–МОНОГЕННЫХ ФУНКЦИЙ
Как известно,
дифференциальные операторы (формальные производные)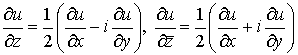 
использовались рядом
авторов при исследовании уравнений в частных производных. В частности, И.Н.
Векуа [1] успешно применял эти операторы для исследования дифференциального
уравнения
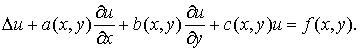
Целью данного
исследования является решение с помощью функций, моногенных в смысле В. С.
Фёдорова (F-моногенных) [2,3], следующей системы
дифференциальных уравнений в формальных производных 
(1)
где 
––действительные или комплексные константы;
––односвязная область плоскости 
; 
––искомые комплексные функции класса
. Считаем 
.
Введем замену 
, тогда система (1) примет вид:
(2)
где 
––некоторые постоянные, 
Если положить 
, то система (2) редуцируется к виду
(3)
где 
.
Пусть 
1
и 
2
–– корни уравнения
(4)
Из (3),
очевидно, следует:
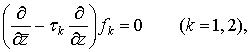(5)
где 
.
1o.
––
действительные. Полагаем 
Имеем 
Вводим
формальные производные [4]
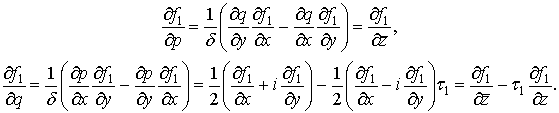
Уравнение (5)
для 
примет вид 
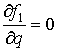, откуда делаем вывод, что 
––любая F–моногенная по функции 
функция.
Аналогично: 
––любая F–моногенная по функции 
в области 
функция. Из равенств 
, 
находим 
и 
.
2о. 
––комплексные.
Положим 
, 
. Имеем 
Вводим
формальные производные
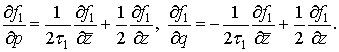
Легко видеть,
что
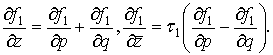
Отсюда следует,
что уравнение (5) при 
равносильно уравнению
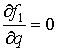, а потому получим, что 
–– F–моногенная
по функции 
функция. Аналогично:
––функция, F–моногенная по функции 
. Далее находим 
и 
.
3о. 
Имеем 
, причем 
. Отсюда 
Первое уравнение
системы (3) примет вид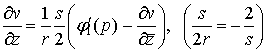 
; 
Отсюда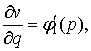 
а потому 
где 
––любая F–моногенная по 
функция.
Задача решается
формулами 
и 
.
Литература
1.
Векуа И. Н. Обобщенные
аналитические функции.– М.:ГИФМЛ, 1959.–628 с.
2.
Фёдоров В.С. Основные
свойства обобщенных моногенных функций // Известия вузов. Математика, 1958. – №
6. – С. 257-265.
3.
Стельмашук Н.Т., Шилинец
В.А. О преобразовании к каноническому виду системы линейных уравнений в частных
производных с помощью двойных дифференциальных операторов // Весці НАН Беларусі. Сер.
фіз.-мат. навук, 2008. – № 2. – С. 61-65.
4.
Гусев В.А. Об одном
обобщении ареолярных производных // Bul. Stiint. si tehnical inst. Pol. Timisoara, 1962. – T. 7, fasc. 2. – P. 223-238.