К.т.н. Макаренко Н.Б.

Днепропетровский национальный университет, Украина

Идентификация областей дефектов в тонкостенных телах

Проблема технической диагностики состоит в идентификации физических и геометрических параметров реальной системы с помощью измерений откликов исследуемой системы на внешнее воздействие. Решение такой задачи связано с получением обратного оператора для краевой задачи теории упругости, что приводит при численной реализации к непреодолимым трудностям, определяемым, в первую очередь, плохой обусловленностью задачи. Известные методы регуляризации, используемые непосредственно при решении вариационной задачи, трудоемки и малоэффективны при решении высокоразмерных задач, какими являются задачи теории упругости для неоднородных или поврежденных систем. Кроме того, указанные решения не дают информации об эффективных точках сравнения (точки, где проводятся измерения) и наиболее информативных параметрах модели.

Предлагается идентифицировать параметры повреждений в результате решения обратной задачи, принимая во внимание данные косвенных измерений.

Рассматривается система, функция состояния которой в ограниченной пространственной области где – вектор пространственных координат, определяется соотношениями

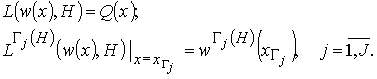(1)

Здесь – вектор функций состояния (перемещений), – внутренние и граничные контуры области , , – заданные дифференциальные операторы, H – функции, характеризующие повреждения или дефекты. Кроме того, задана вектор-функция и её значения , которые определяются путем косвенных измерений. Необходимо при заданных определить значения функций H так, чтобы удовлетворялось условие

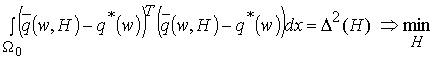
(2)

либо

где – значения вектор-функции, полученные в результате решения задачи (1). Для решения прямой задачи (1) вводится сетка с координатами узлов и соответствующими значениями функции ; для дискретного описания вектор-функции в точках наблюдения вводится сетка с координатами узлов из числа (R – область определения) и значениями функции ; описание параметров модели j-го дефекта (повреждения) осуществляется введением логической функции в зависимости от его вида как описание замкнутой границы области дефекта , на которой заданы соответствующие граничные условия: а) свободного края (при сквозном повреждении или трещине), при этом область пуста ; б) совместности перемещений и деформаций границы области дефекта и соответствующей границы неповрежденной части области , при изменении распределенных свойств системы, например, характерного размера или модуля упругости, определяемых компонентами вектора H (). 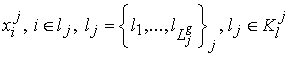Дискретизация границы задается замкнутой ломаной линией с координатами узлов , где – число узлов ломаной, – область определения векторов . Вектор определим как вектор параметров, описывающих границу области в виде , область зададим значениями компонентов вектора , где – значения соответствующих t-тых параметров дефекта внутри области . Отметим, что для сквозного повреждения . При этом предполагается, что область дискретизирована с помощью сетки с координатами узлов где – множество узлов сетки , находящихся внутри и на границе области . Условия (2) в дискретной постановке приобретают вид:

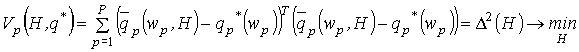(3)

или . (4)

Решение уравнения (4) включает в себя выбор оптимальной аппроксимации границы , т.е. выбор числа вершин ломаной и набора , описывающих границу дефекта, выбор наиболее информативных наблюдений из числа P возможных с номерами точек сравнения , где – область определения векторов , и определение вектора H.

Для решения уравнений (4) используем алгоритм метода Ньютона:

, (5)

где n – номер итерации или наблюдения (индекс g опущен). Для построения матрицы А используется матрица чувствительности 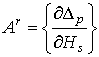, где p, s – соответственно номера точек измерений () и номера компонентов вектора H, определяемые множеством возможных параметров модели повреждения (). Число , соответствующее количеству точек сравнения, выбранных из возможно измеряемых, и равное числу неизвестных компонентов вектора H, должно удовлетворять условию , т.к. в общем случае матрица плохо обусловлена и возможно выполнение условия , где – размерность матрицы чувствительности. Так как критерий (4) задан неявно, то матрица может быть построена численно с помощью разностного аналога 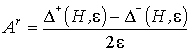, где Δ⁺(H,e)={Δ(H+e×e₁),…, Δ(H+e×e_p)}, Δ^–(H,e)={Δ(H–e×e₁),…, Δ(H–e×e_p)}; e – малое приращение; e_j – базисные векторы: e₁=(1,0,…,0); e₂=(0,1,…,0); …; e_p=(0,0,…,1). Соотношение (5) в виде системы линейных уравнений относительно – вектора приращений на n-м шаге вычислений

. (6)

Таким образом, оказывается возможным применение идентификационно-инверсного метода [1], с помощью которого и были проведены расчеты. Было установлено, что при наличии близко расположенных дефектов их идентификацию удается провести только путем специального подбора значения или получая огибающую области дефекта.

Литература:

1. Ободан Н.И., Макаренко Н.Б. Идентификационно-инверсный метод диагностики повреждений // Зб. наук. праць “Методи розв’язування прикладних задач механіки деформівного твердого тіла”.– Наука і освіта.– Дніпропетровськ.– 2006.– №7.– С. 81–88.