Гавеля Г.М.

Днепропетровский национальный университет, Украина

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ТОНКИХ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ПРИ НАЛИЧИИ ОДНОСТОРОННИХ УПРУГИХ СВЯЗЕЙ

Определение условий образования локальной или регулярной форм потери устойчивости тонких панелей при односторонних связях имеет прикладное значение. Такая постановка задачи представлена в литературе [1–3], однако указанная постановка позволяет установить возможность потери устойчивости в виде регулярной формы. Но при некоторых значениях параметров системы тонкая оболочка стремится образовать одну большую складку как более энергетически выгодную. Исследовать указанные типы поведения системы возможно только при изучении нелинейного поведения оболочки или панели при наличии односторонних связей.

Деформированное состояние цилиндрической панели под действием внеш-него давления описывается системой нелинейных уравнений изгиба срединной поверхности цилиндрической оболочки.

Отрицательные радиальные прогибы панели не должны превышать зазор между панелью и жестким основанием

, (1)

где – безразмерные радиальное перемещение и зазор, – толщина панели.

Предполагается, что в процессе деформирования возникают зоны прилегания панели к основанию и отставания. Угловая координата границы зоны контакта предполагается переменной. На границе зоны контакта и в области контакта должны выполняться условия для радиальных прогибов

, (2)

где – угол полураствора панели.

Условия совместности усилий и деформаций должны выполняться на границе зоны контакта .

Сформулированная нелинейная краевая задача решается вариационным методом. Вариационная задача, эквивалентная исходной, формулируется как задача стационарности функционала , состоящего из потенциальной энергии деформации участков отставания и прилегания, потенциала внешних сил, функционала присоединенных условий совместности деформаций и присоединенных условий (2) с помощью множителей Лагранжа.

Выполняя условие стационарности функционала , можно определить систему разрешающих уравнений, при этом выполняются условия (2), условия совместности силовых компонент и условия трансверсальности

(3)

на границе зоны контакта панели с основанием.

Для перехода от двухмерной вариационной задачи к одномерной применяется метод разделения переменных. Искомые функции выбираются в виде, который учитывает характер изменяемости решения ( аналогично исследованию цилиндрических оболочек в жесткой обойме) [4]: в виде рядов, удовлетворяющих условию шарнирного опирания на контурах :

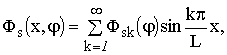(4)

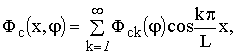(5)

где , – безразмерные функции, которые описывают - мембранные усилия; - изгибающие и крутящий моменты; - перерезывающие силы; - внешнее давление; - перемещения; - углы поворота нормали; - безразмерный параметр; - радиус и длина панели; - продольная и окружная координаты; - модуль упругости и коэффициент Пуассона; .

При подстановке искомых функций в виде (4) – (5) в условие стационарности (с учетом только первой гармоники, так как ее вклад для прогиба составляет около 90%) можно получить систем разрешающих уравнений по координате и граничные условия в точке .

Для решения этой задачи используется метод перехода к эквивалентной задаче Коши. При этом задается начальный вектор , в который входят значения функций задачи в точке и величины контактного давления и подвижной границы зоны контакта , которые должны обеспечивать выполнение системы дифференциальных уравнений и граничные условия на продольных кромках панели.

Интегрирование задачи Коши с начальным вектором , осуществляемое с помощью метода Рунге-Кутта, дает вектор невязок краевых условий, соотношений (2) и условия стационарности функционала. Для реализации процесса минимизации вектора невязок используется метод Ньютона, в котором невязки включены в вектор-функцию .

Итерационный процесс метода Ньютона для выполнения условия ,

изложен в [5].

В качестве начального выбирается вектор , первый элемент которого соответствует заданной нагрузке, то есть равномерно - распределенному сжимающему давлению . В зависимости от граничных условий на продольных кромках элементам и ставятся в соответствие те независимые функции, характеризирующие напряженно-деформированное состояние, которые не входят в граничные условия. Например, если на продольных кромках закрепление в виде неподвижного шарнира), то элементом является продольное перемещение , – усилие , – перерезывающая сила , – угол поворота . В качестве последнего элемента вектора выбирается наиболее быстроизменяющаяся функция. Обычно в подобных задачах в качестве выбирается радиальное перемещение , но в данной задаче значение задано на границе. Неизвестное значение скачка перерезывающей силы помещается в , а значение подвижной зоны контакта – в .

Так как рассматривается симметричная в тангенциальном направлении форма деформирования, то в вектор невязок входят условия в точке контакта :,,–и условия симметрии в середине панели :

Для построения закритических решений регулярного или локального типа используется метод возмущений, который состоит в выборе начального возмущения в виде предполагаемого решения. Для выхода на закритическое состояние значению угла зоны контакта присваивается постоянное значение, то есть закрепляется зона контакта, а в качестве элемента выбирается значение возмущающего давления , действующего на участках и .По мере увеличения давления возмущающее давление растет, а когда форма деформирования панели приближается к закритической, уменьшается до нуля. При в элементе значение возмущения заменяется значением угла зоны контакта , то есть зона контакта становится подвижной.

В процессе поиска решения используется метод движения по параметру [5], причем организуются два вложенных процесса – движение по основному нагружению ( ведущий параметр или ) и движение по параметру .

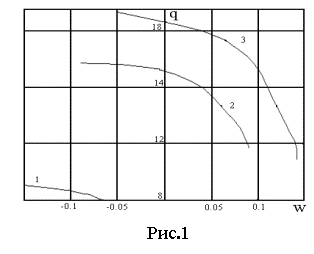
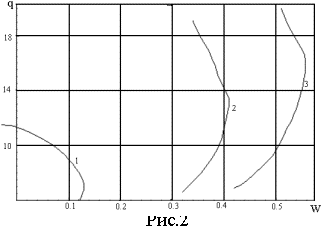
Характерная картина закритических решений и формы изгиба панели , находящейся под действием равномерного внешнего давления , приведена на рис.1 (угол раствора панели ), и рис.2 ( угол раствора панели ). На обоих рисунках кривая 1 соответствует зазору , кривая 2 – , кривая 3 – . Давление на графиках отнесено к величине критического давления для нестесненной цилиндрической оболочки, через обозначен безразмерный радиальный прогиб в точке .

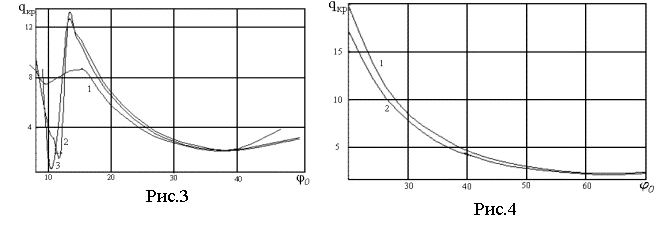
На рис.3 и рис.4 приведены зависимости критических значений давления от угла раствора панели. При малых углах раствора зависимость носит осциллирующий характер, причем значение давления может изменяться в широком диапазоне, форма закритического деформирования соответствует образованию локальной формы. При увеличении угла раствора уровень критических значений давления изменяется монотонно, достигая минимального значения при с последующим плавным увеличением. Аналогичная картина наблюдается и в случае оболочки – тонкий слой деформируется с образованием мелких вмятин, причем их число, соответствующее минимальной критической нагрузке, равно числу волн, образующихся при потере устойчивости цилиндрической однослойной оболочки.

На основе численных расчетов следует отметить:

· критическая нагрузка монотонно убывает при увеличении угла раствора для панелей с ;

· критическая нагрузка значительно зависит от величины зазора лишь для узких панелей.

Литература:

1. Нелинейное деформирование цилиндрической оболочки с наведенной неоднородностью материала, контактирующего с неоднородным основанием // Иноземцев В.К., Конусевич В.И., Синева Н.Ф., Фролов Э.П. Прочность материалов и конструкций, взаимодействующих с агрессивными средами. Саратов: Изд-во Саратов. гос. техн. ун-та.1998. С. 89–92.

2. Георгиевский В.П., Тарасова А.Г. Устойчивость ортотропной цилиндрической оболочки с заполнителем при действии внешнего давления // Изд-во РАН. Механика твердого тела. 2001. № 1. С. 167–173.

3. Naili S., Odlou C. Buckling of a short cylindrical shell surrounded by an elastic medium // Trans. ASME J. Appl. Mech. 2000. Vol. 67, № 1. P. 212–214.

4. Ободан Н.И., Железко И.П., Гавеля Г.М. Поведение цилиндрической оболочки в жесткой обойме при внешнем давлении // Прикл. механика.– 1997.– Т. 33, №4.– С.48 – 53.

5. Андреев Л.В.,Ободан Н.И., Лебедев А.Г. Устойчивость оболочек при неосесимметричной деформации. М., 1988. 208 с.