Биологические науки/

11.биоинженерия и биоинформатика

К.т.н. Ростовцев В.С., аспирант Новокшонов Е.В.

Вятский государственный университет, Россия

Теорема дедукции в терминах ДНК-вычислений

1 Логическое следствие и теорема дедукции

Пусть дано множество формул:

(1)

и формула G. Говорят что G есть логическое следствие формул (1) (или G логически следует из (1), тогда и только тогда, когда для всякой интерпретации, при которой одновременно истинны все формулы (1), формула G так же истинна. Формулы (1) называют посылками, а формулу G логическим следствием или заключением.

В дедуктивных системах необходимо доказать, что некоторая формула логически следует из других формул. Обычно, утверждение, что формула логически следует из формул, называют теоремой. Проблема поиска решений сводится к проблеме доказательства теоремы. То есть построения рассуждения, устанавливающего, что формула логически следует из других формул.

Теорема дедукции. Пусть даны формулы (1) и формула G. G есть логическое следствие (1) тогда и только тогда, когда общезначима любая из равносильных формул:

, (2)

(3)

Теорема о противоречии. Пусть даны формулы (1) и формула G. G есть логическое следствие посылок (1) тогда и только тогда, когда противоречива любая из равносильных формул:

, (4)

(5)

Эти две теоремы имеют важное значение – они позволяют прийти к выводу что доказательство того, что отдельная формула есть логическое следствие конечного множества формул, эквивалентно доказательству того, что некоторая связанная с ними формула общезначима или противоречива. Таким образом, доказательство того, что данная формула G является логическим следствием конечной последовательности формул (1), сводится к доказательству общезначимости формул (2) или (3), или доказательству противоречивости формул (4) или (5) Поэтому, многие задачи могут быть сформулированы как проблемы доказательства теорем [1].

Стоит отметить, что из двух теорем, на практике чаще применяется теорема о противоречии. То есть для доказательства того что формула G является логическим следствием формул (1), ставится задача доказать противоречивость формул (4) или (5). Так как в формулах заключение теоремы опровергается, то и процедуры поиска доказательства называются процедурами поиска опровержения.

3.1.2 Пример вывода

Пусть целью вывода служит формула F. Множество посылок содержит известный факт B и базу знаний из семи формул в базисе : ; ; ; ; ; .

Для указанной постановки задачи формулы теорем (3) и (5) имеют вид:

(6)

и

(7)

После раскрытия скобок и приведения к нормальной форме формулы (6) имеем эквивалентную формулу:

. (8)

В формулах (6) - (8) используется шесть переменных, таким образом, всего существует 2⁶ = 64 различных интерпретации. Несложно доказать общезначимость формул (6) и (8) и противоречивость формулы (7) простым перебором всех возможных интерпретаций.

2 Метод Липтона

ДНК-алгоритм для решения задачи о выполнимости логической формулы был предложен Ричардом Липтоном в работе [2]. Работы Липтона [2, 3] опираются на модель ДНК-вычислений [4], разработанную Леонардом Эдлманом и использованную в его знаменитом эксперименте [5]. Модификация метода, позволяющая использовать его для доказательства теоремы дедукции и организации на основе этой теоремы логического вывода, предложена в [6].

2.1 Описание метода

Липтон сформулировал свой алгоритм для решения классической задачи выполнимости формулы (SAT) [2], по формулировке которой формула представлена в конъюнктивной нормальной форме (КНФ):

(9)

где

. (10)

Дизъюнкции называются множителями КНФ, число множителей k называется длиной формулы, количество слагаемых называют рангом дизъюнкции. В случае k=0 КНФ называется пустой и считается равной 0 (ЛОЖЬ). Общее число литералов или, что то же самое, сумма рангов дизъюнкций, входящих в КНФ, называется сложностью КНФ.

По аналогии с оригинальным ДНК-алгоритмом Липтона можно построить алгоритм, определяющий выполнимость формулы, представленной в дизъюнктивной нормальной форме (ДНФ):

(11)

где

. (12)

Метод Липтона состоит из четырех этапов:

· Этап №1 – построение графа литералов G;

· Этап №2 – кодирование графа G и получение всех возможных путей по методу Эдлмана;

· Этап №3 – применение к полученным путям фильтрующих процедур;

· Этап №4 – анализ результата фильтрации и интерпретация решения;

Далее приведено подробное описание этапов на примере формулы (8).

Вначале строится направленный граф G состоящий из 3n+1вершины. В графе 2n вершин представляют положительные и отрицательные литералы всех n атомов формулы, остальные n+1 вершины промежуточные. В множестве промежуточных вершин выделяют начальную и конечную вершины. Любая промежуточная вершина, кроме начальной и конечной, имеет две входящие и две исходящие дуги. Начальной вершине инцидентны только исходящие дуги, а конечной только входящие. Дуги графа соединяют между собой только литеральные вершины и промежуточные. Пара дуг, исходящих или входящих в промежуточную вершину соединяет её с парой вершин, соответствующих контрарным литералам одного атома. Граф для формулы (8), построенный по описанным выше правилам, представлен на рисунке 1, где vs – начальная вершина, vk – конечная, vi – прочие промежуточные вершины.

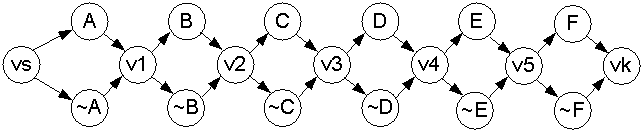Рисунок 1 – Граф литералов формулы (8)

Общее количество вершин такого графа определяется формулой:

(13)

а общее количество дуг:

(14)

Для каждой из промежуточных вершин существует ровно два варианта продолжения пути, и эти варианты не зависят друг от друга. Таки образом, из вершины vs в вершину vk проходит ровно 2ⁿ путей. Между множеством путей графа G и множеством интерпретаций формулы (8) существует естественное взаимно однозначное соответствие. Например, путь vs-a-v1-b-v2-c-v3-d-v4-e-v5-f-vk соответствует интерпретации, при которой все переменные принимают значение ИСТИНА.

Вершины и дуги графа кодируются точно так же как в эксперименте Эдлмана [5] Каждая i-я вершина кодируется произвольной последовательностью s_i длиной LEN(s_i) нуклеотидов. Обычно, удобно использовать четное значение LEN(s_i). Если LEN(s_i) – четное, то можно представить код вершины в виде конкатенации двух равных по длине строк s_i¹ и s_i²: s_i = s_i¹s_i². Каждая дуга соединяющая вершины s_i и s_j, кодируется последовательностью e_i,j = h(s_i², s_j¹), где h(a,b) морфизм Уотсона-Крика. Заключительная часть второго этапа, а так же третий и четвертый этапы в методе Липтона реализуются последовательностью ДНК-операций – ДНК-алгоритмом.

Первый шаг алгоритма выполняется так же, как и в опыте Эдлмана. В пробирку N помещается большое количество цепочек кодирующих каждую вершину и каждое ребро графа G. Далее выполняется сшивка цепочек. В процессе ренатурации коды s_i служат скрепками, благодаря которым сшиваются олигонуклеотиды, соответствующие смежным ребрам e_k,i и e_i,j. После ренатурации пробирка N содержит двойные цепочки ДНК, кодирующие произвольные пути в G. Таким образом, кодируются все возможные интерпретации n атомов исходной формулы.

Этап фильтрации представляет собой последовательность фильтрующих операций, которые должны выделить из всего множества возможных интерпретаций формулы те, на которых формула принимает значение ИСТИНА. Данный этап значительной степени зависит от конкретной записи исходной формулы. В качестве процедуры поиска используется операция выделения цепочки по заданному суффиксу. В качестве иллюстрации запишем второй этап алгоритма Липтона для формулы (8) на языке DNACL при следующих обозначениях:

· _N – пробирка, содержащая только двойные цепочки правильных (существующих в G) путей в графе;

· _A, _neA, _B, _neB, …, _F, _neF – переменные, хранящие коды вершин A, ~A, B, ~B и так далее.

Формула (8) записана в ДНФ, следовательно, она принимает значение ИСТИНА когда истинна хотя бы одна любая элементарная конъюнкция. Простейший случай элементарной конъюнкции – отдельный литерал. В формулы (8) присутствует два таких слагаемых: и . Для того, чтобы выделить в графе пути, содержащие вершины и выполняется фильтрацию по кодам этих вершин:

_N1=RS(_N, _F); // выделение интерпретаций содержащих F

_N2=RS(_N, _neB); // выделение интерпретаций содержащих ~B

После выполнение этих двух операций пробирка _N1 содержит цепочки, кодирующие все пути, проходящие через вершину F, то есть все интерпретации, в которых принимает значение ИСТИНА. Пробирка _N2 содержит все интерпретации, в которых (8) принимает значение ЛОЖЬ. Таким образом, после объединения этих пробирок _Nout=UNION(_N1, _N2) результирующая пробирка _Nout будет хранить коды 48 интерпретаций, на которых формула (8) принимает значение ИСТИНА. Причем, кодовые цепочки интерпретаций, содержащих одновременно и , и будут иметь удвоенную кратность по сравнению с прочими.

Остальные слагаемые формулы (8) состоят из двух литералов, поэтому фильтрация выделяющая соответствующие интерпретации, выполняется в два этапа. Для того чтобы конъюнкция приняла значение ИСТИНА необходимо что бы все её сомножители были истинны. Таким образом, для выделения интерпретаций, обращающих в ИСТИНУ первую конъюнкцию формулы (8) необходимо провести фильтрацию по коду вершины , а затем полученный результат ещё раз отфильтровать по коду вершины :

_N1=RS(_N, _A); // выделение интерпретацийD содержащих A

_N1=RS(_N1, _neF); // выделение интерпретацийD содержащих A и ~F.

После выполнение этих двух операций пробирка _N1 содержит цепочки, кодирующие все интерпретации, в которых A принимает значение ИСТИНА и F принимает значение ЛОЖЬ. Если сейчас объединить _N1 с пробиркой результата _Nout, то к результату будут добавлены коды восьми новых интерпретаций, обращающих формулу (8) в истину, и увеличены кратности 24 кодов интерпретаций, полученных на предыдущих шагах фильтрации. Аналогично выполняется фильтрация для всех остальных слагаемых формулы.

Последний этап метода Липтона (и ДНК-алгоритма) заключается в проверке наличия в результирующей пробирке цепочек. Если после завершения всех шагов фильтрации и объединения их результатов в пробирке _Nout присутствует хотя бы одна цепочка, то формула выполнима. Проверку наличия цепочек _Nout в пробирке можно осуществить с помощью операции.

Для того чтобы доказать теорему дедукции необходимо показать что формула (8) не только выполнима в некоторых интерпретациях, но и является тавтологией, то есть, выполнима при любом наборе значений атомов. Если формула является тавтологией пробирка результата должна содержать все возможные пути графа или, что то же самое, быть равной как минимум по составу исходной пробирке _N. Сравнение двух пробирок исключительно по составу, то есть без учета кратностей цепочек, выполняет операция CMPSN. Предложенная в [6] модификация позволяет использовать метод Липтона для доказательства общезначимости формул, и как следствие, для организации логического вывода на основе теорем дедукции и противоречия.

Таким образом, алгоритм Липтона может быть использован для решения задач о выполнимости и общезначимости формул вида (9) и (11), а так же для организации дедуктивного логического вывода. Отрицательный результат операции NOTNULL означает невыполнимость формулы и доказывает теорему противоречия. Положительный результат операций NOTNULL означает выполнимость формулы, а положительный результат операции CMPSN означает, что формула является общезначимой и доказывает теорему дедукции.

2.2 Достоинства метода

Наиболее важное достоинство, описанного ДНК-алгоритма, – это массовый параллелизм обработки информации, основанный на свойствах ДНК-цепочек. Лучше всего возможность массовой параллельной обработки информации с помощью ДНК-операций иллюстрирует первый шаг алгоритма. Все возможные пути в графе (интерпретации формулы) строятся с помощью выполнения одной единственной ДНК-операции RENAT. На последующих шагах алгоритма массовый параллелизм проявляется не так явно как на первом, хотя и здесь он позволяет значительно сократить количество операций. Оценить сложность решения задачи в ДНК-операциях можно следующим образом.

Если формула представлена в КНФ вида (9), то для решения задачи о её выполнимости или общезначимости потребуется одна операция RENAT для формирования интерпретаций, одна операция NOTNULL, если проверяется выполнимость формулы или одна операция CMPSN, если проверяется общезначимость. Кроме того, для фильтрации по каждому литералу a_i,j каждого дизъюнкта C_j вида (10) потребуется l_j операций RS и l_j−1 операций UNION для формирования результата фильтрации по дизъюнкту C_j. Таким образом, общее число ДНК-операций в алгоритме Липтона для решения задачи о выполнимости или общезначимости формулы в КНФ, равно:

. (15)

Аналогично, если формула представлена в ДНФ вида (11), то для решения задачи о её выполнимости или общезначимости потребуется одна операция RENATN, одна операция NOTNULL или CMPSND для фильтрации по каждому литералу b_i,j каждой элементарной конъюнкции Q_j вида (12) потребуется t_i операций RS. Для объединения результатов фильтрации по отдельным конъюнкциям в одну пробирку потребуется m − 1 операций UNION. Таким образом, общее число ДНК-операций в алгоритме Липтона для решения задачи о выполнимости или общезначимости формулы в ДНФ равно:

. (16)

Слагаемые и представляют собой суммы рангов всех элементарных дизъюнкций КНФ и конъюнкций ДНФ, то есть равны сложности формул. Таким образом, в обоих случаях количество ДНК-операций, необходимое для решения NP-полной задачи о выполнимости формулы, линейно зависит от её сложности.

Как уже отмечалось, массовая параллельная обработка опирается на свойства ДНК-цепочек. При фильтрации естественный параллелизм обработки ДНК проявляется в значительно меньшей степени. Причина этого кроется в способе построения фильтрующий процедур – последовательность фильтраций определяется непосредственно записью формулы. Кроме того, при определении набора фильтрующих процедур не учитываются зависимости между подформулами. С другой стороны, используемые в методе Липтона правила построения фильтрующих процедур обуславливают наличие в ДНК-алгоритме скрытого параллелизма другого рода. Анализ нормальных форм и правил построения по ним фильтрующих процедур выявил возможность выполнения нескольких фильтрующих процедур параллельно.

Любое слагаемое дизъюнкции, принимающее значение ИСТИНА, обращает в истину всю дизъюнкцию. Поэтому, можно выполнять фильтрацию по каждому слагаемому дизъюнкции (10) или (11) независимо от других. Таким образом, фильтрация дизъюнкции может быть представлена множеством параллельных процедур фильтрации, каждая из которых выделяет интерпретации, обращающие в ИСТИНУ одно из слагаемых. Все параллельные фильтрации по отдельным слагаемым выполняются над одной и той же пробиркой. В случае обработки формул вида (11) исходной пробиркой для параллельных процедур фильтрации является начальная пробирка, хранящая все интерпретации формулы. При обработке формул (10) исходная пробирка для группы процедур, выполняющих фильтрацию, формируется в результате фильтрации предыдущих сомножителей КНФ: C₁, C₂, … , C_i−1. Результатом фильтрации по всему дизъюнкту является пробирка, объединяющая результаты фильтраций по отдельным слагаемым.

Независимыми друг от друга являются только слагаемые в пределах одного дизъюнкта. Поэтому, размер элементарного процесса зависит от размера слагаемых. Таким образом, зернистость подзадачи фильтрации в значительной степени определяется формой формулы КНФ или ДНФ. Размер элементарного процесса в процедуре фильтрации КНФ, вне зависимости от сложности формулы, равен ровно одной ДНК-операции. При обработке формул в ДНФ размер элементарного процесса не фиксирован. Минимальный размер элементарного процесса – одна ДНК-операция в случае, если в формуле одно из слагаемых представляет собой литерал. Максимальный размер элементарного процесса – n ДНК-операций, может иметь место при обработке ДНФ, одно или несколько слагаемых которой имеют ранг n.

К достоинствам метода следует отнести и тот факт, что граф, по которому производится кодирование интерпретаций, зависит не от исходной формулы, а только от числа входящих в неё атомов. Таким образом, для решения задачи о выполнимости или общезначимости любой формулы, зависящей не более чем от n атомов, можно использовать один и тот же граф из K_V1=3n+1 вершин и K_U1 = 4n ребер. Это означает, что решение для всех указанных формул можно начинать с одной и той же пробирки.

Значительно упрощает процесс организации вычислений тот факт, что алгоритм Липтона использует небольшой набор операций: ренатурацию, фильтрацию пробирки по заданному суффиксу, объединение пробирок и проверку наличия цепочек в пробирке. Для организации доказательства теоремы дедукции на основе указанного алгоритма требуется всего одна дополнительная операция сравнение пробирок по составу. Ограниченный набор используемых ДНК-операций, а так же регулярность структур входных формул (9) и (11) позволяют достаточно просто автоматизировать процесс построения ДНК-программы (последовательности ДНК-операций), проверяющей выполнимость и\или общезначимость формулы. Схемы алгоритмов для построения последовательности ДНК-операций, выполняющих проверку выполнимости и общезначимости формул в ДНФ и КНФ представлены на рисунках 2 и 3. Исходными данными для алгоритмов генерации ДНК-программ служат:

· n – количество атомов в формуле;

· k – количество множителей в КНФ;

· t[i] – количество слагаемых в i-м множителей КНФ;

· m – количество слагаемых в ДНФ;

· l[i] –количество множителей в i-м слагаемом ДНФ;

· c_X[i,j] – константа-строка (цепочка), кодирующая j-й множитель (j-е слагаемое) i-м слагаемом (i-м множителе) ДНФ (КНФ);

В ДНК-программах используются следующие переменные:

· _N – пробирка, содержащая коды вершин и ребер графа;

· _Nout – пробирка с результатом фильтраций;

· _N_i – пробирки для промежуточных результатов фильтрации, для обработки ДНФ требуется только одна пробирка для промежуточных результатов, для обработки КНФ требуется max(t[i]) временных пробирок.

Схемы алгоритмов, представленные на рисунках 2 и 3, предназначены для составления ДНК-программ на языке DNACL, однако, они применимы для любой модели ДНК-вычислений, в которой над пробирками определены такие команды модели параллельной фильтрации как ренатурация, выделение по суффиксу, объединение, обнаружение и сравнение по составу.

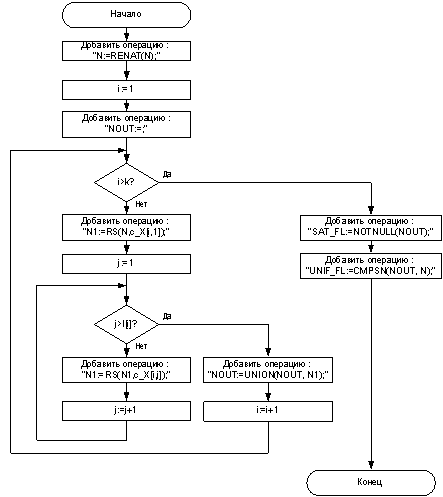
Рисунок 2 – Схема алгоритма создания ДНК-программы для обработки ДНФ

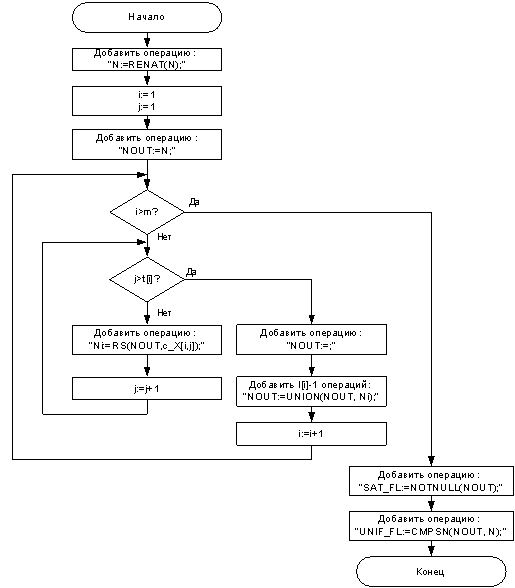
Рисунок 3 – Алгоритм создания ДНК-программы для обработки КНФ

Кроме формул с регулярной структурой (ДНФ и КНФ) метод Липтона так же способен обрабатывать и формулы произвольного вида [2]. Единственное обязательное требование к виду формулы – формула не должна содержать отрицаний, кроме отрицаний атомов. В этом смысле метод является достаточно универсальным и не требует приведения исходной формулы к регулярному виду. В связи с тем, что произвольная формула имеет иррегулярную структуру при решение задачи о её выполнимости применяется другой способ построения графа литералов. Граф литералов в этом случае строится в два этапа. Сначала по формуле строится контактная схема [7], а затем контактная схема преобразуется в направленный граф G. В отличие от графа литералов регулярных формул, в графе, построенном на основе контактной схемы, отсутствуют промежуточные вершины, кроме начальной и конечной. Например, контактная схема формулы будет иметь вид, представленный на рисунке 4, а граф литералов, построенный по указанной контактной схеме, приведен на рисунке 5.

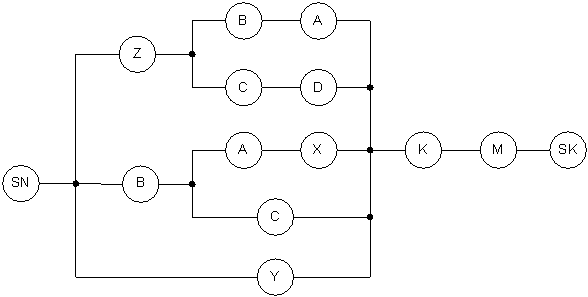
Рисунок 4 – Контактная схема

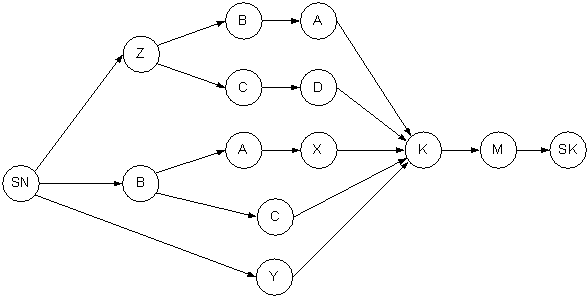
Рисунок 5 – Граф литералов

Остальные этапы метода Липтона при обработке произвольной формулы выполняются точно так же как и при обработке нормальных форм. Как показано в [2] сложность (в смысле количества ДНК-операций) задачи о выполнимости произвольной формулы линейно зависит от её размера. Стоит отметить, что отсутствие регулярной структуры формулы значительно усложняет анализ и автоматическую генерацию последовательности необходимых для решения задачи ДНК-операций.

2.3 Недостатки метода и пути их устранения

Кроме очевидных достоинств оригинальный метод Липтона имеет так же ряд недостатков, многие из которых могут быть устранены с помощью современных достижений области ДНК-вычислений.

Один из основных недостатков метода заключается в том, что ДНК-программа в значительной степени зависит от размера и строения обрабатываемой формулы, особенно, при обработке иррегулярных формул. Это относится, в первую очередь, к наиболее трудоемкому этапу фильтрации. В частности, количество фильтрующих ДНК-операций равно количеству литералов в формуле. Значение второго аргумента функции (суффиксов по которым производится фильтрация) каждой фильтрующей операции определяется литералом в заданной позиции формулы. На практике такой подход требует подготовки множества сайтов узнавания и организации специальных процедур разделения по указанным сайтам. Последовательность применения фильтрующий и объединяющий операций зависит от структуры формулы. Так же от структуры формулы зависят все аргументы операций UNION и первые аргументы (пробирки, которые подвергаются фильтрации) фильтрующих операций. Таким образом, каждый раз для решения задачи о выполнимости или общезначимости некоторой формулы требует составления специфичной для этой формулы ДНК-программы.

Целая группа сложностей при использовании метода обусловлена слабой проработкой вопросов кодирования графа литералов. Единственное требование к кодированию вершин и ребер графа описанное в методе: коды всех вершин и ребер графа должны быть уникальными. Можно выделить следующие слабые стороны кодирования в оригинальном методе Липтона.

Во-первых, сам граф литералов G избыточен. Промежуточные вершины в графе литералов, представленном на рисунке (1) являются искусственным дополнением собственно графа литералов. С точки зрения логики высказываний, комбинаторики и парадигмы ДНК-вычислений промежуточные вершины, кроме начальной и конечной, не выполняют какой-либо функции при построении путей в графе G. Граф литералов почти на треть (n-1 из 3n+1 вершин) состоит из таких бесполезных промежуточных вершин. При этом, промежуточные вершины должны быть закодированы и их коды должны быть помещены в исходную пробирку наравне с кодами литеральных вершин. Таким образом, наличие промежуточных вершин значительно увеличивает необходимое количество исходного генетического материала. Устранить данный недостаток можно путем исключения промежуточных вершин. Естественно, удаление промежуточных вершин следует производить с сохранением общего числа путей между вершинами vs и vk, а так же соответствия между путями в графе интерпретациями формулы. Например, модифицированный граф литералов для формулы (8) представлен на рисунке 6. Общее количество дуг графа по-прежнему определяется выражением (14), а количество вершин уменьшилось, почти на треть:

. (17)

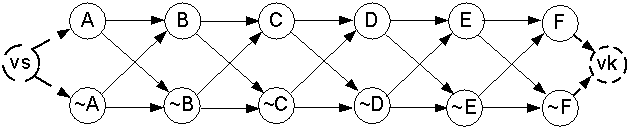
Рисунок 6 – Модифицированный граф литералов формулы (8)

Вторая проблема, вызванная произвольным кодированием вершин и ребер, заключается в том, что подобное кодирование может стать причиной ошибок различных типов. Влияние некоторых из них можно нивелировать непосредственно на этапе выполнения операций с помощью настройки макропараметров операций, таких как концентрации (кратность цепочек в пробирке) и температуры.

Например, ошибки типа “ложное срабатывание” (false positives) [8, 9] часто представляют собой результат непредусмотренных планом эксперимента сшивок. Так как вторичные структуры, образованные в результате ренатурации, не полностью комплементарных кодов, менее стабильны чем полностью комплементарные двойные цепочки, то первые могут быть разрушены с помощью увеличения температуры. Настройка концентрации цепочек в исходном генетическом материале может значительно сократить вероятность появления части ошибок типа “ложное срабатывание”.

С другой стороны, настройка макропараметров для каждой ДНК-операции достаточно сложная и трудоемкая процедура. Кроме того, только настойкой температуры и кратности невозможно исключить все ошибки появляющиеся в следствии произвольного кодирования.

Пример плохого кодирования вызывающего ошибки, которые нельзя исключить настройкой макропараметров, приведен на рисунке 7. Граф (сплошные линии) состоит из четырех вершин V1, V2, V3 и V4, и соединяющих их трех ребер U12, U23, U34. Используются коды вершин и ребер длиной в шесть нуклеотидов.

Из-за плохого подбора кодов, при построении всех возможных путей возможна генерация ложных путей с несуществующими ребрами U14, U31 и U11. В этой ситуации уменьшение концентрации кодов вершин V1, V3 и V4, участвующих в образовании ложных путей, несколько уменьшает вероятность ошибок типа “ложное срабатывание", но при этом увеличивается вероятность того что правильные пути (без несуществующих ребер) не будут построены. Увеличение температуры так же не может предотвратить образование (в динамическом смысле) или разрушить уже образовавшиеся ложные пути.

Рисунок 3.7 – Пример неудачного кодирования вершин и ребер

Причина заключается в том, что в двойной цепочке пара нуклеотидов G-C имеет три водородные связи, в то время как пара A-T только две. Стабильность участка двойной цепочки, который образуется при взаимодействии кодов вершины V1 и ребра U34 составляет не менее 0,86 от значения стабильности соединения кодов вершины V3 и ребра U34 и, как минимум, не меньше чем стабильность участка двойной ДНК на стыке U23 и V3. Поэтому, увеличение температуры раствора, достаточное для разрушения нежелательных участков двойной ДНК, в большой долей вероятности приведет к разрушению правильных путей.

Как показано ранее, недостаточная проработка вопросов кодирования может стать причиной большого числа различных ошибок при выполнении ДНК-операций. В худшем случае, наличие ошибок может привести к неудаче всего эксперимента с генетическим материалом. Нивелирование же массы разнотипных ошибок значительно усложняет реализацию, как отдельных этапов, так и всего эксперимента в целом. Построение эффективных методов кодирования исходных данных задачи в терминах ДНК-цепочек, основанных на свойствах используемого ДНК-алгоритма и генетического материала, имеет таким образом, огромное значение. Эффективный метод, гарантирующий качественное кодирование, не только упрощает выполнение ДНК-программы, но так же упрощает и ускоряет этап подготовки исходного материала.

Обычно, способ кодирования исходных данных в терминах ДНК-операций и\или последовательностей нуклеотидов является неотъемлемой частью ДНК-алгоритма [10]. Однако, некоторые методы вычислений оговаривают только минимально необходимые требования к кодам для предания им определенных свойств и допускают различные варианты кодирования. Липтон в своей работе [2] описал два основных (обязательных) требования к кодам вершин и ребер графа. Во-первых, коды вершин и ребер должны быть уникальны, и, во-вторых, код ребра должен содержать две подцепочки, каждая из которых должна быть комплементарна части кода одной из инцидентных этому ребру вершин. Эти два ограничения, накладываемые на коды вершин и ребер являются необходимыми для выполнения ДНК-алгоритма, но как показано выше этих ограничений не всегда достаточно, для безошибочного и быстрого выполнения операций его составляющих.

Анализ алгоритма, типов возможных ошибок и причин их возникновения оказывает, что многие проблемы оригинального метода могут быть решены на этапе подготовки генетического материала. В частности, может быть полезно наложение следующих дополнительных ограничений на кодирование графа:

· длина кода должна быть минимальной;

· код вершины должен содержать четное число нуклеотидов;

· код вершины должен иметь регулярную структуру;

· любая пара кодовых цепочек (вершина-вершина, вершина-ребро или ребро-ребро) не должна образовывать устойчивую вторичную ДНК-структуру без липких концов, то есть ни один из кодов не может являться полным дополнением другого кода или самого себя;

· коды вершин и ребер должны быть построены таким образом, что бы не допустить образование из двух любых кодов вершин (ребер) двойных цепочек с липкими концами;

· кодирование должно исключать возможность выполнения сшивок, непредусмотренных алгоритмом или, как минимум, гарантировать, что их результаты будут значительно менее стабильными, чем вторичные структуры, образование которых предусмотрено методом.

Для предотвращения ложных срабатываний можно применить способ, используемый в [11] для разделения посылок и заключений в импликативных правилах. Способ заключается в выделении в коде вершины (ребра) двух областей: информационной и вспомогательной (служебной). Основная функция информационной части кода –идентификация кодируемого объекта. Уникальность всего кода объекта обеспечивается уникальностью его информационной части. Коды без явного выделения информационной и служебной частей можно считать частным случаем с пустой служебной частью. Служебная область используется для придания коду специфических свойств. При кодировании графа для метода Липтона на служебную область кодирующей цепочки возлагается функция предотвращения “ложных срабатываний”. При построении путей в графе не предусмотренные алгоритмом сшивки кодов вершин и ребер происходят, в основном, по причине взаимодействия меньших, чем это предусмотрено алгоритмом, участков кодирующих цепочек. Поэтому, целесообразно разместить на обоих концах кодов вершин и ребер нуклеотидные последовательности, которые бы увеличивали стабильность правильных вторичных структур (образованных полностью комплементарными и определенной длины подцепочками кодов вершин и ребер) и одновременно снижали бы стабильность неправильных.

Еще один прием, который можно использовать для придания ДНК-коду определенных свойств – ограничение алфавита информационной части кода. С одной стороны, редукция алфавита уменьшает информационную емкость кодовой позиции и, как следствие, приводит к увеличению длины информационной части. С другой, за счет использования отработанных приемов построения кодов в бинарном алфавите позволяет значительно упростить и автоматизировать процесс формирования информационной части ДНК-кода. Кроме того, не используемые в информационной части кода символы могут быть использованы в служебной. Таким образом, достигается, во-первых, наглядность разделения информационной и служебной частей, а, во-вторых, во многих случаях правильный выбор множества информационных символов значительно упрощает и формирование служебной части кода.

Применительно к кодированию графа может быть полезно следующее ограничение алфавита: информационная часть кода может содержать только символы A и T, а символы G и C предназначены для использования в служебной. Схема взаимодействия кодов вершины V_k и ребра U_pk представлено на рисунке 8. Служебная часть кодов выделена на рисунке цветом. Информационная часть каждого кода разделена на две части. В коде вершины Vk между двумя участками информационной части X₁X₂X_3···X_i и X_i+1X_i+2X_i+3···X_L расположена служебная последовательность нуклеотидов – "ответная" часть (GCGC) для служебных участков в начале и конце кодов двух инцидентных данной вершине ребер. Данная структура кодов практически исключает возможность образования не предусмотренных алгоритмом вторичных структур (путей в графе). В случае же образования таких не правильных путей, из-за своей нестабильности они могут быть легко разрушены незначительным изменением макропараметра – температуры. Однако, при таком кодировании теоретически возможно образование двойных цепочек с ровными концами. Данный вид вторичных структур, ни при каких обстоятельствах, не может быть интерпретирован как путь в графе. Поэтому наличие таких вторичных структур в результирующей пробирке не должно привести к искажению результата работы ДНК-алгоритма. С другой стороны, достаточно высокая вероятность образования таких вторичных структур, а так же их стабильность требуют значительного увеличения исходного генетического материала.

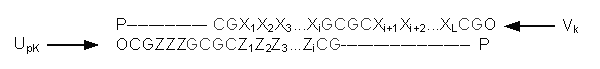
Рисунок 8 – Вторичная структура, образованная кодом ребра U_pk и вершины V_k

Для предотвращения образования вторичных структур с ровными концами можно использовать дополнительные ограничения на структуру информационной части кода: для любой пары кодов вершин или ребе α и β первая область (PX₁X₂X_3···X_iO) информационной части кода α не должна быть комплементарна второй области (PX_i+1X_i+2X_i+3···X_LO) информационной части кода β. Реализовать данное ограничение можно разными способами.

Например, можно сдвинуть ответную часть (GCGC) к одному из концов кодирующей цепочки. Данный сдвиг исключит симметрию размеров областей информационной части. Асимметрия размеров если и не исключит полностью возможность взаимодействия пары кодов вершин (ребер), то, как минимум, значительно уменьшит стабильность результата такого взаимодействия. Уменьшение стабильности, очевидно, будет пропорционально отношению длин областей информационной.

Однако у данного подхода есть принципиальный недостаток – асимметрия размеров областей информационной части повлечет так же изменение стабильности всех соединений между вершинами и ребрами в путях графа. Стабильность, примерно, половины соединений (вершина-ребро или ребро вершина в зависимости от направления сдвига) увеличится за счет увеличения размера взаимодействующих цепочек, а стабильность второй половины уменьшится по той же причине. Таким образом, любая двойная цепочка, кодирующая путь в графе, будет содержать в себе перемежающиеся области с повышенной и пониженной стабильностью. В этом случае использование увеличения температуры для уничтожения не предусмотренных алгоритмом сшивок является нежелательным, так как может привести к разрушению правильных путей в местах пониженной стабильности.

Существует и другой способ реализации указанного ограничения. Для предотвращения образования вторичных структур с ровными концами можно не разделять уникальный код информационной части на две области, а продублировать его и расположить ответную область служебной части между двух копий информационной. Схема взаимодействия кодов такого вида для вершины V_k и ребра U_pk представлено на рисунке 9.

Коды такого вида, практически, исключают образование двойных цепочек с ровными концами, при этом стабильность путей остается постоянной по всей длине двойной цепочки.

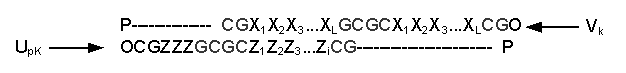
Рисунок 9 – Вторичная структура на стыке

модифицированных кодов ребра U_pk и вершины V_k

Для автоматизации кодирования графа удобно использовать в качестве идентификаторов вершин их номера. Нумерация вершин может быть выполнена в произвольном порядке, например, так как показано на рисунке 10. Нумерация позволяет в алгоритме генерации кодов представить граф в виде пары объектов: числа n - количество атомов в исходной формуле и списка ребер U.

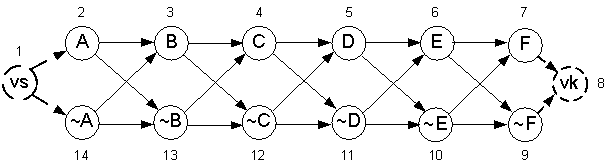
Рисунок 10 – Пример нумерации вершин графа.

Минимальный размер L информационной части (PX₁X₂X_3···X_LO) кода зависит от мощности используемого алфавита ss и количества вершин n. Минимальная длина информационной части равна:

, (18)

где ]x[ - результат округления до ближайшего большего целого, , N = 2n+2 по выражению (17) или N = 3n+1 по выражению (13). Таким образом, для графа, представленного на рисунке 8, имеются следующие исходные данные:

· n – количество атомов в формуле, равно 6;

· N=2n+2 – количество вершин в графе, равно 14;

· Q=4n – количество ребер в графе по выражению (14), равно 24;

· U[1..Q, 2] – список ребер: в U[i,1] хранится номер начальной вершины, в U[i,2] – номер конечной;

· L – минимальный размер информационной части по выражению (18), равен 4.

Сам алгоритм кодирования тривиален. Он основан на преобразовании номера вершины в двоичное представление и замене символов.

Использованные функции:

· Nto2(x) – возвращает строку двоичного представления целого числа x;

· H(w) – возвращает символ комплементарный по принципу Уотсона-Крика символу w, например, H(‘A’)=’T’;

· 2toDNA(s) – возвращает строку s, в которой символы ‘0’ и ‘1’ на ‘A’ и ‘T’.

Алгоритм:

1) Построить коды вершин:

1.1) Получить двоичное представление номеров вершин CVT[i]= Nto2(i), для всех .

1.2) Заменить символы ‘0’ и ‘1’ на ‘A’ и ‘T’ CVT[i]= 2toDNA(CVT[i]) , для всех .

1.3) Добавить служебную часть, продублировать информационную и указать направление химической связи: CV[i]=’CG’+ CVT[i]+’GCGC’ + CVT[i] +’CG’ , для всех .

1.4) Указать направление химической связи CV[i]=’P’+CV[i]+’O’.

2) Построить коды ребер, для всех :

2.1) Сформировать дополнение информационной части:

из кода начальной вершины: tmp1[j]=H(CVT[U[i,1]][j]), ;

и кода конечной вершины: tmp2[j]= H(CVT[U[i,2]][j]), ;

2.2) Добавить служебную часть и направление химической связи:

CU[i]=’OCG’+tmp1+’GCGC’+tmp2+’CGP’.

3) Конец

В результате работы такого алгоритма получаются:

· массив CV[1..N] содержит коды вершин с номерами от 1 до N;

· массив CU[1..Q] содержит коды ребер перечисленных в списке U.

Выводы

По сравнению с обработкой импликативных правил [11] дедуктивный логический вывод по методу Липтона имеет большую практическую ценность, так как он практически не накладывает ограничений на вид обрабатываемых формул.

Метод имеет ряд преимуществ веред другими способами организации ЛВ в парадигме ДНК-вычислений. Среди положительных черт метода стоит отметить универсальность представления всех формул с заданным числом литералов, линейную зависимость сложности вычислений (в ДНК-операциях) от сложности формул, использование массового параллелизма для решения NP-полной задачи построения множества путей в графе, простоту генерации ДНК-программ для формул с регулярной структурой (ДНФ и КНФ), а так же возможность модификации метода для обработки произвольных формул.

Наряду с достоинствами оригинальному методу и его расширению до теоремы присущ так же определенный перечень недостатков, связанных в основном со слабой проработкой вопросов кодирования графа литералов. При этом, стоит отметить, что на сегодняшний день, практически, все эти проблемы могут быть эффективно решены.

Литература:

1. Достоверный и правдоподобный вывод в интеллектуальных системах ‘Текст“ G В.Н. Вагин, Е.Ю. Головина, А.А.Загорянская, М.В.Фомина. – М.: Физматлит, 2004.

2. R.J. Lipton. Using dna to solve np-complete problems [Текст] / R.J.Lipton // Science._ 1995.- Vol. 268.

3. R.J.Lipton. Speeding up computations via molecular biology [Текст] / R.J.Lipton // DIMACS. Series in descret mathematics and theoretical computer science. Volume 27: DNA based Computers.- 1996. -Vol. 27.

4. L.M.Adleman. Computing with dna [Текст] / L.M.Adleman // Scienti-c American.- 1998.- no. 8.

5. L.M.Adleman. Molecular computation of solutions to combinatorial problems [Текст] / L.M.Adleman // Science.- 1994.- Vol. 226.

6. Д.В.Анисимов Решение проблемы дедукции с использованием свойств ДНК [Текст]/Д.В.Анисимов // Процессы управления и устойчивость: Труды 41-й международной научной конференции аспирантов и студентов / Под ред/ Н.В. Смирнова, Г.Ш. Тамасяна. – СПб: Издат. Дом С.-Петерб. ун-та, 2010.

7. М.А.Гаврилов Теория релейно-контактных схем. Анализ и синтез структуры релейно-контактных схем / М.А.Гаврилов.- М.: Издательство АН СССР, 1950.

8. R.J.Deaton Good encodings for dna-based solutions to combinatorial problems [Текст] / R.J.Deaton , J.Sager, D.Stefanovic // DNA Based Computers II, DIMACS Workshop 1996.- Vol. 44 of Series in Discrete Mathematics and Theoretical Computer Science.- NY.: American Mathematical Society, 1999.

9. J.Sager. Designing nucleotide sequences for computation: A survey of constraints [Текст] / J.Sager, D.Stefanovic // DNA Computing - 11th International Workshop on DNA Computing.- Vol. 3892 of Lecture Notes in Computer Science.- NY.: Springer, 2005.

10. В. С. Ростовцев. Моделирование ДНК-систем и их прикладное применение: учебное пособие [Текст] / В. С. Ростовцев. – Киров: Издательство ВятГУ, 2010.

11. В.С. Ростовцев Принципы кодирования и обработки импликативных правил на базе ДНК-цепочек / В.С. Ростовцев, Е.В. Новокшонов // Материалы VIII международной научно-практической конференции “ Перспективные разработки науки и техники-2012” –Przemyśl: Nauka i studia, 2012